Paraboloid
Inhalt dieser Webseite
Was ist ein Paraboloid?
Formel des Rotationsparaboloids
Volumen und Oberfläche
Graph mit Winplot
Elliptisches Paraboloid
Hyperbolisches Paraboloid		 Parabolkegel
Flächen zweiter Ordnung
Von der Parabel zum Paraboloid
Paraboloid im Internet
Referenzen
.
Zur Hauptseite    "Mathematische Basteleien"

Was ist ein Paraboloid?
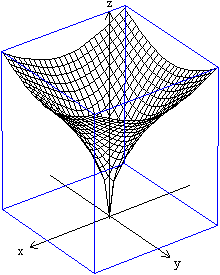
...... Im einfachsten Fall ist ein Paraboloid ein Rotationsparaboloid. 
Das ist der Körper, der entsteht, wenn eine Parabel im Raum um ihre Achse rotiert.

Dieses Paraboloid hat die Form eines unten runden Gefäßes, das oben keine Begrenzung hat.

Weiter unten werden noch das (allgemeinere) elliptische Paraboloid und das hyperbolische Paraboloid vorgestellt.

Formel des Rotationsparaboloids top
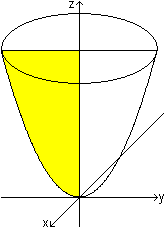...... Hat die erzeugende Parabel die Gleichung z=[1/(2p)]y² mit p>0, so hat das Paraboloid die Gleichung z=[1/(2p)](x²+y²).

Legt man eine Schnittebene senkrecht zur z-Achse, so ist die Schnittlinie ein Kreis.

Schließt man das Paraboloid oben mit diesem Kreis ab, dann stellt sich die Frage, wie groß das Volumen und die Mantelfläche dieses Körpers sind.

Volumen und Mantelfläche top
Rotiert eine Kurve mit y=f(x) um die x-Achse, so gelten für Volumen und Mantelfläche die beiden folgenden Formeln.

Volumen
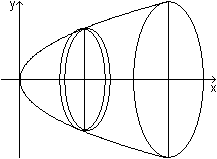...... Man stelle sich also vor, die Parabel mit y²=2px rotiere um die x-Achse. Dann gilt
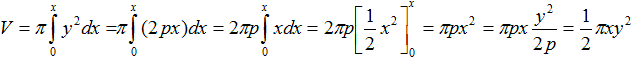Mantelfläche
Zur Berechnung des zweiten Integrals stellt man die Gleichung y²=2px, die Ableitung 2yy'= 2p oder y'=p/y und den Term sqrt(1+y'²)=sqrt(1+p²/y²)=(1/y)sqrt(2px+p²) bereit.
Das führt zu 

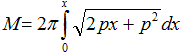
Substitution: z=sqrt(2px+p²)
Dann ist z²=2px+p² oder x=(z²-p²)/(2p) oder dx/dz=z/p oder dx=(1/p)zdz.
Weiter ist sqrt(2px+p²)dx gleich (1/p)z²dz. Das Integral kann berechnet werden:

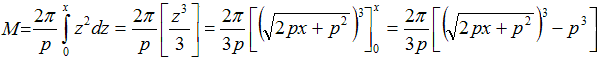
Ergebnis:

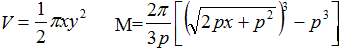
Graph mit Winplot   top
Das Zeichenprogramm Winplot stellt das Rotationsparaboloid mit Hilfe der Koordinatengleichung und einer  Parametergleichung wie folgt dar.

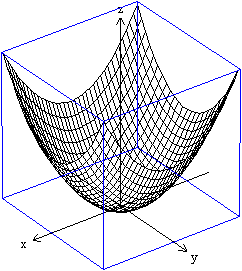
z=x²+y² mit -1<=x<=1 und -1<=y<=1

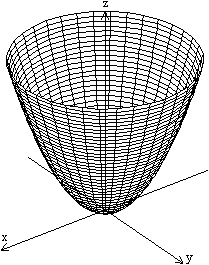
x=sqrt(u)cos(t), y=sqrt(u)sin(t), z=u 
mit 0<=t<=2pi, 0<=u<=pi

Parameter- und Koordinatendarstellung entsprechen sich:
x²+y²=[sqr(u)cos(t)]²+[sqr(u)sin(t)]²=u*cos²(t)+u*sin²(t)=u[sin²(t)+cos²(t)]=u=z, was zu zeigen war.
Auf meiner Seite Torus erkläre ich, wie man mit dem Freeware-Programm Winplot Körper dieser Art zeichnet. 

Elliptisches Paraboloid top
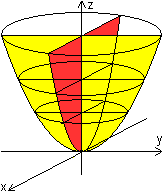...... Das Rotationsparaboloid wird durch die Gleichung z=[1/(2p)](x²+y²) oder z=x²/(2p)+y²/(2p) beschrieben.

Das elliptisches Paraboloid hat die leicht abgewandelte Gleichung z=x²/(2p)+y²/(2q), wobei p>0 und q>0 gilt. 

An Stelle der Kreise beim Rotationsparaboloid treten Ellipsen. In der z-x-Hauptebene liegt die Parabel z=x²/(2p) (rot gekennzeichnet) und in der z-y-Hauptebene die Parabel z=y²/(2q) (gelb gekennzeichnet).

Kurvenscharen
Die Gleichung des allgemeinen elliptischen Paraboloids lautet z=x²/(2p)+y²/(2q). 
Hält man eine Koordinate (rot) fest und fasst sie als Parameter auf, so ergeben sich Kurvenscharen.
z=x²/(2p)+y²/(2q)
Parabeln parallel zur z-y-Ebene		 z=x²/(2p)+y²/(2q)
Parabeln parallel zur z-x-Ebene		 z=x²/(2p)+y²/(2q)
Ellipsen parallel zur x-y-Ebene
Symmetrie
Die Gleichung  z=x²/(2p)+y²/(2q) ändert sich nicht, wenn man x und y durch die Gegenzahlen -x und -y ersetzt. Das heißt, dass das elliptische Paraboloid bzgl. z-y-Ebene und der z-x-Ebene symmetrisch ist.
Graph
Das elliptische Paraboloid stellt man über eine Koordinatengleichung und eine Parametergleichung wie folgt dar.

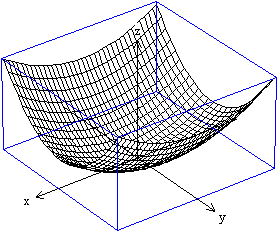
z=x²/9+y²/4 mit -3<=x<=3 und -3<=y<=3

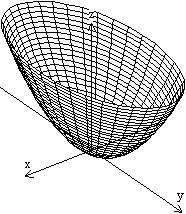
x=a*sqrt(u/h)cos(t), y=b*sqrt(u/h)sin(t), z=u 
mit a=1, b=2, h=1 und 0<=t<=2pi, 0<=u<=pi

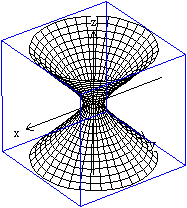
Hyperbolisches Paraboloid top
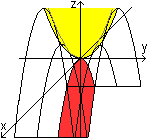...... Das hyperbolische Paraboloid hat die Gleichung z=x²/(2p)-y²/(2q), wobei p>0 und q>0 gilt.
Das Minuszeichen hat die Wirkung, dass die (rot gekennzeichnete) Parabel im Unterschied zum elliptischen Paraboloid nach unten geöffnet ist.
Es entsteht insgesamt eine "Sattelfläche". In der Zeichnung wird angedeutet, wie man sich die Entstehung vorstellen kann: Die gelb gekennzeichnete Parabel in der z-y-Ebene ist fest. Die rot gekennzeichnete Parabel wird senkrecht zur y-Achse parallel verschoben. Dabei liegen alle Scheitel auf der festen Parabel.

Kurvenscharen
Die Gleichung des hyperbolischen Paraboloids lautet z=x²/(2p)-y²/(2q). 
Hält man eine Koordinate (rot) fest und fasst sie als Parameter auf, so ergeben sich Kurvenscharen.
z=x²/(2p)-y²/(2q)
Parabeln parallel zur z-y-Ebene		 z=x²/(2p)-y²/(2q)
Parabeln parallel zur z-x-Ebene		 z=x²/(2p)-y²/(2q)
Hyperbeln parallel zur x-y-Ebene
Symmetrie
Die Gleichung  z=x²/(2p)-y²/(2q) ändert sich nicht. wenn man x und y durch die Gegenzahlen -x und -y ersetzt. Das heißt, dass die Sattelfläche bzgl. der z-y-Ebene und auch der z-x-Ebene symmetrisch ist.
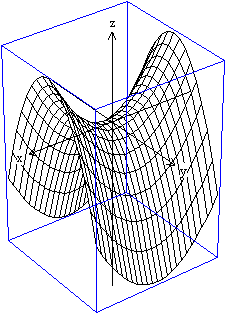
Graph 
......
 Das hyperbolische Paraboloid stellt man wie links über eine Koordinatengleichung dar.

Die Gleichung ist z=0,2x²-0,4y² mit -5<=x,y<=5.
Hyperbolisches Paraboloid als Regelfläche
Das hyperbolische Paraboloid ist eine Regelfläche. Das heißt, dass sie eine Fläche ist, die auch durch die Bewegung einer Geraden gebildet wird. 
Man kann die Gleichung z=x²/(2p)-y²/(2q) so umformen, dass man die Geradengleichungen erkennt (nach 3).
Dazu setzt man zuerst 2p=a² und 2q=b², so dass die Gleichung 2z=x²/a²-y²/b² heißt. Dann gilt 2z=(x/a+y/b)(x/a-y/b).
Man setzt u=z/(x/a-y/b) und v=2/(x/a+y/b), so dass die Gleichung z=(x/a+y/b)(x/a-y/b) durch zwei Paare von Gleichungen ersetzt werden kann.
(x/a+y/b)=2u und (x/a+y/b)=vz
(x/a-y/b)=2u und (x/a-y/b)=vz
Jede dieser Gleichungen stellt eine Ebene dar, jedes Gleichungspaar eine Gerade als Schnittgerade der Ebenen. 
Die Geradenpaare bilden das Paraboloid, wenn die Parameter u und v alle Werte durchlaufen.
Hyperbolisches Paraboloid mit rechtwinkligen Hyperbeln
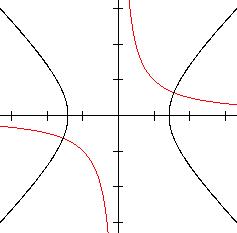...... Setzt man in der Gleichung z=x²/(2p)-y²/(2q) die Variablen p und q gleich, ergibt sich
z=(1/(2p)(x²-y²). Bei festem z wird damit eine Schar rechtwinkliger Hyperbeln beschrieben von der Art, wie sie links schwarz dargestellt ist. Hier ist p=1.

Die übliche Darstellung rechtwinkliger Hyperbeln wird in der Ebene durch die Gleichung xy=k (rot) dargestellt. Hier ist k=1.
Diese Gleichung kann erweitert werden zu kz=xy. Diese Gleichung eines Paraboloids ist einfacher und kann durch drei einfache Parametergleichungen ersetzt werden: x=u, y=t, z=(1/k)ut. 

Die Hyperbeln gehen durch eine Achteldrehung ineinander über. 
Graph mit Winplot
......
Das hyperbolische Paraboloid stellt man über die  Koordinatengleichung kz=xy (k=0.4) wie links dar.

Man erkennt die erzeugenden Geraden, die das hyperbolische Paraboloid zu einer  Regelfläche machen. 

Eine Animation u.a. findet man bei Karla Nestler, TU Dresden (URL unten).

Parabolkegel     top
Der treffende Name Parabolkegel ist nicht der übliche Name (gefunden bei 1).
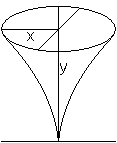...... Rotiert die Parabel z²=2px um die z-Achse, so entsteht ein Parabolkegel.

Dann ist z²=2p*sqrt(x²+y²) die Gleichung der Fläche.

Quadriert man sie, so ergibt sich eine Gleichung 4.Grades, z4=4p2(x2+y2). 
Im Unterschied zum Paraboloid ist also der Parabolkegel eine Fläche 4.Grades.

Nach (1) ist das Volumen V=(1/5)pi*x²y.

Graph mit Winplot
......
Für den Graphen gilt z=2*sqrt[sqrt(x²+y²)] mit -1<=x, y<=1.
Parabolischer Zylinder 
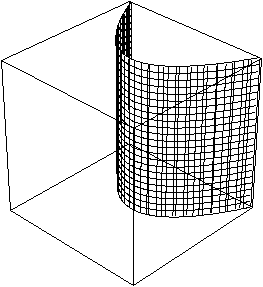...... Für den Graphen gilt x²+2y=0 mit -2,1<=x, y, z<=2,1.

Flächen zweiter Ordnung top
Das Paraboloid gehört zu den Flächen zweiter Ordnung. 
Sie ergeben sich, wenn man in einem räumlichen kartesischen Koordinatensystem die Gleichung Ax+By+Cz+Dxy+Eyz+Fzx+Gx+Hy+Kz+L=0 graphisch darstellt.
Bei bestimmten Werten für die Variablen A bis L ergeben sich im Wesentlichen die folgenden Flächen.

Kugel

Ellipsoid

Paraboloid

Hyperboloid

Zum Vergleich
Lässt man die Variable z weg, so ergibt sich die einfachere Gleichung Ax²+Bxy+Cy²+Dx+Ey+F=0. 
Im Zweidimensionalen gelangt man dann im Wesentlichen zu den den Kegelschnitten.

Kreislinie

Ellipse

Parabel

Hyperbel

Von der Parabel zum Paraboloid     top
Auf meiner Seite Parabeln findet man das Kapitel Figuren im Parabelsegment.
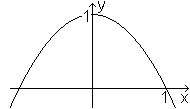...... Man erhält ein Parabelsegment wie links, wenn man die Normalparabel an der x-Achse spiegelt und um eine Einheit nach oben verschiebt. Das führt zur Funktionsgleichung f(x)=-x²+1

Es soll untersucht werden, welche Abmessungen einige Figuren im Parabelsegment mit einem  maximalen Flächeninhalt haben müssen.

Die gelben Figuren sind maximal. 

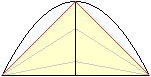
gleichsch. Dreieck
(trivial)

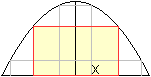
Rechteck
x=(1/3)sqrt(3)

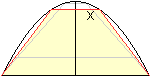
gleichschenkliges Trapez
x=1/3

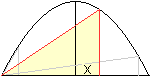
rechtw. Dreieck
x=1/3

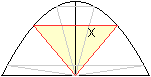
gleichsch. Dreieck
x=(1/3)sqrt(3)
Körper im Paraboloid
Es stellt sich die Frage, wie man diese Extremwertaufgaben auf das Paraboloid überträgt. 
Die gelben Körper sollen maximal sein. 

Gerader Kegel
(trivial)

Zylinder
x=(1/2)sqrt(2)

Kegelstumpf
x=1/2

unergiebig
(vielleicht doch nicht)

Kegel
x=(1/2)sqrt(2)

Paraboloid im Internet top

Deutsch

Karla Nestler (TU Dresden, Fachrichtung Mathematik)
Hyperbolisches Paraboloid

Material zur HM bei Prof. Dr. M. Stroppel (Uni-Stuttgart)
Bilder von Quadriken im Raum

Philipp Kistler  (Geschenkt)
Bauanleitung für ein hyperbolisches Paraboloid

Ralf Schaper (Fachbereich Mathematik /Informatik, Universität Kassel)
Aufgeschnittenes, elliptischen Paraboloid,  Aufgeschnittenes, hyperbolisches Paraboloid

Wikipedia 
Rotationsparaboloid, Paraboloid, Elliptisches Paraboloid,  Hyperbolisches Paraboloid,  Sattelflache, Regelfläche, 
Parabolspiegel, Parabolantenne, Zentrifugalkraft/Rotierende Flüssigkeit, Flüstergewölbe, Rotating bucket


Englisch

Eric W. Weisstein (MathWorld)
Paraboloid, Elliptic Paraboloid,  Hyperbolic Paraboloid,  Quadratic Surface

PlanetMath.org
generatrices of hyperbolic paraboloid

Richard Parris
peanut Software (Freeware-Programm WINPLOT) 

The Wolfram Demonstrations Project
Elliptic Paraboloid

Wikipedia
Paraboloid, Elliptic paraboloid,  Saddle surface,  Ruled surface, 
Parabolic reflector, Parabolic antenna,  Laminar flow

Xahlee
Paraboloid, Rotate me


Französisch

Robert FERRÉOL (mathcurve) 
PARABOLOÏDE DE RÉVOLUTION,  PARABOLOÏDE ELLIPTIQUE,  PARABOLOÏDE HYPERBOLIQUE , 
ÉLICE DU PARABOLOÏDE


Video
Youtube
Zentrifugalkraft auf rotierende Flüssigkeiten

Referenzen    top
(1) Georg Ulrich / Paul Hoffmann: Differential- und Integralrechnung zum Selbstunterricht, Hollfeld  [ISBN 3 8044 0575 4]
(2) M.J.Wygodski: Höhere Mathematik griffbereit, Braunschweig 1977 [ISBN 3 528 18309 8]
(3) W.Gellert (Hrsg.): Kleine Enzyklopädie Mathematik, Leipzig 1986 

Feedback: Emailadresse auf meiner Hauptseite

URL meiner Homepage:
http://www.mathematische-basteleien.de/

©  2011 Jürgen Köller

top
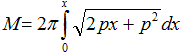
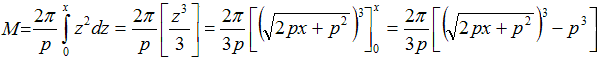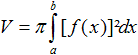
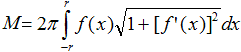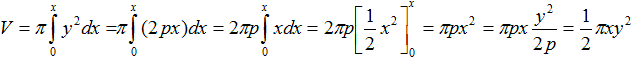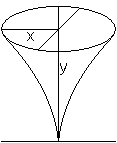
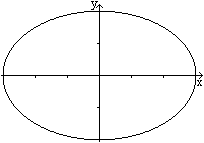
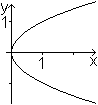
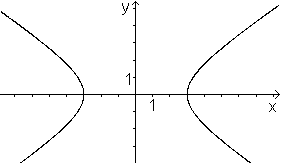