Cube Number 
Contents of this page
What is a cube number?
Cube Root 
Cube Roots of Negative Numbers?
Sequences and Series
Waring's Problem		 Special Cube Numbers
Playing with Numbers
Cube Numbers on the Internet
References
. 
To the main page    "Mathematische Basteleien"

What is a cube number?
A cube number (or a cube) is a number you can write as a product of three equal factors of natural numbers.
Formula: k=a*a*a=a³ (k and a stand for integers.)

On the other hand a cube number results by multiplying an integer by itself three times.
Formula: a*a*a=a³=k  (a and k stand for integers.)
The same factor is called the base.
After this a negative number like (-2)³= -8 or a fraction number like  (2/3)³=8/27 are suspended. 
If it is appropriate, the number 0 is also a cubic number.
These are the first 100 cube numbers. 

You can illustrate the name cube number by the following drawings. 
If a is the side of a cube, the volume is a³.

...1...

8

27
The picture pairs make a 3-D view possible. 

Cube Root   top
It is easy to find a cube number. It is more difficult, to find the base of a cube number. 
This procedure is called extracting the cube root of n. 
The cube root of a natural number can be written as  .

1 Computation with the calculator
In former times you found cube numbers by ready-reckoners, today there are calculators.
You act with the TI30 like this:
After entering the number you press the keys yx , (1/3) and finally = .
Example: [2299968] -- [yx] -- [(1/3)] --  [=] . You get 22999681/3 =132. 
It is even simpler to give in 2299968^(1/3) into the searching field of Google or Bing. 
The cube root appears after pressing the enter key. 
2 Determination by nested intervals
22999681/3
The number must be between 100 and 200 (100³=1000000 and 200³=4000000).
It must be between 130 and 140 (130³=2197000 and 140³=2744000).
It must be near 130 and 8 is on the ones place. Then 132 comes into consideration.
Result:  22999681/3=132 
3 Determination by factorization
22999681/3
You write the number in factors and develop the cube number this way.
2299968  =  8*287496  =  8*27*10648 =  8*27*8*1331=8*27*8*11*121=8*8*27*11³=(2*2*3*11)³=132. 
Result:  22999681/3 = 132.

Cube Roots of Negative Numbers?     top
There is (-2)³=-8. You could think that then (-8)1/3=-2 is. In former times this notation was common in schools, too. Today you demand that a1/3 is only defined for a>0 or a=0. The term (-8)1/3 ist not allowed. Thus you avoid conflicts as the following calculations show. 
There is (-8)1/3=(-8)2/6=[(-8)2]1/6=(64)1/6=(26 )1/6=2.
That means that (-8)1/3 would be ambiguous. You would get two results depending on the way of calculation. 

This is possible.
The equation (-2)³=-8 is changed to -(81/3)=-2. Generally x³=a leads to x=-(-a)1/3 for a<0.

Sequences and Series top
Series  of the cube numbers
There is a series to each sequence and this is the sequence of the partial sums. 
For cube numbers this is the sequence  sn= 1³+2³+3³+...+n³. 
1³+2³+3³+...+n³=[n(n+1)/2]² is given.

Proof by mathematical induction

>The statement holds for n=1:     s1=[1*(1+1)/2]²=1.
>Assume that the formula holds for all natural numbers n:   sn=[n(n+1)/2]².
>You must show that then the formula also holds for n+1:  sn+1 = [(n+1)(n+2)/2]².
Calculation:
Convert the product [(n+1)(n+2)]² into a sum at first. 
[(n+1)(n+2)]²=(n²+3n+2)²=n4+(3n+2)²+2n²(3n+2)=n4+(9n²+12n+4)+(6n³+4n²)=n4+6n³+12n²+12n+4
There is
sn+1 = sn+(n+1)³ = [n(n+1)/2]²+(n+1)³ = [n²(n+1)²+4(n+1)³]/4 = [n²(n²+2n+1)+(4n³+12n²+12n+4)]/4 
= (n4+6n³+13n²+12n+4)/4 = [(n+1)(n+2)]²/4 = [(n+1)(n+2)/2]², qed..

The formula 1³+2³+3³+...+n³=[n(n+1)/2]² contains the 
series of the natural numbers, because the sum can be written as 1+2+3+ ...+n=n(n+1)/2.

Thus there is the formula 1³+2³+3³+...+n³ = (1+2+3+...+n)²,
which is illustrated on the right.
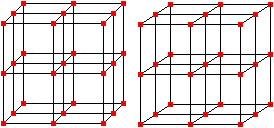
Interpretation as an arithmetic series of third order
The sequence of the cube numbers is also an arithmetic series of third order. A figure follows to explain this.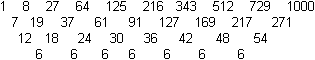
In every new row you find the difference of two numbers a row higher. 
The feature is that you reach a constant difference 6 after three steps. 
There are formulas for these sequences, so that you can prove the formula 1³+2³+3³+...+n³=[n(n+1)/2]² in another way. You can read this on Steffen Weber's (URL below) German web site. 
Series of odd numbers 
There is 1³=1, 2³=3+5, 3³=7+9+11, 4³=13+15+17+19, ...
and 1³+2³+3³+4³+... = 1+3+5+7+9+11+13+15+17+19+...
Series of the reciprocal cube numbers
There is another series of cube numbers, the one of the reciprocal cube numbers: 1/1³+1/2³+1/3³+...+1/n³.
It is convergent. You find the limit, the Riemann's zeta-function for 3, on the Wikipedia page 1729 (number). 
Series of the centered hexagonal numbers
The sequence of the centered hexagonal numbers is 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, ...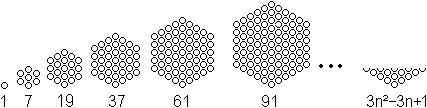
The formula is an=3n²-3n+1.
There is 1, 1+7=8, 1+7+19=27, 1+7+19+37=64, ...
The series to the sequence of the centered hexagonal numbers is the sequence of the cube numbers.
Calculation for proving: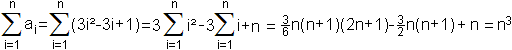

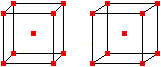
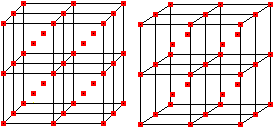
The formulas 1²+2²+3³+...+n²=(1/6)n(n+1)(2n+1) and 1+2+3+...+n=(1/2)n(n+1) are used.
Sequence of the centered cube numbers
The sequence of the centered cube numbers is 1, 9, 35, 91, 189, 341, 559, 855, 1241,...

...1...

 

9
.

35
The picture pairs make a 3-D view possible. 

The formula is an=2n³-3n²+3n-1. 
If you add two consecutive cube numbers, the centered cube numbers develop. 
This is given by 2n³-3n²+3n-1=n³+(n -1)³. 

Atomium in Brussels, a centered cube 
...... It stands 102 meters (335 ft) tall. 

There are nine steel spheres connected by tubes.

Photos from July 2011.
Sequence of the perfect numbers
T.L. Heath (1861-1940) proved that every even perfect number - except 6 - is the sum of 2(n-1)/2 cube numbers, 
for example
28=1³+3³,
496=1³+3³+5³+7³,
8128=1³+3³+5³+7³+9³+11³+13³+15³.
Source (3), page 14f.

Waring's Problem top
The English mathematician Eduard Waring (1734-1798) maintained the following statement among others.
"Every natural number is either a cube number or the sum of 2,3,4,5,6,7,8 or 9 cube numbers."
(2), page 37ff.

That means that 9 is a smallest number. 
It can be more than 9 as the following sum of 180³ with 64 (!) cubic numbers shows. 
180³ = 6³+7³+8³+...+67³+68³+69³ (1). Already 4 summands will do, 180=1³+3³+3³+5³.
The first numbers
1=1³
2=1³+1³
3=1³+1³+1³
4=1³+1³+1³+1³
5=1³+1³+1³+1³+1³ 
6=1³+1³+1³+1³+1³+1³
7=1³+1³+1³+1³+1³+1³+1³ 
15=2³+1³+1³+1³+1³+1³+1³+1³ 
23=2³+2³+1³+1³+1³+1³+1³+1³+1³ 
Dissection of the numbers <= 100, found by a simple computer program
The smallest number of the summands is determined.
>The numbers 2, 9, 16, 28, 35, 54, 65, 72, 91 have sums with 2 cubes at least: 2, 9, 16, 28, 35, 54, 65, 72, 91 
>Sums with 3 cubes: 3, 10, 17, 24, 29, 36, 43, 55, 62, 66, 73, 80, 81, 92, 99 
>Sums with 4 cubes:4, 11, 18, 25, 30, 32, 37, 44, 51, 56, 63, 67, 70, 74, 82, 88, 89, 93, 100 
>Sums with 5 cubes: 5, 12, 19, 26, 31, 33, 38, 40, 45, 52, 57, 59, 68, 71, 75, 78, 83, 90, 94, 96, 97 
>Sums with 6 cubes: 6, 13, 20, 27, 34, 39, 41, 46, 48, 53, 58, 60, 69, 76, 79, 84, 86, 95, 98 
>Sums with 7 cubes: 7, 14, 21, 42, 47, 49, 61, 77, 85, 87 
>Sums with 8 cubes: 15, 22, 50 
(All numbers are 15, 22, 50, 114, 167, 175, 186, 212, 231, 238, 303, 364, 420, 428, 454.)
>Sums with 9 cubes for 23, (and 239 only)
>8, 27, 64 are the cube numbers < 100.
There is an anecdote to the sums 1729=1³ + 12³ and 1729= 9³ + 10³, which you can read on the German Wikipedia site Tausendsiebenhundertneunundzwanzig (URL below).
Sum of cubes
The equation  x²+y²=z² leads to the Pythagorean triples (more on my German page 3-4-5-Dreieck)
The more general equation  xn+yn=zn has no solution for n>2. This is the famous Fermat's Last Theorem. Andrew Wiles und Richard Taylor proved the theorem not until 1993/95. I recommend the fascinating story in Simon Singh's bestseller Fermat's Last Theorem (5).
If you cannot write a cube number as a sum of two cubes, you can look for sums with three or more cubes. 
A nice example is  3³+4³+5³=6³, particularly, because there are four consecutive numbers.
There are more examples in the chapter Playings with Numbers below.

Special Cube Numbers top
Square numbers among the cubes 
There are cubes, which also are squares. 
You can construct them step by step by squaring cube numbers.
23 leads to 26=64, 33 to 36=729, 4³ to 46=4 096, ...
The next cube numbers and at the same time square numbers upto 1 million are 15 625, 46 656, 117 649, 262 144 und 531 441. I must not forget 1.

Palindromes among the cube numbers
343=7³
131=11³, 1030301=101³, 1003003001=1001³, ...
1367631=111³, 1030607060301=10101³, 1003006007006003001=1001001³, ...
1334996994331=11011³, 1331399339931331=110011³, ... 
1033394994933301=1011010³, ...
It is noticed that all bases are also palindromes. 
The only palindrome with a non-palindrome base is 10662526601 = 2201³ according to Martin Gardner.
Source: Patrick De Geest  (World!of numbers)

Playing with Numbers top
I show results of Lietzmann's book (1) from 1948 among other things in this chapter, extended and controlled by my computer.

A cube number is the third power of its digit sum. 
512=8³=(5+1+2)³ 
4913=17³=(4+9+1+3)³ 
5832=18³=(5+8+3+2)³ 
17576=26³=(1+7+5+7+6)³ 
19683=17³=(1+9+6+8+3)³ 
A number is the sum of the third power of its digits. 
153=1³+5³+3³
370=3³+7³+0³
371=3³+7³+1³
407=4³+0³+7³

The simple program on the right found this. 

 for x=0 to 9
for y=0 to 9
for z=0 to 9
if x*x*x+y*y*y+z*z*z=1000*x+100*y+z then print x,y,z
next z
next y
next x
Variations
22+2=2³+2³+2³

12*3=1³+2³+3³
32*5=3³+2³+5³
50*5=5³+0³+5³
51*3=5³+1³+3³

 151+3=1³+5³+1³+3³ und 153+1
370+1=3³+7³+0³+1³
371+1=3³+7³+1³+1³
400+7=4³+0³+0³+7³
401+7=4³+0³+1³+7³ und 407+1=4³+0³+1³+7³ 
464+5=4³+6³+4³+5³ und 465+4=4³+6³+4³+5³ 
624+7=6³+2³+4³+7³ und 627+4=6³+2³+4³+7³
643+7=6³+4³+3³+7³ und 647+3=6³+4³+3³+7³
733+7=7³+3³+3³+7³ und 737+3=7³+3³+3³+7³ 
773+4=7³+7³+3³+4³ und 774+3=7³+7³+3³+4³ 
914+5=9³+1³+4³+5³ und 915+4=9³+1³+4³+5³ 		 12+32=1³+2³+3³+2³ 
20+23=2³+0³+2³+3³ 
21+23=2³+1³+2³+3³ 
30+32=3³+0³+3³+2³ 
31+32=3³+1³+3³+2³ 

107*8=1³+0³+7³+8³
180*3=1³+8³+0³+3³
989*2=9³+8³+9³+2³
18*30=1³+8³+3³+0³
Terms with equal digits 
3³+7³=37*(3+7)
4³+8³=48*(4+8)
14³+7³=147*(14+7)
14³+8³=148*(14+8) 
Cube numbers are written in the digits 1 to 9. No digit is twice or more. 
125*438976=380³
8*24137569=578³
8*32461759=628³
Two numbers with common features
Example
24³=13824 and 76³=438976 
25³=15625 and 75³=421875
49³=117649 and 51³=132651
125³=1953 125 and 875³=669921875
251³=15813251 and 749³=420189749

0624³ = 242970624 and 9376³ = 824238309376
0625³ = 244140625 and 9375³ = 823974609 375

21952 = (6+8+5+9)³ and 6859 = (2+1+9+5+2)³ 

 Explanation
24+76=100, 13824 and 438976
25+75=100, 15625 and 421875
49+51=100, 117649 and 132651
125+875=1000, 1953125 and 669921875
251+749=1000, 15813251 and 420189749

0624+9376=10000, 242970624 and 824238309 376
0625+9375=10000, 244140625 and 823974609 375

21952 and 2+1+9+5+2, plus 6+8+5+9 and 6859
The bases form an arithmetic progression 
180³ = 6³+7³+8³+...+67³+68³+69³
540³ = 34³+35³+ ... +158³
2856³ = 213³+214³+ ... +555³
5544³ = 406³+407³+ ... +917³ 
16830³ = 1134³+1135³+ ... +2133³
3990³ = 290³+293³+ ... +935³
29880³ = 2108³+2111³+ ... +4292³
408³ = 149³+256³+363³
440³ = 230³+243³+265³+269³+282³
1155³ = 435³+506³+577³+648³+719³+790³
2128³ = 553³+710³+867³+1024³+1181³+1338³+1475³
168³ = 28³+41³+54³+67³+80³+93³+106³+119³
64085³ = 935³+5868³+10801³+15734³+20667³+25600³+30533³+35466³+40399³+45332³
495³ = 15³+52³+89³+126³+163³+200³+237³+274³+311³+248³

Cube Numbers on the Internet top

Deutsch

Steffen Weber (Facharbeit im Leistungskurs Mathematik)
Partialsummen und Zahlenfolgen

Wikipedia
Kubikzahl, Zentrierte Kubikzahl, Atomium, Zentrierte Sechseckszahl,  Tausendsiebenhundertneunundzwanzig


English

Eric W. Weisstein (MathWorld)
Cubic Number, Centered Cube Number, Cuban Prime,  Cubic Triangular Number

N. J. A. Sloane  (On-Line Encyclopedia of Integer Sequences) 
Integer Sequences
The cubes A000578,
Waring's problem A018888, 
Centered cube numbers  A005898
Hex (or centered hexagonal) numbers  A003215
The only integers equal to the sum of the digits of their cubes A046459
Numbers that are the sum of 2 positive cubes A003325
Numbers that are the sum of 3 positive cubes  A003072
Numbers that are the sum of 4 but no fewer positive cubes A003072
Numbers that are the sum of 5 but no fewer positive cubes A003328
Numbers that are the sum of 6 positive cubes  A003329
Smallest expression as sum of positive cubes requires exactly 7 cubes A018890
Shortest representation as sum of positive cubes requires exactly 8 cubes  A018889

Patrick De Geest (World!of Numbers)
Palindromic Cubes

Wikipedia
Cube (algebra),Centered cube number, Atomium, Centered hexagonal number,  1729 (number)

References   top
(1) Walter Lietzmann: Sonderlinge im Reich der Zahlen, Bonn 1948
(2) Rademacher-Toeplitz: Von Zahlen und Figuren, Springer, Berlin, Heidelberg, New York1968 (Nachdruck von 1930) 
(3) Maximilian Miller: Gelöste und ungelöste mathematische Probleme, Leipzig 1973 
(4) Simon Singh: Fermats letzter Satz, dtv 33052, München 2000 [ISBN 3-423-33052-X]
(5) Singh, Simon: Fermat's Last Theorem. Fourth Estate, 1997  [ISBN 1-85702-669-1]

Feedback: Email address on my main page

This page is also available in German.

URL of my Homepage:
https://www.mathematische-basteleien.de/

©  2009 Jürgen Köller

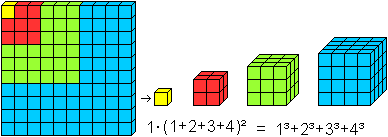
top