|
What is the Cube?
The cube is a mathematical body formed by six equal squares.
Other names are cubus or hexahedron.
In the 1980's Rubik's cube was so popular that it was simply called
"the cube".
... ...
|
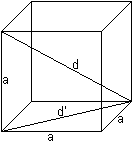
There are 12 equal edges.
Three edges meet in a corner and stand perpendicularly on each other
in pairs.
The length of an edge is a. There are
- the 12 square diagonals of the length d'=sqr(2)*a.
- the four space diagonals of the length d=sqr(3)*a.
- the volume V=a³, the surface O=6*a².
The circumscribed sphere has the radius R=a*sqr(3)/2, the inscribed
sphere the radius r=a/2. |
Views of a Cube top
Cubes in Perspective
... ... |
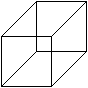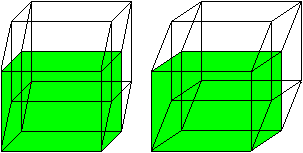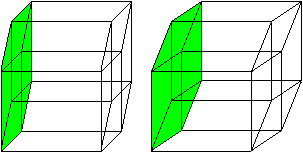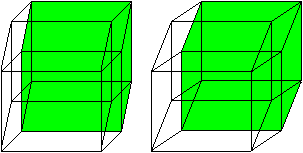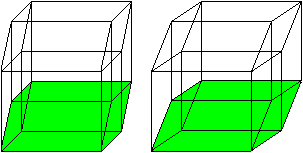
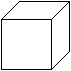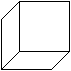
If students shall draw the picture of a cube in perspective and you
tell them before that all edges of the cube are equal some of them draw
the picture on the left.
You don't think that this is a good view of a cube. It is more a column.
Obviously the sloping lines must be shortened. |
There is the question, how much you must shorten
to get a nice view. If you have the choice
of the following four drawings most people would choose picture 3
as the best.
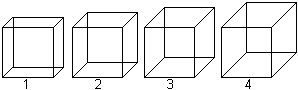The sloping line is about half as large as the true length of an egde.
Thus you get the ratio k=1/2.
The ratio depends on the angles of the sloping lines. The three following
statements produce good pictures:
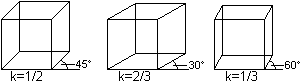
The mathematical base is the "sloping parallel projection", where all
ratios and angles are possible. You choose simple angles and simple ratios
(Book S).
There is Pohlke's theorem (also called "Main theorem of the axonometry"):
Every real 2d-tripod OABC can be produced by parallel projection of
a Cartesian 3d-tripod O'A'B'C'.
(http://www.math-inf.uni-greifswald.de/mathematik+kunst/themen.html)
More Cubes in Perspective
| ...... |
Actually the drawing with equal edges on the left was not used as a
picture of a cube. Nevertheless you may take it. The advantage is that
the length in direction of the lines are real. The "isometric perspective"
(30° instead of 45°) is not so distorted and preferred. |
Central Projection
... ... |
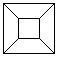Think of the edge model of a cube.
If you project it with light which comes from a point you can get the
picture on the left. |
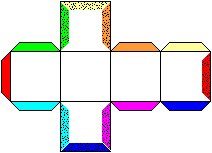
Nets of a Cube
... ... |
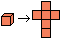Think of a paper cube and cut it along the edges. You get nets of a
cube. There are 11 nets. |
... ... |
Stereogram
You can see the cube three-dimensionally in the following picture.
More on my web page Stereogram
Shadow pictures of a rotating
cube
 |
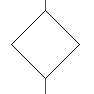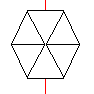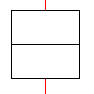For several years the "Deutsche Museum" in Munich has the department
"Das Mathematische Kabinett". A nice exhibit is a rotating edge model of
a cube. It is produced by parallel rays. You see the figures on the left
one after the other on a screen (square on the top, hexagon with diagonal
and a rectangle with a middle line).
You don't believe that these figures come from a cube and must look
twice. The cube is positioned in the way, that two edges in opposite lie
on top of each other. An axis (red) is interrupted in the middle. |
Building a Cube top
Model with squares
... ...
|
This is the well known way to build a cube.
Draw a net and give the edges stripes for gluing.
Flex the stripes and glue them on the pointed fields with the same colour.
The cube will be closed with a lid on the right. |
Model with edges
There are different methods of building cubes with rods.
>Remove the top of a match and connect the sticks with two-component
gluing.
>Take a toothpick or chopstick and connect them with balls of
modelling clay.
>Cut equal wire pieces with pincers and connect them by soldering,
so that they form a cube. It is clever to fix the three pieces of a corner
and let them touch before soldering. You can manage if you use "die
helfende Hand" (the helping hand) for two ends and the real hand for the
third end.
>Cut drinking straws in equal pieces and connect them with tripods
of florist's wire or paper clips.
More exact: There are building kits, which use 12 straws and 8 tripods
of plastic (One red tripod is removed below in the photo).
You can make tripods (below, dark green) yourself. You bend them twice
in six lines. There are bends in the tops, the two ends of a wire meet
in the middle.
... ... |
You can find a clever fashionable toy: Bar magnets form the edges,
steel balls the corners.
You pay 14€ for building kits of a cube (Springtime 2002).
In the meantime (Autumn 2003) there are different firms, which produce
them. Competition is good for the price. |
Symmetries of a Cube top
The centre of the cube is a symmetry centre.
... ...
|
The cube has nine symmetry planes.
Three planes lie parallel to the side squares and go through the centre
(picture).
Six planes go through opposite edges and two body diagonals. They divide
the cube into prisms. |
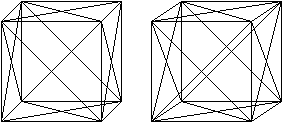
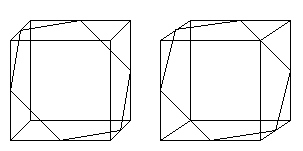
You can find 13 rotation axes. If you turn around
one of these axes, the cube goes back to itself.
The following picture illustrates these facts. The numbers under the
cubes indicate the number of turns.
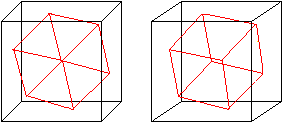
Interior Views of a Cube top
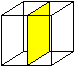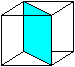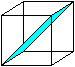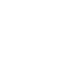
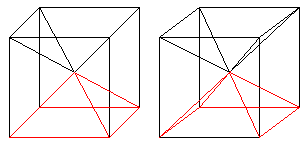
All diagonals of the surface squares
All spatial diagonals
Cube with cut corners
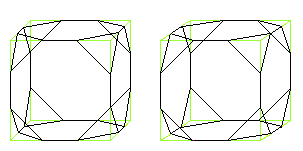
Cut the corners of a cube. Divide the edges in three equal pieces to
do this.
You get a body formed by 6 octogons and 8 equilateral triangles.
Cuboctahedron
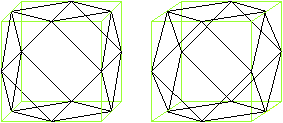
Cut the corners of a cube. Take half the edges.
You get a body formed by 6 squares and 8 equilateral triangles. .
Tetrahedron in the cube
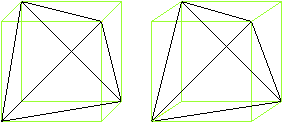
Draw some square diagonals and you get a tetrahedron.
Octahedron in the cube
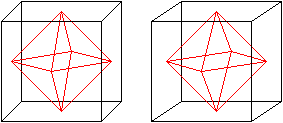
Join the centres of the squares by lines. You get an octahedron.
More: If you join the centres of the triangles of a octahedron, a cube
develops again.
Cube and octahedron are dual to each other.
Three pyramids of equal volumes
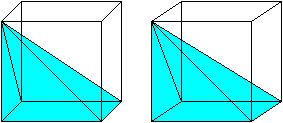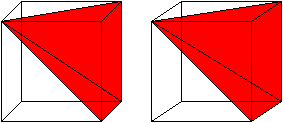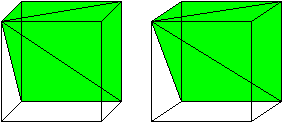
The largest square inside
a cube
The red square is the largest square which fits a cube.
The corners of the square divide the edges in 1:3 (Book G).
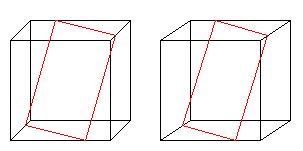
Cube in the cube
The red cube is the smallest cube which touches all sides of the black
cube (more on web page E).
Hexagon inside a cube
Join centres of some edges. You get an intersection through the cube.
The intersection line is a hexagon of the edge length sqrt(2)/2*a,
if a is the edge of the cube.
A spatial equilateral hexagon
Delos Problem (problem of cube duplication)
top
The ancient Greeks could get rid of the plague after an answer of the
oracle of Delos, if they doubled the volume of its cube altar. (This is
one version of the legend.)
... ... |
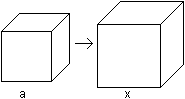The problem of the cube duplication goes to the equation 2a³=x³
and the solution x=a*2^(1/3). This was no solution to the
old Greeks, because the distance x had to be found from the length
only with circle and ruler . Now we know that this problem is unsolvable,
because only terms with square roots are possible to be constructed. Circles
and straight lines lead to linear and quadratic equations, which x³=a³
does not belong to. |
Two other problems also are unsolvable for the same reason: The conversion
of the circle into a square with the equal area ("squaring the circle")
and the division of any angle in three equal parts ("three-division of
an angle").
Polycubes top
You can form polycubes, if you add cubes touching in one or several
squares.
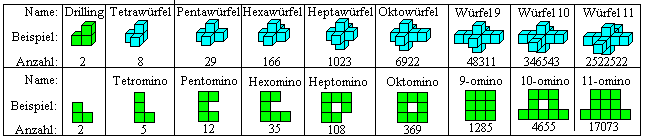
Die Zahlen geben die Anzahl der jeweiligen Würfelkörper einer
Sorte an. (Webseite K)
There are many puzzles based on polycubes. Here
is my "hit list":
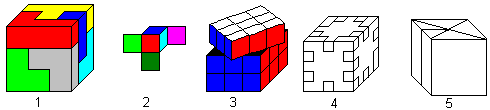
I describe the puzzles on other places of my homepage. There are 1
Soma
cube, 2 Mac Mahons Coloured Cubes, 3
Rubik's
cube, 4
Happy Cube, and 5 Origami
cube.
More cube pages are tetracubes, snake
cube, magic cube, classic
puzzle cube, (and Dice).
Hypercube (4dimensional cube) top
You find a description on my web page hypercube.
Optical Illusions top
If you like, every representation of a cube in
the plane is a optical illusions. You think you see a 3D cube, though
the drawing plane is 2D.
Well known illusions with cubes are "tilt figures".
I restrict on them.
... ... |
The Necker cube (on the left) shows a cube in two perspectives (on
the right).
You switch over from one sight to the other. A square is sometimes in
front or in the back. You can only see one view at one moment. |
... ... |
You have the questions:
Right or left? From below or above? Three or five
cubes? Five or three cubes? How many cubes?
The five pictures above are ambiguous. You see the cube from below or
above.
Do you look on a tower or into a hole?
The Cube as a Building
top
A building in the shape of a cube is not practical. Maybe because of
that architects and artists have taken the challenge and became creative.
The results are many original show-pieces and sculptures all over the world.
Here is a small look back on the unforgettable Expo 2000 in Hanover,
Germany.
1 The T-Digit of the "Deutsche Telekom" was a centre of the exhibition
area. You could look at a large screen sitting on the steps of show stairs
where (even in the sunshine) an impressive light TV picture was to be seen.
Have a look at the French Open in Paris.
2 The exhibition cube of Mexico was seen from nearly every point
of the area.
3 The Iceland cube was unforgettable: It was dark blue and over
it there was a water layer. Inside there was a round water pond whose surface
was used as a screen for a movie about Iceland in the bird's-eye view.
In the end of the performance an artificial geyser erupted.
4 I forgot to take a photo of the Norwegian cube building equipped
with a waterfall :-(.
... ... |
Therefore I restrict on a model, which you could find on the internet
before the Expo opening. (The waterfall didn't become so mighty.)
You entered the "room of silence" after a slight shower. You could sit
on the hard floor for some minutes and watch the Norwegian sceneries on
all six squares. From time to time stones rolled down the rocks (only acoustically).
It was not allowed to talk. My wife... (censorship!) |
The
Cube on the Internet top
German
H. B. Meyer (Polyeder aus Flechtstreifen)
Hexaeder,
Würfel (spezial)
Richard Mischak
Würfelspiele
Wikipedia
Würfel
(Geometrie), Platonischer
Körper, Delisches
Problem, Expo
2000
English
David Eppstein (Geometry Junkyard)
Box
in a Box
Eric Weisstein (MathWorld)
Cube,
Prince Rupert's
Cube
H. B. Meyer (Polyeder aus Flechtstreifen)
Cube,
Cube (special)
Henry Bottomley
Circumnavigating
a cube and a tetrahedron
Jim Loy
Regular
Solids
Wikipedia
Cube,
Platonic solid,
Doubling the cube,
Expo 2000
References top
(G) Martin Gardner: Mathematischer Karneval, Ullstein Berlin 1977 (Seite
61)
(S) Hans Simon, Kurt Stahl: Mathematik, Formeln und Gesetze, Leipzig
1979 (Seite 471ff.)
(K) Michael Keller (früher: http://members.aol.com/wgreview/polyenum.html)
(E) David Eppstein (http://www.ics.uci.edu/~eppstein/junkyard/box-in-box.html)
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
http://www.mathematische-basteleien.de/
©
2002 Jürgen Köller
top |
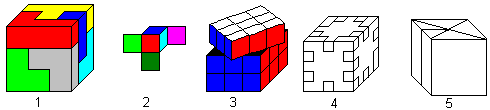