Was sind MacMahons Farbwürfel?
MacMahons Würfel sind die Würfel, die entstehen,
wenn man sechs verschiedene Farben in allen möglichen Kombinationen
auf die sechs Seitenflächen verteilt.
... ... |
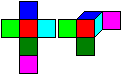Die Farben sind nicht vorgeschrieben. Sie können
zum Beispiel rot (1), hellblau (2) dunkelblau (3), dunkelgrün (4),
hellgrün (5) und pink (6) sein.
Links wird ein möglicher Würfel dargestellt,
als Netz und als Schrägbild mit drei umgeklappten Quadratseiten. |
P.A.MacMahon war ein englischer Mathematiker und Major.
Er lebte von 1854 bis 1929.
Es gibt 30
MacMahon-Würfel
top
... ... |
Gibt man die Zahlen 1, 2, 3, 4, 5 und 6 vor und bildet
alle Umstellungen (Permutationen) der sechs Zahlen, so kommt man auf 1*2*3*4*5*6=6!=720
Würfel. Jetzt sind aber auch die Würfel aufgeführt, die
sich durch Drehungen um eine der 13 Achsen ineinander überführen
lassen. Es gibt 24 Drehungen dieser Art. Also gibt es nur 720:24 =30 verschiedene
Würfel. |
Das folgende Bild illustriert diesen Sachverhalt. Die Zahlen
unter den Würfeln geben die Anzahl der Drehungen an.
Bau der Farbwürfel
top
Die 30 Würfel kann man auch durch systematisches
Färben gewinnen:
.... .. |
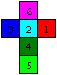
>Alle Würfel erhalten hinten die Farbe pink.
>In jeder Zeile erhält die Vorderfläche eine
der sechs Farben.
>In jeder Zeile bekommt die Fläche unten die dritte
passende Farbe.
>Die restlichen drei Flächen erhalten in einer Zeile
alle Permutationen der übrigen drei Farben.
Die Bezeichnungen wie Ab stammen von Conway (s.u.) |
Will man sich mit den Farbwürfeln beschäftigen,
so muss man sie unbedingt bauen.
... ... |
Man kann z.B. 30 runde Haftetiketten mit jeweils 1 bis
6 (an Stelle der Farben) beschriften und auf Spielwürfel kleben. Damit
man die Übersicht behält, sollte jeder Würfel einen Namen
wie Ab bekommen.
Es ist natürlich schöner, wenn man größere
Würfel verwendet und sie mit den sechs Farben versieht. |
Würfelkörper top
Bei den Puzzles mit den Farbwürfeln
geht es in erster Linie darum, aus ihnen Quader oder Würfel mit einfarbigen
Seitenflächen zu bauen.
Die folgenden vier Körper
sind relativ leicht zu finden.
Der Würfel links wird zweimal
um eine 1x2x2-Scheibe nach links hin erweitert. Es enstehen 3x2x2 und 4x2x2-Quader.
Für die Ecken des großen
Würfels rechts wird der kleine Würfel links verwendet. Die 19
nicht angegebenen Würfel findet man leicht.
... ... |
Der L-förmige Körper links wird aus symmetrischen
Farbwürfeln aufgebaut.
Das Besondere ist, dass innen als zusätzliche Bedingung
gleiche Farben aufeinanderstoßen. Das ist die sogenannte Domino-Bedingung
(Gardner). |
Das MacMahon Problem
top
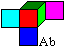
Das zentrale Puzzle ist das MacMahon-Problem.
... ...
|
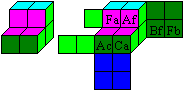
Man wählt aus den 30 Würfeln einen Würfel,
z.B. den Würfel Ab. |
 ... |
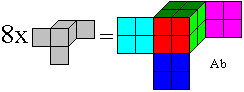Es bleiben 29 Würfel übrig. Aus ihnen wählt
man acht, um einen 2x2x2 Würfel zu bauen mit den gleichen Farben auf
den entsprechenden Seitenflächen wie der Würfel Ab. Erschwerend
kommt hinzu, dass innen gleiche Farben aufeinanderliegen müssen. |
Die Lösung findet man nicht durch Probieren. Man muss
systematisch vorgehen.
Es folgt eine Beschreibung des Lösungsweges für
den Würfel Ab.
Zunächst werden die vier Würfel unten gesucht.
Lege dazu alle Würfel so hin, dass dunkelblau unten ist.
Für den Würfel unten, links, vorne kommen
Bc, Ca, Df, Ed und Fe in Frage. Da bei Df, Ed, Fe innen und außen
gleiche Farben lägen, scheiden Sie aus. Es bleiben Bc und Ca
übrig. (Bc wird hier nicht weiter verfolgt. Man käme zu einer
zweiten Lösung.)
Für den Würfel unten, rechts, vorne kommenBd,
Cf, Da, Ec und Fe in Frage. Bd bleibt übrig.
Für den Würfel unten, links, hinten kommenBf
und Ce in Frage. Bf bleibt übrig.
Für den Würfel unten, rechts, hinten kommt
nur Ea in Frage.
Drehe jetzt für die obere Schicht alle Würfel,
so dass dunkelgrün oben liegt.
Für den Würfel oben, links, vorne kommen
Be und Cd in Frage. Be bleibt übrig.
Für den Würfel oben, rechts, vorne kommt
nur Fa in Frage.
Für den Würfel oben, links, hinten kommt
nur Da in Frage.
Für den Würfel oben, rechts, hinten kommt
nur Bc in Frage.
Die Lösung ist also:
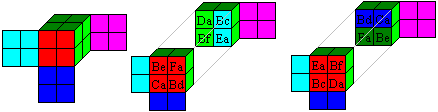Rechts wird noch die zweite Lösung dargestellt, die
bei der Suche des ersten Würfels schon erwähnt wurde. Es werden
die gleichen Würfel verwendet. Sie liegen zum Würfelmittelpunkt
symmetrisch und sind verdreht.
J.H.Conway kommt das Verdienst einer umfassenden Lösung
des Problems zu.
...... ... |
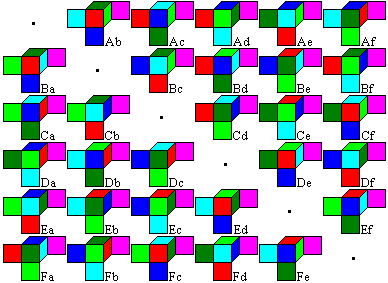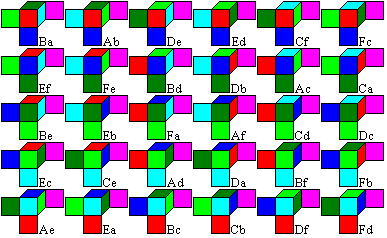
Er ordnete die 30 Würfel in einem 6x6-Feld an, wobei
er die Hauptdiagonale frei hielt.
Die Spalten werden a,b,c,d,e,f genannt, die Zeilen A,B,C,D,E,F.
So erhält jeder Würfel je nach seiner Lage ein
Paar aus einem großen und einem kleinen Buchstaben als Name. |
Das Besondere an der Tabelle ist, dass sie für alle
Würfel alle Lösungen des MacMahon-Problems enthält.
Will man z.B.den Farbwürfel Ab vergrößert
als 2x2x2-Würfel bauen, kann man die acht Würfel leicht auswählen:
Man geht in der Tabelle von Würfel Ab aus zum Spiegelwürfel
Ba und wählt die übrigen acht Würfel in der Zeile und der
Spalte, in der der Würfel Ba liegt.
... ... |
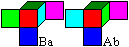In dieser Anordnung liegen zueinander spiegelbildliche
Farbwürfel spiegelbildlich zur Hauptdiagonalen. So sind z.B. die Würfel
Ab und Ba Spiegelbilder. |
Noch eine Besonderheit:
... .... |
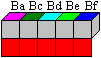Legt man die fünf Würfeln einer Zeile oder
Spalte zu einer 1x1x5-Stange und achtet darauf, dass irgendeine Farbe
unten liegt, so liegen die restlichen fünf Farben oben. |
Das Mayblox-Problem
top
Beim Mayblox-Problem werden wieder acht Würfel vorgegeben,
aus denen ein 2x2x2-Würfel zu bauen ist. Jetzt steht aber ein kleiner
Würfel als Vorlage nicht zur Verfügung. Darin liegt eine zusätzliche
Schwierigkeit.
Das Kowalewski -
Problem top
... ... |
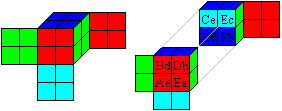Der deutsche Mathematiker G. Kowalewski änderte
das 8-Würfel-Problem ab:
Er verlangte rechts und links bzw. vorne und hinten gleiche
Farben, oben eine dritte und unten eine vierte Farbe. Innen sollten gleiche
Farben zusammentreffen.
Dieses Problem hat zwei Lösungen. Eine Lösung
wird rechts dargestellt. Für die zweite Lösung benötigt
man 8 weitere Würfel. |
Instant Insanity top
Im Jahre 1967 brachte die Firma Parker Brothers die "color
matching box" unter dem Namen "Instant Insanity" auf den Markt. Es hieß
in Deutschland "Vier verrückt" oder "Katzenjammer-Puzzle". Es wurde
12 Millionen mal verkauft (!?).
... ... |
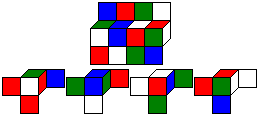Dieses Puzzle besteht aus vier farbigen Würfeln.
Im Unterschied zu den MacMahon-Würfeln werden aber nur vier verschiedene
Farben verwendet.
Aufgabe des Puzzles ist es, die Würfel so zu einer
1x1x4-Stange zusammenzustellen, dass auf allen vier Seitenflächen
die vier Farben erscheinen.
Es gibt im Wesentlichen nur eine Lösung. |
... ... |
Es ist auch möglich, eine Stange aus MacMahon-Würfeln
zu bauen, so dass auf allen vier Seitenflächen sechs verschiedene
Farben erscheinen und darüber hinaus innen Farbanschlüsse gewährleistet
sind. Bei dieser auch optisch schönen Lösung sind sogar die Enden
der Stange gleichfarbig. |
... ... |
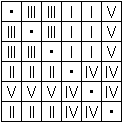Man kann die 30 Würfel in 5 Gruppen zu je 6 Würfeln
aufteilen, so dass jedesmal eine Stange gebaut werden kann wie eben beschrieben.
[Lösung von Zoltan Perjés, Buch 6].
Sie werden links im Conway-Schema mit den römischen
Ziffern I bis VI gekennzeichnet. Die gezeichnete Stange trägt die
Ziffer I.
Das Besondere ist, dass die Würfel einer Stange
zusammenliegen und dass man die Würfel einer Stange zum Teil nicht
nur nebeneinander, sondern auch voreinander oder untereinander anordnen
kann, ohne dass sich die Eigenschaften der sechs unterschiedlichen
Farben und des Farbanschlusses ändern (Beobachtung von Torsten Sillke). |
Farbwürfel
im Internet
top
Deutsch
Wikipedia
Percy
Alexander MacMahon
Englisch
Jaap Scherpius (Jaap's Puzzle
Page)
Octacube,
Instant
Insanity
John J. O'Connor & Edmund F.
Robertson, University of St Andrews
Percy
Alexander MacMahon
Kadon Enterprises Inc.
Frank
Armbruster invented Instant Insanity
Torsten Sillke
MacMahon's
cubes (Multiple Cubes, Probabilities,
References)
Wikipedia
Percy
MacMahon, Instant
Insanity, MacMahon
Squares
Französisch
Charles-É. Jean
(Dictionnaire de mathématiques récréatives)
Cube
coloré
Referenzen top
(1) Gerhard Kowalewski: Alte und neue mathematische Spiele,
Leipzig 1930 (Reprint bei Teubner, Stuttgart 1978)
(2) Bruno Kerst: Mathematische Spiele, Berlin 1933 (Nachdruck:
Martin Sändig, Wiesbaden 1968)
(3) Gardner, Martin: Mathematische Knobeleien, Braunschweig
1980 (Vieweg)
(4) Rüdiger Thiele: Das große Spielvergnügen,
Leipzig 1984 (Urania-Verlag)
(5) Gardner, Martin: Mathematische Hexereien, Berlin
1988 (Ullstein)
(6) Gardner, Martin: Fractal Music, Hypercards
and More Math. Recreations from SA Magazin, New York 1991 (Freeman)
(7) Rüdiger Thiele, Konrad Haase: Der verzauberte
Raum, Leipzig/Jena/Berlin 1991 (Urania-Verlag)
(8) Rüdiger Thiele, Konrad Haase: Teufelsspiele,
Leipzig/Jena/Berlin 1991 (Urania-Verlag)
Ich bedanke mich bei Sabine Sprankel für die
Anregung zu dieser Seite und bei Torsten Sillke für Unterstützung.
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2002 Jürgen Köller
top |