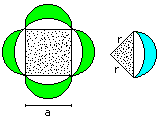|
What are Arc-Sided Figures?
Arc-sided figures are figures, which are formed by (circular)
arcs.
This section contains a collection of arc figures arranged
by the number of corners. On this web page a corner is the point, where
two arcs touch.
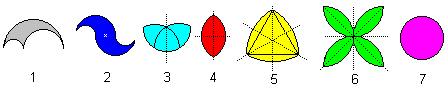 The colours of the figures mark the symmetry.
The colours of the figures mark the symmetry.
1 No symmetry
2 symmetry with 1 centre
3 symmetry with 1 axis |
4 symmetry with 2 axes
5 symmetry with 3 axes |
6 symmetry with 4 axes
7 symmetry with 5 axes and more |
The letters below the following figures
mean: A = area, U = circumference.
A student wrote to me
to say that he had recalculated all the figures. I could rest assured.
They are correct.
Figures of two
circles top
Lense
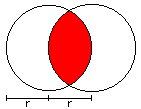
A = [2/3*Pi - 1/2*sqrt(3)]*r²
U = 4/3*Pi*r
|
Lense
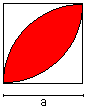
A = [1/2*Pi - 1]*a²
U = Pi*a
|
Mushroom
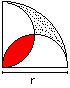
A = (1/8*Pi - 1/4]*r²
U = 1/2*Pi*r
|
Three-quarter Moon

A = [1/2*Pi + 1]*r²
U = 2*Pi*r
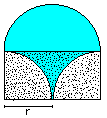
Figures of three
circles top
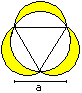
Tricorn
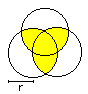
A = [Pi - 1/2*sqrt(3)]*r²
U=2*Pi*r
|
Bug's Eyes
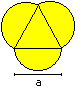
A = [1/4*sqrt(3) + 3/8*Pi]*a²
U = 3/2*Pi*a
|
Three circles
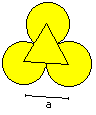
A = [1/4*sqrt(3) + 5/8*Pi]*a²
U = 5/2*Pi*a
|
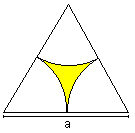
Figures of four
circles top
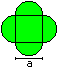
Diamonds
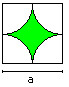
A = (1 - Pi/4)*a²
U = Pi*a
|
Axe head
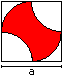
A = 1/2*a²
U = Pi*a
|
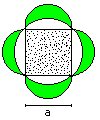
Arc square

A = [1 + 1/3*Pi - sqrt(3)]*a²
U = 2/3*Pi*a
|
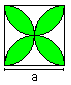
Four-Leaf Clover
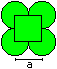
A = [1 + 3/4*Pi]*a²
U = 3*Pi*a
|
Dumb-Bell
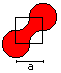
A = [1 + 1/4*Pi]*a²
U = 2*Pi*a
|
Heart
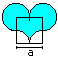
A = [1 + 1/4*Pi]*a²
U = 2*Pi*a
|
Hook

A = 3/4*Pi*r²
U = 3*Pi*r
|
Salinon
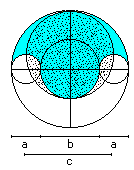
A = 1/4*PI*(a+b)² = 1/4*Pi*c²
U = Pi*(2*a+b)
|
Worm
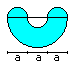
A = 5/4*Pi*a²
U = 3*Pi*a
|
Ring
A = [1/24*Pi + 1/4*sqrt(3)]*a²
U = [2/3*sqrt(3)+3/2]*Pi*a
|
Hour-glass
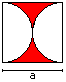
A = [1 - 1/4*Pi]*a²
U = Pi*a
|
Chicken egg
A = [3*Pi - sqrt(2)*Pi - 1)]*r²
U = [3-1/2*sqrt(2)]*Pi*r
|
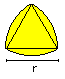
Figures of five
circles top
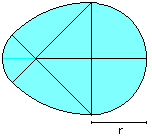
Crescent Moons (Hippokrates)
A = a²
U = [sqrt(2)*+2]*a
|
Tulip

A=Pi*r²
U = (2*Pi+2)*r
|
Figures of six
circles top
Rosette
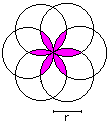
A = [2*Pi - 3*sqrt(3)]*r²
U = 4*Pi*r
|
Rosette
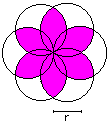
A = 2*Pi *r²
U = 4*Pi*r
|
Bear head
A = [1/4*sqrt(3) + 1/16*Pi]*a²
U = Pi*a
|
Curve with constant width
A = 1/2*Pi*a² + Pi*ab + Pi*b² - 1/2*sqr(3)*a²
U = Pi*(a+2b)
|
Humming-Top

A = 2*a²
U = 2*Pi*a
|
Figures of eight
circles top
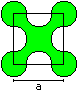
Cross
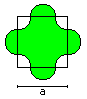
A = [1 + 1/16*Pi]*a²
U = 3/2*Pi*a
|
Cross
A = [1 + 1/16*Pi]*a²
U = 5/2*Pi*a
|
Rings top
Circumscribed and inscribed circle of
an equilateral triangle
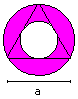
A = 1/4*Pi*a²
U = sqr(3)*Pi*a (more precise: boundary line)
|
Circumscribed and inscribed circle of
a square
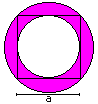
A = 1/4*Pi*a²
U = [1+sqrt(2)]*Pi*a (more precise: boundary line)
|
How
to Calculate Arc-Sided Figures top
You calculate arc-sided figures by searching basic figures,
which form the figures and the areas of which you know. You must multiply,
subtract, add them.
This method will be explained by
three figures.
1st Example
The only basic figure is the semi-circle, that appears
four times. The area is generally 1/2*Pi*r². You replace the radius
r by a/2 and/or 3a/2.
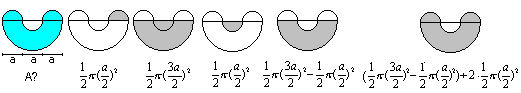 The best way is to only write the term on the right and simplify
it. The result is A=5/4*Pi*a².
The best way is to only write the term on the right and simplify
it. The result is A=5/4*Pi*a².
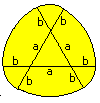
2nd Example
The second figure consists of an equilateral triangle
and three congruent arcs.
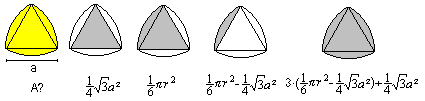
The result is A = [1/2*Pi - 1/2*sqr(3)]*r².
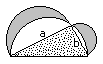
3rd Example
The third figure is formed by two congruent arcs. The
basic figures are a quarter circle and a half square.
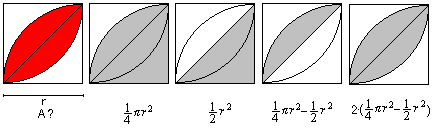
The result is A = [1/2*Pi - 1]*r².
...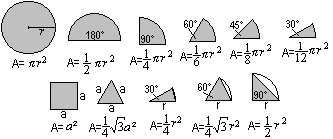 . . |
A collection of important basic figures |
Some solutions top
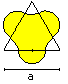
Area of the arc square
... |
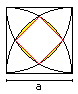 |
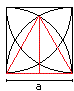
The calculation has two parts:
1 You calculate the area of the inner red square.
2 You calculate the area of the yellow segments. |
1
... ... ... |
 ... ... |
There is a equilateral triangle inside the square with
the height h=(1/2)sqrt(3)a.
The blue lines are the diagonals of the square. One half
diagonal has the length h-(1/2)a=(1/2)[sqrt(3)-1]a
Thus the area of the square is A1 = 4*(1/2){(1/2)[sqrt(3)-1]a}²
= (1/2)[4-2sqrt(3)]a²=[2-sqrt(3)]a². |
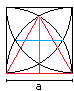
2
...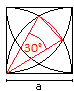 ... ... |
There is a 30° sector inside the square.
The area of the segment is the difference between the
area of the sector and the area of the isosceles triangle with the sides
a. There are four segments.
A2 = 4*[(1/12)pi*a²-(1/4)a²] = [(1/3)pi-1]a² |
Result
A=A1 + A2 = [2-sqrt(3)]a²
+ [(1/3)pi-1]a² = [1-sqrt(3)+(1/3)pi]a²
Area
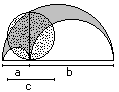
of the Orbital
 |
 |
I use the formulas of the lense AL =
[1/2*Pi - 1]*a² and
the arc square AB = [1 + 1/3*Pi - sqrt(3)]*a². |
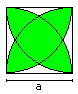 |
The area of the orbital is A = 2*AL - AB.
That means A=2*[1/2*Pi - 1]*a² -[1 + 1/3*Pi - sqrt(3)]*a²
oder A = Pi*a²-2a²-a²-(1/3)Pi*a²+sqrt(3)a² oder
A = (2/3)Pi*a²-3a²+sqrt(3)a² oder A =
[sqrt(3) + 2/3*Pi - 3]*a², qed. |
Squaring the Circle
top
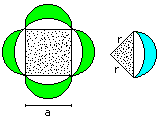 |
In the history of mathematics Hippokrates' crescent moons
were important, because you can draw a triangle (or four-sided figures
in other cases) with ruler and compass having the same area. Mathematicians
guessed you were able to find a square with the same area as a circle in
a similar way. But since the 19th century it is known that this is not
possible, because Pi is a transcendental number (Ferdinand Lindemann 1882). |
The crescent moon figures
are still interesting today, because five "constructable" arc figures with
two corners are known. It is unknown, whether there are more.
You find more about circles on my German pages Kreis,
Kreise
im Kreis, Arbelos,
Halbkreis,
Zweikreisfiguren,
and Gleichdick.
Arc-Sided
Figures on the Internet top
German
Barbara Flütsch (Mathe-Aufgaben)
Kreis
und Kreisteile: Berechnungen
S MART
Aufgabenbereich
"Kreisteile - auch Segmente"
Wikipedia
Kreis
(Geometrie), Reuleaux-Dreieck,
Arbelos
English
David Eppstein (The Geometry Junkyard)
Circles
and Spheres
Eric W. Weisstein (MathWorld)
Piecewise
Circular Curve, Circle,
Arc,
Triangle
Arcs, Semicircle,
Arbelos,
Lens,
Yin-Yang,
Salinon,
Reuleaux
Triangle
Tim Lexen
Bending
the Law of Sines, Making
Tricurves
University of Cambridge (nrich mathematics)
Arclets
(Shapes made from arcs)
Wikipedia
Circle,
Reuleaux
triangle,
Arbelos,
Salinon,
Semicircle,
Ring
(geometric)
References top
Walter Lietzmann: Altes und Neues vom Kreis, Leipzig
und Berlin 1935
Eugen Beutel: Die Quadratur des Kreises, Leipzig und
Berlin 1942
Maximilian Miller: Gelöste und ungelöste mathematische
Probleme, Leipzig 1973
10a in 1986/87, thank you
Gail from Oregon Coast, thank you for supporting me in
my translation.
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
2001 Jürgen Köller
top |
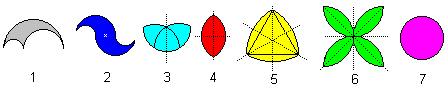

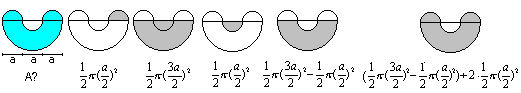
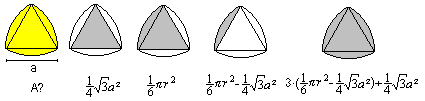
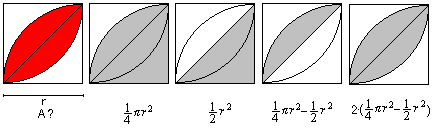





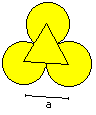
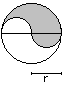






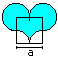


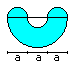













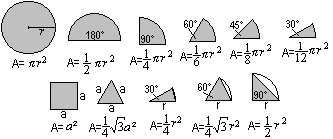 .
.
 ...
... ...
... ...
...