|
Was ist das regelmäßiges
Zwölfeck?

|
Das regelmäßige Zwölfeck ist ein Vieleck
mit
12 gleich langen Seiten,
12 gleich großen Innenwinkeln. |
Das Zwölfeck heißt auch Dodekagon.
Im Englischen ist der Name Dodecagon üblich. Man
findet auch
12 sided figure.
Auf dieser Seite wird das
regelmäßige
Zwölfeck meist einfach Zwölfeck genannt.
Größen
des Zwölfecks
top
Winkel im Zwölfeck
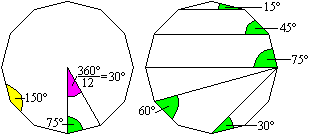
Formeln
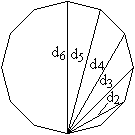
Fünf Diagonalen
|

Radius des Umkreises, Radius des Inkreises, Höhe
|
Ist die Seite a gegeben, so lassen sich daraus
der Radius r des Inkreises, der Radius
R des Umkreises, die
Diagonalen d2
,d3
,
d4
,
d5
und d6, die Höhe
h,der Flächeninhalt
A
und der Umfang
U
errechnen.
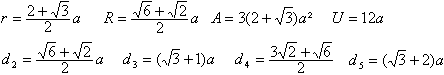 Es gilt weiter d6=2R und h=2r. Ferner ist d2=R.
Es gilt weiter d6=2R und h=2r. Ferner ist d2=R.
Zur Herleitung der Formeln
Auf meiner Seite Regelmäßiges
Vieleck werden die folgenden Formeln besprochen.
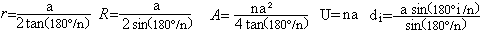
Setzt man n=12, so ergeben sich
die oben stehenden Formeln.
Unter anderem werden die weniger
bekannten Beziehungen sin15°=[sqrt(6)-sqrt(2)]/4 und cos15°=[sqrt(6)+sqrt(2)]/4
verwendet.
Eine
einfache Flächenformel
...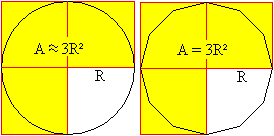 ... ... |
Die Fläche eines Kreises kann man bei einem Fehler
von 4,5% mit der Fläche von drei Quadraten veranschaulichen. Die Quadrate
haben den Umkreisradius als Seitenlänge.
Für das Zwölfeck gilt die Beziehung exakt. |
Zum Nachweis berechnet man 3R² und gelangt zu A.
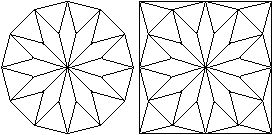
Kürschak's Tile
|
Das ist ein eleganterer Weg um A=3R² einzusehen. |
Konstruktion
eines Zwölfecks
top
Man zeichnet zuerst ein Sechseck.
...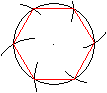 ... ... |
Man zeichnet einen Kreis und trägt auf dem Kreisbogen
sechsmal den gleichen Radius ab.
Die Verbindungslinien der Schnittpunkte bilden ein Sechseck. |
...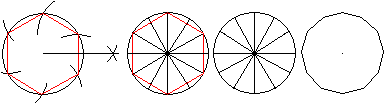 ... ... |
Dann zeichnet man vom Mittelpunkt aus die Senkrechten
zu den Sechseckseiten.
Links wird eine der sechs Senkrechten konstruiert. |
Man erhält die Eckpunkte des Zwölfecks.
Diagonalen top
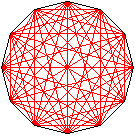
|
Das regelmäßige Vieleck hat n(n-3)/2 Diagonalen.
Dann hat das Zwölfeck 54 Diagonalen. |

>6 Diagonalen verbinden gegenüberliegende Eckpunkte.
>12 Diagonalen verbinden jeden zweiten, 12 jeden dritten,
12 jeden vierten und 12 jeden fünften Eckpunkt.
>Die Diagonalen bilden vier voneinander unabhängige
Sterne, die Dodekagramme.
>Der Stern 1 besteht aus zwei regelmäßigen
Sechsecken, die mit der Drehung eines Sechsecks um 30° zur Deckung
gebracht werden können.
>Der Stern 2 besteht aus drei Quadraten, die mit Drehungen
eines Quadrats um jeweils 30° zur Deckung gebracht werden können.
>Der Stern 3 besteht aus vier gleichseitigen Dreiecken,
die mit Drehungen eines Dreiecks um jeweils 30° zur Deckung gebracht
werden können.
>Der Stern 4 kann in einem Zug gezeichnet werden.
>Die Winkel an den Spitzen der Sterne sind 120°, 60°,
90° und 30°.
Parkettierung
und Zwölfeck
top
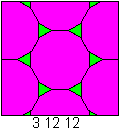
Man kann die Ebene mit Zwölfecken
überdecken.
Gleichseitige Dreiecke, Quadrate
und regelmäßige Sechsecke füllen die Lücken.
...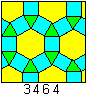 ... ...
|
Bei der Parkettierung der Ebene mit Dreiecken, Quadraten
und Sechsecken entstehen Zwölfecke. |
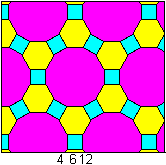
Man kann die letzte Zeichnung
auch anders deuten.
...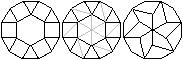 ... ...
|
Greift man ein Zwölfeck heraus und zeichnet Diagonalen
in das Quadrat und Sechseck ein, kann man 12 Vierecke aus einem halben
Quadrat und gleichseitigen Dreieck erkennen. |
Diese kongruenten Vierecke bilden einen Stern und parkettieren
das Zwölfeck.
Parkettierung eines Zwölfecks
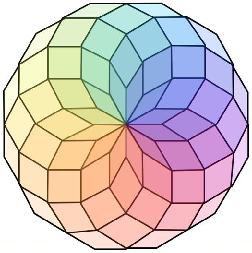 © Corinna
Beuermann-Kulp
© Corinna
Beuermann-Kulp
Unregelmäßige
Zwölfecke top
 .. ..
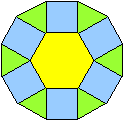
GriechischesKreuz
|
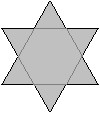
Hexagramm
|
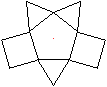
333445
|
Ein zwölfeckiger
Turm top
... ... ...
|
Ein berühmter Turm ist der Torre del Oro
in Sevilla (Spanien).
Er hat als Grundriss ein regelmäßiges Zwölfeck.
Ein besseres Urlaubsphoto habe ich nicht gefunden.
Damals - 1998 - fand ich die Fluchtlinien im Parkett
interessanter als den Turm. |
Zwölfeck im
Internet top
Deutsch
Hans Walser
Zerlegungen
des Zwölfeckes (.pdf-Datei)
Werner Brefeld
Regelmäßiges
Vieleck und Zerschneiden
Wikipedia
Zwölfeck,
Torre
del Oro
Englisch
Alexander Bogomolny (cut-the-knot)
Kürschak's
Tile and Theorem
Eric W. Weisstein (MathWorld)
Dodecagon,
Dodecagram
John Page
Dodecagon
Michael S. Schneider
Chartres
Rose Window Geometry
Wikipedia
Dodecagon,
Torre
del Oro
Referenzen top
H.Martyn Cundy, A.P.Rollet: Mathematical Models, Oxford
1961, Seite 25f.
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2005 Jürgen Köller
top |

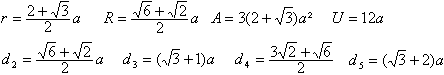




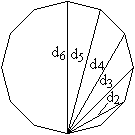

 ...
...
 ...
... ...
...
 ...
... ...
... ..
..


 ...
...