What are the Dice?
 |
The dice have 21 points. The numbers 1 to 6 appear on the six sides
of a cube. -
You throw the dice by hand or by a leather dice cup. You turn the cup
upside down and you let the dice roll to a standstill. It is by chance
which number appears on top. This is the attraction of throwing the dice. |
The dice are used in many board games. They often determine the playing.
They give the game unexpected turns and add excitement to the games.
There are 30 Dice top
... ... |
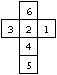If you give the numbers 1, 2, 3, 4, 5, and 6 and form all permutations
of the six numbers, you get 1*2*3*4*5*6=6!=720 cubes. Now there are also
those dice among them, which are the same, because you can get them by
turning around 13 axes. There are 24 turnings.
Hence you only have 720:24 =30 different cubes. |
The following drawing illustrates this. (The numbers
under the cubes give you the number of turnings.)
Appearance of
the Standard Die top
 ... |
The die has six sides for six numbers. If you try all possible ways
to spread them out, you get 30 dice. - Every die has its reflection. You
can find the possibilities if you reverse the numbers beside the 1.
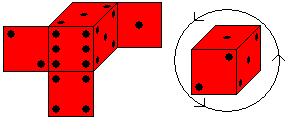
You can mark every die by a number with six digits: Start with 1, go
upwards, go around 1 counter clockwise and add the number that appears
opposite the number 1 on the die. - The red die has 123546 for instance.
The dice on the left are ordered by these numbers. |
You find more about the number 30 at my Website Macmahons
Coloured Cubes.
There is only the red die in the western world.
 ... |
This die has two characteristics:
>The sides opposite each other always add to 7.
>If you look at the corner with the numbers 1, 2, and 3 they are arranged
counter clockwise. |
Most of the dice makers follow these rules.
 ... |
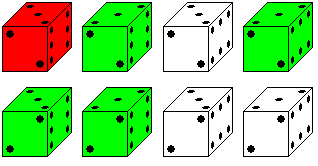There is a way the dice can be different.
There are two ways of placing the points of number 2, 3, or 6,
which change into themselves by turning through 180°. This leads to
eight pictures.
The red die is the most frequent. But I also found the green ones. |
Four puzzles with dice will follow now.
Guessing the Sum top
. .. |
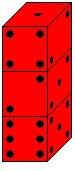Build a tower of several dice.
Is it possible to find the sum of the points of the hidden horizontal
cube sides?
In this case the tower is formed by three dice. Five surfaces would
be counted: The under side of the top die, and the top and bottom sides
of the two lower dice.
Solution: You take 1 at the top and count the number of the lower cubes.
Number 6 is opposite the 1 side. You add 7 for each die. The sum is 6+2x7=20. |
Cube Puzzle top
 ... |
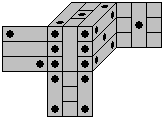You can make a nice cube puzzle, if you cut the die in nine bars.
The vertical bars are in the middle layer, the horizontal ones on the outside.
Then the puzzle is more interesting. |
... ... |
You can also form a 3x3x3-cube with 9 V-Triominos (drawing) or with
Soma cubes. Draw points on them. |
Rubik's Dice top
Rubik's dice is a black plastic dice 7cm x 7cm x 7cm with circular holes
instead of points. There are seven white squared tiles with red circles,
which you can lay inside the cube. The tiles directly lying at the holes
stick to walls inside. You can remove them with two connected sticks. The
tiles close the holes in red or in white. You have found a solution, when
all points have become white.
You will soon notice, that you can`t solve the puzzle by trying. There
are too many possibilities with seven tiles for closing the holes. Moving
the tiles is difficult, too.
Act like this: You can look inside the cube and can recognize the patterns
of both sides of the tiles. Draw them. The tiles show a number with two
digits on the top right (meaning?), which can be used as names. There is
the following image:
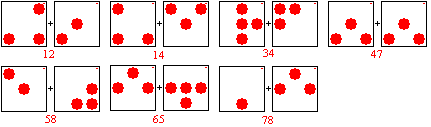
Now the solution is simple. If you like, don't read further and solve
the puzzle yourself...
Solution:
Tile 78 (left side) only fits on the six, then tile 65 (left side)
only fits on the five, then tile 34 (left side) only fits on the four,
then tile 58 (right side) only fits on the three, then tile 12 (right side)
only fits on the two, and then tile 14 (left side) only fits on the one.
Tile 47 is useless.
There is only one solution.
In the meantime I opened the cube with a saw :-(
to
scan one side of a tile. Besides I was curious to see how the tiles stick
inside. The tiles are made of iron. They are held by six ring magnets.
They are inside the cube in the centres. You can see their contours from
outside.
Sum Problemtop
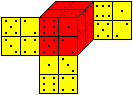Give eight dice. Build a 2x2x2 cube, so that the sum of the points
on each side is the same.
Here is one of 20 736 solutions with the sum 14.
You find more at the German magazine <bild der Wissenschaft> 3-1980.
More Dice Shapes top
The cube belongs to the five Platonic solids. These are solids, which
are only formed by regular polygons. They are called tetrahedron,
hexahedron (cube), octahedron, dodecahedron, and icosahedron.
You can build dice after their model.
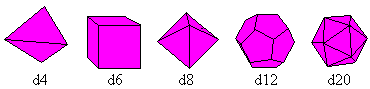
You can find 4,6, 8,12 or 20 numbers by throwing the dice. The number
at the top counts. The tetrahedron is an exception. The hidden number counts
or the one, that is on top as seen in the scan.
I found more interesting solids, which are possible to play the dice
from the mathematical view. They are convex, are formed by congruent
polygons and have the same position related to the centre of gravity.
("Properties of Dice", URL below).
There are more dice forms. I chose two of them.
 ... |
The die d10 is interesting. It has the shape of a double pyramid with
a pentagon as the mutual base. It shows the numbers 0 to 9, the digits
of the decimal system. So you can find random numbers with several digits
by several dice of this kind. |
. .. |
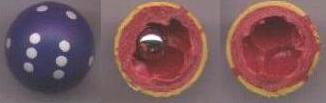The die in ball form is funny:
There is an iron ball inside the die, which only rest in one of the
six hollows.
So the points lie at the top. |
 ... |
There are many possibilities to find random numbers. You can lay six
balls marked with number 1 to 6 in a box similar to the national lottery.
You can mix them and then take one without looking at. The chosen number
is the random number. If you play the "dice" a second time, you must put
back the ball in the box first.
This is the normal model for a die in mathematics to classify the die
in a theory. |
In spite of the inflation of dice forms:
The normal d6 is and will stay the standard die.
It has several advantages:
>The number 6 is not too small and not too large. You can play well
with six random numbers.
>The normal die rolls best, especially if the corners are rounded.
It is common.
>You can make them easily, because the cube sides are perpendicular
to each other.
Marked Dice top
You call dice, which show some numbers more frequently than others,
marked dice.
You can manipulate the normal die in different ways.
> The dice don`t show all six different numbers, some are missing. You
always see three sides of the dice from one direction. Therefore three
numbers can be missing.
> You can slightly change the shape of the dice. You can irregularly
round off the corners, the areas of a side can be different.
> You can manipulate the dice inside. If there is a metal piece inside
the dice, but not symmetrically, the dice will stop rolling, so the heavy
piece will lay at the bottom. - A hollow space will be at the top.
> You can prepare the surface of a cube side, so it will stop on this
side.
> You can use magnetic power, even switched on by radio control.
The Computer Plays the
Dice top
You can simulate the dice with the computer.
There is a random generator in all programming languages (i.e. Visual Basic),
which produce random numbers between 0 and 1 (A=RND).
 ... |
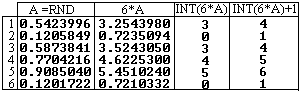You multiply these numbers by 6, cut off the decimals with the function
INT and add 1.
This is shown with six examples on the left.
You get the random numbers 4, 1, 4, 5 ,6, and 1. |
It is easy to throw the dice 6000x this way.
 ... |
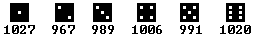The frequency table shows that the numbers from 1 to 6 appear nearly
equally, about 1000x. |
This also predicts the probability theory. The probability finding a number
(i.e. three) is 1/6 (=1000/6000). This result is better and better, if
the number of throwing the dice is bigger. On the other hand a good random
generator must not distribute the numbers too regularly. This is the difficulty
with programming a good random generator.
A probability statement like 1/6 is of no use
for a single throwing. You don`t know which number will appear next. Each
throwing is independent from the one before.
Dice on the Internet top
English
ARJAN VERWEIJ
Dice
Kevin Cook
Collection of Dice
Edd Peg Jr (mathpuzzle.com)
Fair
Dice
Eric W. Weisstein (MathWorld)
Dice
Jacqueline de Swart
Jacqueline 's dicecollection,
Linkpage
Klaus Æ. Mogensen
Properties of Dice
Leo van der Heijdt
Welcome to the Homepage
of DICE Collector (Dutch / English)
Steve Wunter
A
Brief History of Dice
Wikipedia
Dice
German
Antje Hofmann
Online-Spiel
: Mensch - ärgere - dich - nicht
Faroul
Würfel
Wikipedia
Spielwürfel
References (German) top
(1) Robert E.Lembke, Michael Schiff: Das große Haus- und Familienbuch
der Spiele, Frankfurt a. M. 1970
(2) Martin Gardner: Mathematische Hexereien, Berlin 1988
(3) Rüdiger Thiele, Konrad Haase: Der verzauberte Raum, Leipzig
1991
(4) Reiner Knizia: Das große Buch der Würfelspiele (124
Spiele), München 2000
Gail from Oregon Coast, thank you for supporting me in my translation.
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
http://www.mathematische-basteleien.de/
©
2001 Jürgen Köller
top |
