|
Großes Rhombenikosidodekaeder
|
Was ist das große Rhombenikosidodekaeder?
... ...
|
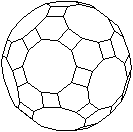
Das große Rhombenikosidodekaeder
ist ein Körper, der von 30 Quadraten, 20 regelmäßigen Sechsecken
und 12 regelmäßigen Zehnecken gebildet wird.
Der Körper heißt auch nach
einer möglichen Entstehung "abgestumpftes Ikosidodekaeder". |
Neben den 30+20+12=62 Seitenflächen
hat das große Rhombenikosidodekaeder 180 Kanten
und 120 Eckpunkte.
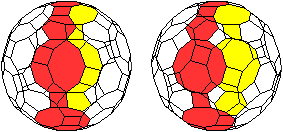
Die beiden folgenden, nebeneinander
liegenden Bilder ermöglichen mit dem "Stereoblick" eine dreidimensionale
Ansicht des Körpers.
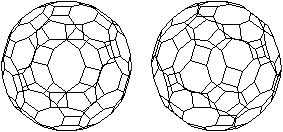
durchsichtig
|
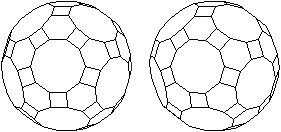
undurchsichtig
|
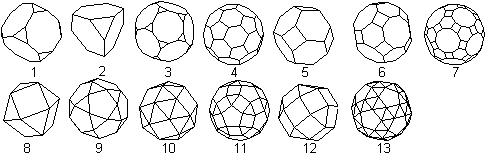Da beim großen Rhombenikosidodekaeder
(7) an jeder Ecke regelmäßige Vielecke in gleicher Weise aufeinandertreffen,
gehört es zu den 13
archimedischen
Körpern.
Abgestumpftes
Ikosidodekaeder? top
... ... |
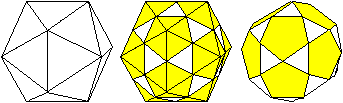Verbindet man die Kantenmitten eines Ikosaeders und entfernt
die dann entstehenden Pyramiden an den Ecken, so entsteht ein Ikosidodekaeder. |
... ... |
Man kann vom Ikosidodekaeder wiederum Eckpyramiden entfernen.
Dann werden aus den Fünfecken Zehnecke, aus den Dreiecken Sechsecke
und die entfernte Pyramide hinterlässt scheinbar ein Quadrat.
Es sieht so aus, als ob man das große Rhombenikosidodekaeder
aus einem Ikosidodekaeder gewinnen könne. |
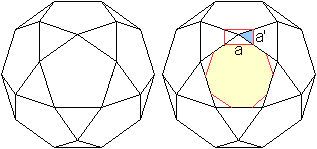
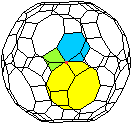
Betrachtet man dieses Vorgehen genauer, so ergibt sich ein
Widerspruch.
Wenn das Fünfeck zu einem regelmäßigen
Zehneck mit der Seite a werden soll, muss man die Ecken abschneiden.
Das blaue Dreieck kann aber nicht auch die Grundseite
a haben. Da es gleichseitig ist, müssten die vier Seitenlängen
der Pyramide auch gleich a sein. Das ist nicht möglich.
Die Grundfläche der Pyramide kann also kein Quadrat
werden, sondern sie ist ein Rechteck mit den Seiten a und a'.
Der Name abgestumpftes Ikosidodekaeder
ist also missverständlich.
... ....
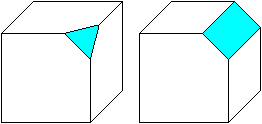abgestumpft und abgeschrägt..
|
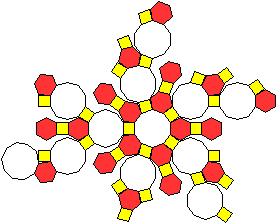
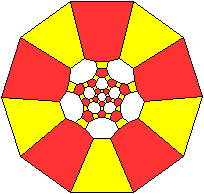
Auf der Seite von Geneviève Tulloue (URL unten)
wird demonstriert, dass man das große Rhombenikosidodekaeder
als abgeschrägtes Pentagondodekaeder ansehen kann. |
... .. |
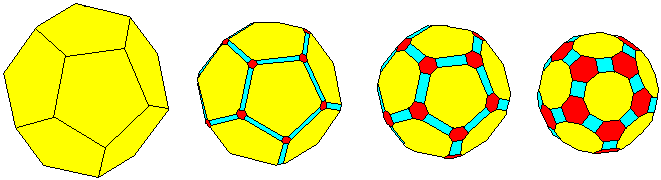Auf der Webseite wird das in einem Applet dargestellt.
Das Pentagondodekaeder wird so weit abgeschrägt,
dass aus den Fünfecken regelmäßige Zehnecke und dazwischen
Quadrate und regelmäßige Sechsecke entstehen. |
Beschreibungen top
Umgebung der Vielecke
|
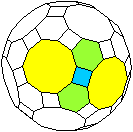
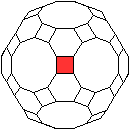
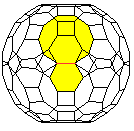
Jedes Quadrat ist von zwei Sechsecken und zwei Zehnecken
umgeben. |
|
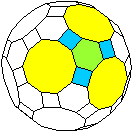
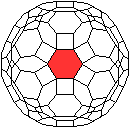
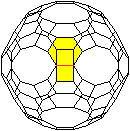
Jedes Sechseck ist von drei Quadraten und drei Zehnecken
umgeben. |
|
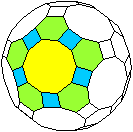
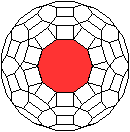
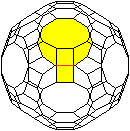
Jedes Zehneck ist von fünf Quadraten und fünf
Sechsecken umgeben. |
Parallele
Seitenflächen
|
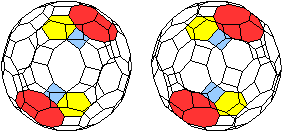
Gleiche Vielecke liegen paarweise parallel zueinander. |
Halbierung
Umläuft man längs einer Halbierungslinie den
Körper, so folgen Zehneck/Quadrat/Zehneck und Sechseck/Quadrat/Sechseck
abwechselnd aufeinander.
Parallelprojektionen
Das Quadrat, das Sechseck, das Zehneck,
die Kanten 4/10, 4/6 und 4/10 und der Eckpunkt liegen vorne.
Ein
Netz und ein Schlegel-Diagramm
Diagonalen
660 Flächendiagonalen
... .... |
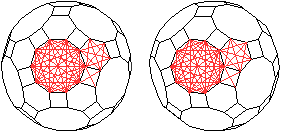Die Diagonalen der Zehnecke, der Sechsecke und der Quadrate
sind die Flächendiagonalen des Rhombenikosidodekaeder.
Das Zehneck hat 35, das Sechseck 9 und das Quadrat hat
2 Diagonalen.
Das führt zu insgesamt 12*35+20*9+30*2=660 Flächendiagonalen. |
6300
Raumdiagonalen
... ... |
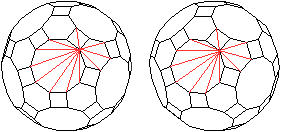Von jedem der 120 Eckpunkte gehen Verbindungslinien zu
den anderen Eckpunkten aus. Das sind 11 Flächendiagonalen und 3 Kanten,
wie die Zeichnung zeigt. In 120-14=106 Punkten enden dann Raumdiagonalen.
Das führt zu insgesamt (1/2)*120*105=6300 Raumdiagonalen des Rhombenikosidodekaeder. |
Bilanz
Auf meiner Seite Dreieckszahlensteht:
"Verbindet man n Punkte mit allen möglichen geraden Linien, so ergeben
sich 1+2+3+...+(n-1)=(1/2)(n-1)n Strecken."
Für das große Rhombenikosidodekaeder
bedeutet das, dass es (1/2)*120*119=7140 Verbindungslinien gibt. Das sind
die 180 Kanten, 660 Flächendiagonalen und 6300 Raumdiagonalen.
Größen top
Das große Rhombenikosidodekaeder
sei durch die Kantenlänge a gegeben.
Daraus lassen sich weitere Größen wie Radius
R
der Umkugel, Radius
rk der Kantenkugel, Volumen V,
Oberfläche O , Abstand der Quadrate
d4, Abstand
der Sechsecke d6 und Abstand der Zehnecke
d10
berechnen.
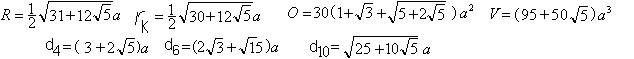
Herleitung
der Formeln
Folgende Formeln werden u.a. in diesem Kapitel benutzt.
Im regelmäßigen Fünfeck
mit der Seitenlänge a ist die Diagonale d=(1/2)[sqrt(5)+1]a.
Im Pentagondodekaeder
ist der Radius der Inkugel r=(1/20)sqrt[250+110sqrt(5)]a.
Radius
der Umkugel
... ... |
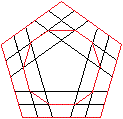Oben wird dargestellt, dass man das große Rhombenikosidodekaeder
aus dem Pentagondodekaeder gewinnen kann, indem man die Kanten abschrägt.
Genauer muss man die Seiten eines
Fünfecks des Dodekaeders in fünf gleiche Teile teilen und durch
die Teilpunkte zu den Seiten Parallelen zeichnen. Verbindet man bestimmte
Schnittpunkte wie links, entsteht das Zehneck des großen Rhombenikosidodekaeders. |
... ... |
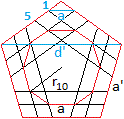Man beschriftet die Zeichnung und liest folgende Formeln
ab.
Es ergibt sich nach dem 2.Strahlensatz a:d'=1:5 oder
a=(1/5)d'.
Für die Diagonale des Fünfecks gilt d'=(1/2)[sqrt(5)+1]a'.
Dann ist a=(1/5)d'=(1/5)(1/2)[sqrt(5)+1]a' oder a=(1/10)[sqrt(5)+1]a'.
Daraus ergibt sich a'=10a/[sqrt(5)+1] oder a'=(10/4)[sqrt(5)-1]a
oder a'=(5/2)[sqrt(5)-1]a. |
... ... |
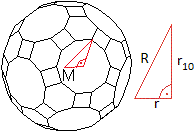M sei der Mittelpunkt des Körpers.
Man kann im Körper ein rechtwinkliges Dreieck ausmachen,
in dem R als Hypotenuse erscheint.
r=(1/20)sqrt[250+110sqrt(5)]a' ist der Radius der Inkugel
des Pentagondodekaeders.
r10 = (1/2)[sqrt(5)+1]a
ist der Radius des Umkreises des Zehnecks.
Es gilt R²=r²+r10²
oder R²=(1/400)[250+110sqrt(5)]a'²+(1/4)[sqrt(5)+1]²a²
oder
Setzt man a'=(5/2)[sqrt(5)-1]a ein und vereinfacht, so
erhält man R²=(1/4)[31+12sqrt(5)]a².
Dann ist R=(1/2)sqrt[31+12sqrt(5)]a, wzbw |
Kantenkugel
Bei archimedischen Körpern liegen die Kantenmitten
auf einer Kugel, der Kantenkugel.
 |
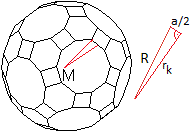Der Radius rk der Kantenkugel kann über
den Radius R der Umkugel bestimmt werden.
Im rechtwinkligen Dreieck gilt rk² =
R²-[(1/2)a]² = (1/4)[31+12sqrt(5)]a²-(1/4)a² = (1/4)[30+12sqrt(5)]a².
Dann ist rk= (1/2)sqrt[30+12sqrt(5)]a, wzbw. |
Oberfläche
O
O = 30*A4+20*A6+12*A10
O = 30*a² + 20*(3/2)sqrt(3)a² +12*(5/2)sqrt[5+2sqrt(5)]a²
O = 30a²+30sqrt(3)a²+30sqrt[5+2sqrt(5)]a²
O = 30*{1+sqrt(3)+sqrt[5+2sqrt(5)]}a²,
wzbw.
Abstand
der Quadrate
d4
... ... |
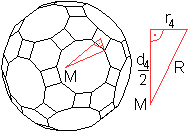M sei der Mittelpunkt des Körpers.
Man kann im Körper ein rechtwinkliges Dreieck ausmachen,
in dem d4/2 als Kathete erscheint.
Es gilt (d4/2)² = R²-r4²
und weiter
(d4/2)² = R²-r4²
= {(1/2)sqrt[31+12sqrt(5)]a}²-[(1/2)sqrt(2)a]² =...
= [29/4+3sqrt(5)]a².
Weiter ist d4/2 = (1/2)sqrt[29+12sqrt(5)]a
oder dank Derive d4/2 = (1/2)[3+2sqrt(5)]a.
Dann ist d4 = [3+2sqrt(5)]a,
wzbw. |
Abstand
der Sechsecke
d6
... ... |
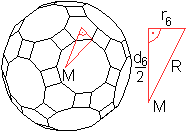M sei der Mittelpunkt des Körpers.
Man kann im Körper ein rechtwinkliges Dreieck ausmachen,
in dem d4/2 als Kathete erscheint.
Es gilt (d6/2)² = R²-r6²
und weiter
(d6/2)² = R²-R6²
= {(1/2)sqrt[31+12sqrt(5)]a}²-a² = [27/4+3sqrt(5)]a².
Weiter ist d6/2 = (1/2)sqrt[27+12sqrt(5)]a
oder dank Derive d6/2 = (1/2)[2sqrt(3)+sqrt(15)]a.
Dann ist d6 = [2sqrt(3)+sqrt(15)]a,
wzbw. |
Abstand
der Zehnecke d10
... ... |
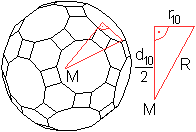M sei der Mittelpunkt des Körpers.
Man kann im Körper ein rechtwinkliges Dreieck ausmachen,
in dem d10/2 als Kathete erscheint.
Es gilt (d10/2)² = R²-r10²
und weiter (d10/2)² = R²-R10²
= {(1/2)sqrt[31+12sqrt(5)]a}²-{(1/2)[sqrt(5)+1]a}²
= [25/4+(5/2)sqrt(5)]a².
Weiter ist d10/2 = (1/2)sqrt[25+10sqrt(5)]a.
Schließlich ist d10 = sqrt[25+10sqrt(5)]a,
wzbw. |
Volumen
V
Verbindet man den Mittelpunkt des großen Rhombenikosidodekaeders
mit seinen Eckpunkten, so erhält man eine Aufteilung des Körpers
in drei verschiedene Pyramiden. Das Volumen ergibt sich aus der Summe der
Einzelpyramiden.
V = 30*(1/3)A4(d4/2) +
20*(1/3)A6(d6/2)
+
12*(1/3)A10(d10/2)
V = 30*(1/3)a²(1/2)[3+2sqrt(5)]a
...+20*(1/3)[(3/2)sqrt(3)a²](1/2)[2sqrt(3)+sqrt(15)]a
...+12*(1/3){(5/2)sqrt[5+2sqrt(5)]a²}(1/2)sqrt[25+10sqrt(5)]a
V = ...
V = 5[3+2sqrt(5)]a³+5[6+3sqrt(5)]a³+5[5sqrt5)+10]a³
V =...
V = [95+50sqrt(5)]a³, wzbw.
Dualer Körper top
Hexakisikosaeder
... ... |
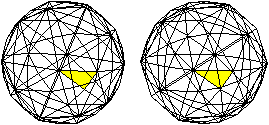Verbindet man die Mittelpunkte benachbarter Seitenflächen
des großen Rhombenikosidodekaeders,
so entsteht der duale Körper, das Hexakisikosaeder oder das Disdyakistriakontaeder. |
Rhombenikosidodekaeder
im Internet top
Deutsch
Wikipedia
Ikosidodekaederstumpf,
Archimedischer
Körper, Catalanischer
Körper, Hexakisikosaeder
Englisch
Eric.W.Weisstein (MathWorld)
Great
Rhombicosidodecahedron, Dual: Disdyakis
Triacontahedron
Geneviève Tulloue ( Figures Animées pour
la Physique )
Polyhedra
(Applets)
G. Korthals Altes
Paper
Model Truncated Icosidodecahedron
Poly
A program
for downloading (Poly is a shareware program for exploring and constructing
polyhedra)
Die meisten Zeichnungen auf dieser Seite entstanden
mit Hilfe dieses Programms.
Wikipedia
Truncated
icosidodecahedron,
Archimedean
solid, Catalan
solid, Disdyakis
triacontahedron
Referenzen top
(1) H.Martyn Cundy and A.P.Rollett: Mathematical Models,
Oxford 1961 (Seite 113)
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2008, erweitert 2/2014, Jürgen Köller
top |
