What is a Hexomino?
 Rectangles
around Hexominos
top
 Rectangle Problem top  The problem is the same with hexominos. All 35 hexominos together have 35*6=210 squares. So there are many possible rectangles. Example: Can you form a rectangle 21 x 10? Statement: You cannot solve this rectangle problem.
On the other side you can colour the single hexominos.  You can see that there are two ways to colour the hexominos. There are odd and even hexominos. In both cases you get an even number of coloured squares: 24*3, 11*4 or 11*2. There is a contradiction: 105 is odd, the number of the coloured cubes is even. Result: A rectangle 21*10 is impossible. You can prove in the same way, too, that there are
no rectangles such as 14*15 or 6*35.
By the way you cannot build a rectangle with figures of 7 or more squares for another reason:
Figures of Hexominos top
 Figures of the Same Hexominos top  There are many figures without rules (blue). It is nice
you take the symmetry into account.
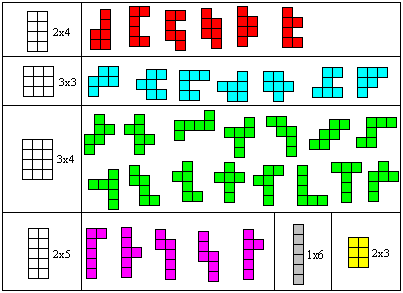
Special Hexominos top Symmetric Hexominos 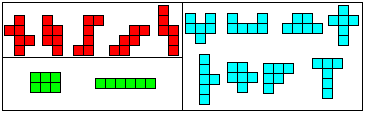 Nets of a Cube top 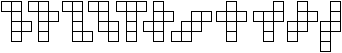 11 Hexominos can be used as nets of a cube.
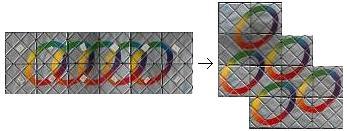 Rubik's Magic is a folding game with the main problem: Transform a mat of 6x2 squares into a heart-shaped figure. Then five linked rings change into five free rings on the reverse side. If you fold the basic figure on the two symmetry axes, you get the simple rectangles 1x6 and 2x3. There are more complicated folding sequences, which lead to 16 hexominos. They are coloured in red below. It is remarkable that only odd pentominos develop. 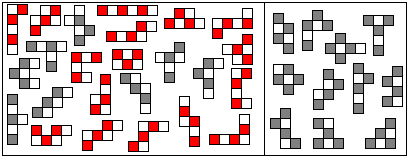
Hexacubes top
Hexominos on the Internet top Deutsch Andrew Clarkes Poly Seiten
Richard Mischak (Zahlenjagd)
English Andrew Clarke's THE POLY PAGES
gamepuzzles
Gerard's Home Page
Joseph Myers
Steven Dutch
Torsten Sillke
Wikipedia
References
top
This page is also available in German. URL of
my Homepage:
© 2002 Jürgen Köller |
 ...
...