|
Was ist ein Halbzylinder?
...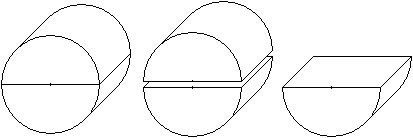 ... ...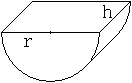 ... ... |
Teilt man einen Zylinder durch
eine Ebene, die seine Achse enthält, so entstehen zwei kongruente
Halbzylinder.
Wie beim Zylinder bestimmen der Radius und die Höhe
den Halbzylinder. |
Größen
des Halbzylinders top
Sind bei einem Halbzylinder der Radius r und die
Höhe h gegeben, lassen sich das Volumen V, der Mantel
M
und die Oberfläche O berechnen.
... ... ... |
Für den Zylinder gilt V=pi*r²h, M=2pi*rh und
O=2pi*rh+2pi*r².
Für den Halbzylinder gilt dann V=(1/2)pi*r²h,
M=(2+pi)rh
und O=pi*r²+(2+pi)rh. |
Die Summe der Kanten ist
k=4r+2h+pi*r+pi*r oder k=(4+2pi)r+2h.
Besondere Ansichten
top
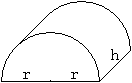
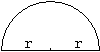
von vorne
|
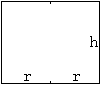
von oben
|
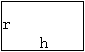
von der Seite
|
|
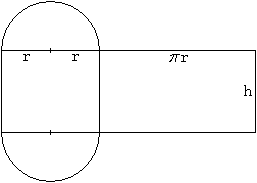
ausgebreitet
|
Schwerpunkt
des Halbzylinders top
...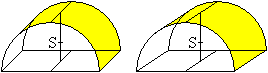 ... ... |
Der Schwerpunkt des Halbzylinders liegt über der
Mitte der Grundfläche im Abstand a=(4r)/(3pi) oder angenähert
a=0,42r.
Das Bildpaar ermöglicht eine dreidimensionale Sicht. |
Herleitung
Auf meiner Webseite Schwerpunkt
von Figuren wird die Formel für die Lage des Schwerpunktes
im Halbkreis wie folgt hergeleitet.
...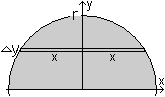 ... ... |
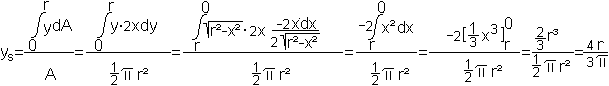
"dx statt dy" heißt, die Grenzen in sqrt(r²-0²)=r
und sqrt(r²-r²)=0 zu ändern. |
Ergebnis: Die erste Koordinate
ist aus Gründen der Symmetrie xs=0.
Die zweite Koordinate ist ys=(4r)/(3pi) oder
angenähert ys=0,42r.
Man kann einen Halbkreis
als den Ausartungsfall eines Halbzylinder sehen mit h=0.
Deshalb kann man das Ergebnis xs=0 und ys=(4r)/(3pi)
übernehmen.
Aus Gründen der Symmetrie liegt der Schwerpunkt
in Richtung der Höhe bei (1/2)h.
Eine Extremwertaufgabe
top
Für den Zylinder gibt es die Konservendosen-Aufgabe:
Welche Form muss ein Zylinder haben, damit sein Volumen
bei gegebener Oberfläche maximal ist?
Für den Halbzylinder heißt die entsprechende
Aufgabe:
Welche Form muss ein Halbzylinder haben, damit sein Volumen
bei gegebener Oberfläche maximal ist?
Lösung
...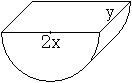 ... ... |
Der Radius sei für diese Aufgabe x und die Höhe
y.
Die Nebenbedingung ist O=2xy+pi*x²+pi*xy oder y=(O-pi*x²)/(2x+pi*x).
Es gilt V=(1/2)pi*x²y. Die Zielfunktion ist V(x)=(1/2)pi*x²(O-pi*x²)/(2x+pi*x). |
Vereinfacht ist V(x)=(1/2)pi*x²[O/(2x+pi*x)-pi*x/(4+2pi)]=[pi*O/(4+2pi)]x-[pi²/(4+2pi)]x³.
Dann ist V'(x)=[(pi*O)/(4+2pi)]-(3pi²)/(4+2pi)]x².
Für einen möglichen Maximalwert gilt V'(x)=0
oder [(pi*O)/(4+2pi)]-[(3pi²)/(4+2pi)]x²=0.
Dann ist x²=O/(3pi) oder x1=sqrt[O/(3pi)]
/\ x2=-sqrt[O/(3pi)].
Für die positive Lösung gilt V''(x)=-6[pi²/(4+4pi)]x1<0.
Damit ist die Maximalstelle gesichert.
Für x1=x=sqrt[O/(3pi)] ist
...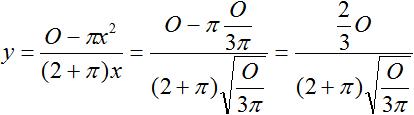
Die Form wird durch das Verhältnis (2x)/y bestimmt.
...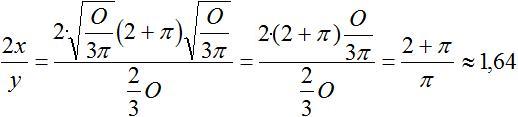
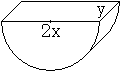
Ergebnis
Bei einem Zylinder maximalen Volumens ist die Form durch
(2r)/h=1 bestimmt, beim Halbzylinder durch (2r)/h=(2+pi)/pi.
Es gibt eine abgewandelte
Aufgabe. Man vertauscht dazu die Oberfläche und das Volumen.
Welche Form muss ein Halbzylinder haben, damit seine
Oberfläche bei gegebenem Volumen maximal ist? Auch hier hat der maximale
Körper wie bei der abgewandelten Konservendosen-Aufgabe die gleiche
Form wie bei der Ausgangsaufgabe.
Körper
mit Halbzylindern top
Ein Körper aus Halbzylinder
und Quader
...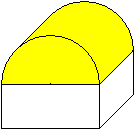 ... ... |
Es gibt Zelte oder Gewächshäuser in Form von
Halbzylindern.
Gerne werden diese auf einen quaderförmigen Unterbau
gesetzt und dienen dann als Dach. Dann kann man darin auch am Rande
stehen. - Sind die Halbzylinder große Gebäude, kann der Unterbau
wegfallen wie zum Beispiel bei den militärisch genutzten Nissenhütten.
Sie werden bei Wikipedia beschrieben (URL unten). |
... ... ...
|
Ehemalige Lagerhäuser (wie ich vermute) am Hafen
von Rhodos-Stadt, fotografiert im Oktober 2011 |
Beim Körper aus Quader
und Halbzylinder denkt man wohl auch an die amerikanischen "Letter Boxes".
Ein Körper aus einem Halbzylinder
und zwei Viertelkugeln
...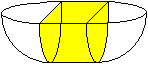 ... ... |
Es gibt Gefäße in Form eines Halbzylinders.
Sie sind aber wegen der Innenkanten schwer sauber zu halten. Deshalb setzt
man gerne Viertelkugeln an die Enden.
Ich denke da an den Schweinetrog aus alten Zeiten. |
Ein
Körper aus zwei Halbzylindern
... ... ...
|
 ... ...
|
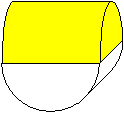
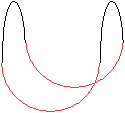
Ist die Grundfläche des Halbzylinders ein Quadrat,
gilt also 2r=h, so kann man zwei Halbzylinder dieser Art um 90° gegeneinander
drehen und aufeinander setzen.
Dann entsteht ein Körper mit einem Gerüst aus
vier Halbkreisen. |
Brechung des Lichts
top
...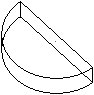 ... ... |
Es gibt für einen Schülerversuch in Physik
einen Halbkreiskörper aus Plexiglas oder auch ein Gefäß
in dieser Form, das Wasser aufnehmen kann.
In einem "Stecknadelversuch" untersucht man die Brechung
des Lichts durch Plexiglas oder Wasser. |
...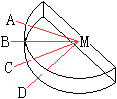 ... ... |
Der Vorteil des Halbkreises liegt darin, dass bei richtiger
Lichtführung die Brechung eines Lichtstrahls nicht beim Eindringen
in den Halbkreiskörper erfolgt, sondern nur beim Austritt am Mittelpunkt
M. |
Praktisch bestimmt man den
Lichtverlauf folgendermaßen.
...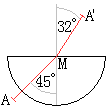 ... ... |
Man legt den Körper auf eine Korkplatte mit einem
Blatt Papier und steckt in die Punkte A und M je eine Nadel. Dann bewegt
man in der Nähe des Punktes A' eine dritte Stecknadel so, dass sie
beim Anpeilen von A und M hinter den beiden Nadeln verschwindet. Man entfernt
die Nadeln und zeichnet den Lichtverlauf nach.
Es ergibt sich das nebenstehende Bild. |
Ziel des Schülerversuches
ist ein Graph, bei dem der Brechungswinkel gegen den Einfallswinkel dargestellt
wird. Die Anfangssteigung ist die Brechzahl.
...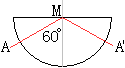 ... ... |
Man beobachtet auch die Totalreflexion.
Im Falle von Wasser z.B. verlässt der Lichtstrahl
ab einem Einfallswinkel von 48,5° es nicht und wird an der Grenzfläche
reflektiert. |
Schwingungen top
Schwingung eines Halbzylinders
... ... ... |
Stellt man einen Körper in Form eines Halbzylinders
auf eine Ebene mit der gekrümmten Fläche unten und tippt auf
eine Spitze, so beginnt der Körper zu schwingen. Im Unterschied zur
Animation kommt er wegen der Reibung allmählich wieder zum Stillstand. |
Es stellt sich die Frage nach einer Schwingungsformel.
Dieses Problem wird auf den Webseiten von Burçin
Ünlü (URL unten) und Dmitry A. Garanin (URL unten) abgehandelt
(Universitätsniveau!).
Für kleine Auslenkungen gilt danach für die
Schwingungsdauer T die Formel
(2pi)/T=[8/sqrt(9pi-16)]sqrt(g/r) oder näherungsweise
2pi/T=0,8073sqrt(g/r).
Dann ist T=2,4843sqrt(r) Sek. (r in Meter).
Es gilt also T~sqrt(r). Je kleiner der Halbkreis ist,
umso schneller schwingt der Klotz.
... ... ... |
Der nebenstehende Klotz hat einen Radius von r=2,5cm=0,025m.
Das führt zu T=0,39 Sek., und das ist etwa die Schwingungsdauer,
die man auch misst. |
Wackelholz
Beim schwingenden Holzklotz denkt man an das Wackelholz
(auch Wackelstein genannt). Der Körper hat die Form eines halben Ellipsoids.
Auf der ebenen Fläche sind zwei kompakte Halbkugeln befestigt, die
die Symmetrie des Körpers aufheben.

von oben
|

von unten
|
Das Besondere ist, dass man das Wackelholz - gekrümmte
Fläche unten - so im Uhrzeigersinn drehen kann, dass es dann nach
einigen Wacklern auf der Stelle im Gegenuhrzeigersinn zurückdreht.
Bei Youtube gibt es neben anderen ein Video, das diese
merkwürdige Bewegung demonstriert (URL unten).
Hersteller meines Wackelholzes: MABRO, Karlsruhe
Halbzylinder
im Internet top
Deutsch
Wikipedia
Zylinder
(Geometrie), Nissenhütte,
Tonnengewölbe,
Tonnendach,
Keltischer
Wackelstein
Youtube
Wackelholz
/ Rattleback
Englisch
Burçin Ünlü (Bogaziçi University
- Physics Department -Türkçe)
Oscillation
of an uniform solid half-cylinder
Dmitry A. Garanin (Lehman College of the City University
of New York)
Oscillation of a Half-cylinder
(.pdf file)
Eric W. Weisstein (MathWorld)
Cylinder,
Horizontal
Cylindrical Segment, Quarter-Tank
Problem
LMNO Engineering, Research, and Software, Ltd.
Volume
of partially full cylindrical, spherical, and conical tanks
Wikipedia
Cylinder
(geometry), Nissen
hut, Barrel vault,
Barrel
roof, Rattleback
Feedback: Emailadresse auf meiner Hauptseite
URL meiner Homepage:
https://www.mathematische-basteleien.de/
© 2012 Jürgen
Köller
top |
 ...
... ...
...




 ...
... ...
...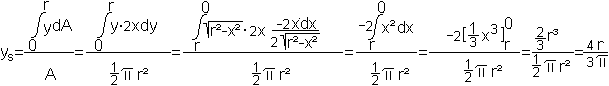
 ...
...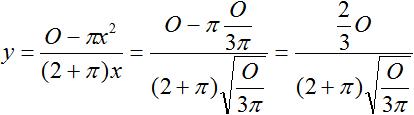
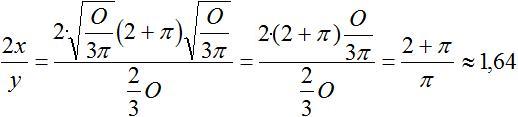
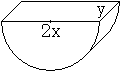
 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...
