|
Was ist das Geobrett?
... ... |
Das Geobrett ist eine Bastelei zur Unterstützung
des Anfangsunterrichtes in Geometrie.
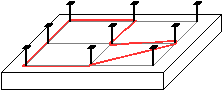
Im einfachen Fall werden neun Nägel in ein Brett
etwa zur Hälfte eingeschlagen, so dass ein 2x2-Quadrat entsteht. Um
die Nägel wird mit einem Gummiband eine Figur gelegt. |
Neben dem Auffinden von Figuren erlaubt das Geodreieck weitere
Tätigkeiten wie Figuren vergleichen, Figuren spiegeln, Figuren verschieben,
Figuren nach einer Vorlage erzeugen, ...
Eine Webseite mit dem Namen
"Mathematische
Basteleien" sollte am Geobrett nicht vorbeigehen.
Da ich keine Unterrichtserfahrung
mit dem Geobrett habe, verweise ich auf die Webseiten unten von Schulpraktikern.
Ich versuche auf dieser Seite,
etwas Hintergrundwissen zu vermitteln. Gut, es sind mehr Spielereien geworden.
Das quadratische
9-Nagelbrett top
1 Verschaffe dir ein nicht zu dünnes Brett.
2 Zeichne ein 2x2-Quadrat auf ein Blatt und klebe es
auf das Brett. Oder zeichne das Quadrat direkt auf das Brett.
3 Schlage an den Eckpunkten der Quadrate neun Nägel
gleich tief ein.
| ... |
Markiere mit einem Gummiband eine Figur............................................................. |
... ... |
Zeichne evtl. die Figur auch in ein Arbeitsblatt ein
oder übertrage einen Entwurf auf das Geobrett. |
... ... |
Ich könnte mir vorstellen, dass die nebenstehenden
einfachen Figuren von Interesse sind. |
Will man mehr Darstellungsmöglichkeiten
haben, sollte man das 9-Nagelbrett zum Beispiel durch das 16-Nagelbrett
ersetzen.
Figuren
auf dem 9-Nagelbrett top
Alle Dreiecke
Gibt man neun Punkte vor, so gibt es nach der Theorie
"9 über 3" oder (9!/(6!*3!)=84 Möglichkeiten, drei Punkte miteinander
zu verbinden.
In 8 Fällen liegen
drei Punkte auf einer Geraden und bilden keine Dreiecke.
... ... |
Die restlichen "Punktdrillinge" bilden acht nichtkongruente
Dreiecke.
In der Zeichnung steht unterhalb der Dreiecke die Anzahl
der unterschiedlichen Lagen, die diese Dreiecke in der Figur haben. |
Die Bilanz 16+16+16+8+8+4+4+4+8=84
zeigt Übereinstimmung mit der Theorie.
Die Dreiecke innerhalb der Figur werden
nach zwei Gesichtspunkten geordnet.
1. Merkmal: Flächeninhalt
... ... |
Der Flächeninhalt der Dreiecke wird durch ganze
Zahlen angegeben.
Als Einheit dient das halbe Quadrat mit A=(1/2)a². |
2. Merkmal: Länge der
Seiten
Die Dreiecke werden von drei verschieden langen Seiten
gebildet, von a, von sqrt(2)*a und von sqrt(5)*a.
... ... |
Unter den Dreiecken stehen die Ziffern "rst".
Sie geben in dieser Reihenfolge die Anzahl der Seiten
einer Sorte an.
r ist die Anzahl der Seiten mit der Länge a, s mit
sqrt(2)*a und t mit sqrt(5)a. |
Der Umfang eines Dreiecks ist dann U=r+s*sqrt(2)+t*sqrt(5).
Alle (?) Figuren
Die zusammenhängenden Figuren
werden geordnet nach der Anzahl der Eckpunkte, dann nach der Maßzahl
des Flächeninhalts, dann nach den Seitenlängen. - Das sind 68
Figuren.
Alle
Rechtecke
... ... |
Das sind alle Rechtecke, die man auf dem Geobrett markieren
kann. |
... ... |
Lässt man auch die Rechtecke zu, die nicht unbedingt
Eckpunkte in den Nägeln haben, so kommen noch neun weitere hinzu. |
Bemerkenswert ist dabei das
innere Quadrat oben rechts in der letzten Zeichnung.
... ... |
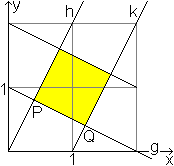Die Seitenlänge ist PQ=(2/5)sqrt(5)a.
Herleitung
Dazu führt man ein kartesisches Koordinatensystem
ein.
Es gelten die Geradengleichungen g: y=-(1/2)x+1 und h:
y=2x und k: y=2x-2.
Aus -(1/2)x+1=2x ergibt sich für P x1=2/3
und dann weiter y1=4/5.
Aus -(1/2)x+1=2x-2 ergibt sich für Q x2 =6/5
und dann weiter y2=2/5.
Dann ist PQ²=(x2-x1)²+(y2-y1)²=(6/5-2/5)²+(2/5-4/5)²=(4/5)²+(2/5)²=20/25
und dann weiter PQ=(2/5)sqrt(5). |
Alle
Strecken
Nach der Theorie gibt es 9*8/2= 36 Möglichkeiten,
neun Punkte miteinander zu verbinden.
Das wird auf meiner Seite Dreieckszahlen
erklärt.
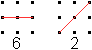
Die Strecken kann man leicht zählen:
... ... |
 ... |
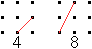In 6+2=8 Fällen liegen 3 Punkte auf einer Geraden.
Es sind für sie 3 Geraden zu zählen.
Das macht 8*3=24 Geraden.
Die restlichen Verbindungen ergeben 4+8=12 Geraden. |
Die Bilanz (4+8)+24=36 zeigt
Übereinstimmung mit der Theorie.
... ... |
Die Strecken einer Sorte bilden markante Figuren. |
Bei meinen Recherchen habe
ich herausgefunden, dass das quadratische 9-Nagelbrett ausführlich
von Horst Steibl (URL unten) untersucht worden ist. Auf seinen Seiten findet
man viele weitere Informationen.
Das ringförmige
9-Nagelbrett top
... ... |
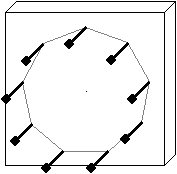Man kann die neun Nägel auch zum regelmäßigen
Neuneck anordnen.
Dann entsteht ein Geobrett, mit dem man die Eigenschaften
eines regelmäßigen Vielecks an einem Beispiel studieren kann. |
Ich
verwende in diesem Kapitel Aussagen meiner Seite
Regelmäßiges
Neuneck.
Figuren
auf dem 9-Nagelbrett top
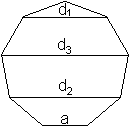
Alle Diagonalen
|
Das Neuneck hat 3 verschieden lange Diagonalen. |
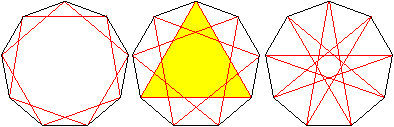
Neun der Diagonalen d1, d2,
und d3 bilden jeweils regelmäßige Sterne.
|
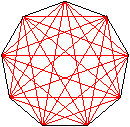
Zusammen sind das 27 Diagonalen.
|
Nach der Theorie gibt es,
wie oben erwähnt, 36 Möglichkeiten, 2 von 9 Punkten miteinander
zu verbinden.
Auf diese Zahl kommt man auch, wenn man zu den 27 Diagonalen
die 9 Seiten des regelmäßigen Neunecks addiert.
Alle
Dreiecke
Gibt man 9 Punkte vor, so gibt es nach der Theorie wie
oben erwähnt 84 Möglichkeiten, 3 Punkte miteinander zu verbinden.
Es gibt 7 nichtkongruente
Dreiecke im Neuneck. Unter den Dreiecken steht die Anzahl einer Sorte.
Die ersten vier Dreiecke enthalten auch eine Neuneckseite
als Seitenlänge. Dann folgen zwei Dreiecke mit d2 als kürzeste
Seite und schließlich das gleichseitige Dreieck aus d3.
Sind die Dreiecke gleichschenklig, kommen sie 9x vor, sonst 18x.
Die Bilanz 9+18+18+9+9+18+3=84 zeigt Übereinstimmung
mit der Theorie.
Alle Vierecke
Gibt man 9 Punkte vor, so gibt es nach der Theorie "9
über 4" oder (9!/(5!*4!)=126 Möglichkeiten, drei Punkte miteinander
zu verbinden.
Durch systematisches Verändern
der Diagonalen gelangt man zu 10 nichtkongruenten Vierecken im Neuneck.
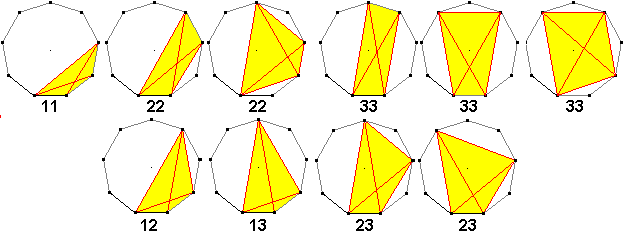Unter den Neunecken stehen die Indices ij der Diagonalenpaare
di dj. Dreht man die Vierecke, so nehmen sie
9 verschiedene, also insgesamt 90 Positionen im Neuneck ein. Die vier asymmetrischen
Vierecke in der zweiten Zeile kann man spiegeln, und das führt zu
36 weiteren Positionen. Insgesamt gibt es also 90+36=126 Vierecke, wie
es die Theorie verlangt.
Alle
Fünfecke
.... .. |
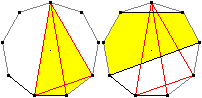Verbindet man in allen Figuren, die Vierecke im Neuneck
enthalten, die freien Punkte, so erhält man alle Fünfecke im
Neuneck.
Links ist ein Beispiel. |
Alle
Sechsecke
.. .... |
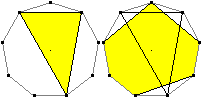Verbindet man in allen Figuren, die die Dreiecke im Neuneck
enthalten, die freien Punkte, so erhält man alle Sechsecke im Neuneck.
Links ist ein Beispiel. |
Alle
Siebenecke
... ... |
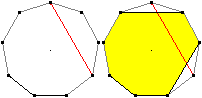Es gibt 27 Diagonalen im Neuneck und genau so viele Siebenecke.....................................
Links ist ein Beispiel................................................................ |
Alle
Achtecke
... ... |
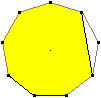Es gibt 9 kongruente Achtecke im Neuneck.
Links ist ein Beispiel.............................................................................. |
Satz von Pick top
Der Satz von Pick beschreibt eine
Methode, den Flächeninhalt eines Vielecks zu bestimmen, wenn die Eckpunkte
Gitterpunkte sind.
Beispiel
... ... |
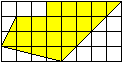Gegeben sei ein unregelmäßiges
Sechseck. .................................................................................. |
... ... |
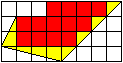Zählt man die Kästchen
aus, so kommt man zu A=13+2+2+1=18 (Flächeneinheiten)...................... |
... ... |
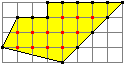Nach dem Satz von Pick kann man zum Flächeninhalt
über die Anzahl i der inneren Punkte und die der Randpunkte r gelangen,
nämlich nach der Formel A=i+r/2-1.
In diesem Beispiel ist i=12 und r=14 und somit A=12+7-1=18
(Flächeneinheiten). |
Geobrett im Internet
top
Deutsch
Daniela Götze, Hartmut Spiegel
"Windmühlen"
- Erfahrungen zur Drehsymmetrie am Geobrett
Horst Steibl
Das
3x3 Geobrett (.pps-Datei)
Wikipedia
Geobrett,
Satz
von Pick
Englisch
A. Bogomolny (Cut-The-Knot)
Geoboard
(Applet), Pick's Theorem
David Eppstein (The Geometry Junkyard)
Euler's
Formula, Proof 10: Pick's Theorem
Eric W. Weisstein (MathWorld)
Pick's
Theorem
Margherita Barile (MathWorld)
Geoboard
MathPlayground.com
Geometry
Board (Applet)
Wikipedia
Geoboard,
Pick's
theorem
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2010 Jürgen Köller
top |