|
Was ist das regelmäßige
Elfeck?
|
Das regelmäßige Elfeck ist ein Vieleck mit
11 gleich langen Seiten,
11 gleich großen Innenwinkeln. |
Das Elfeck heißt auch Hendekagon.
Im Englischen sind die Namen hendecagon und undecagon
üblich. Man findet auch
11 sided figure.
Auf dieser Seite wird das
regelmäßige
Elfeck meist einfach Elfeck genannt.
Größen
des Elfecks top
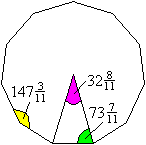
Winkel im Elfeck
 ...
Formeln
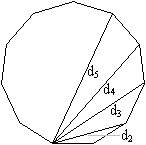
Vier Diagonalen
|
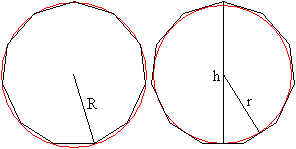
Radius des Umkreises, Radius des Inkreises, Höhe
|
Ist die Seite a gegeben, so lassen sich daraus
der Radius r des Inkreises, der Radius
R des Umkreises, die
Diagonalen d2
,d3
,
d4
und
d5,
die Höhe
h, der Flächeninhalt
A und der Umfang
U
errechnen.
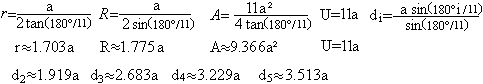Ferner ist h=R+r.
Zur Herleitung der Formeln
Auf meiner Seite Regelmäßiges
Vieleck werden die folgenden Formeln besprochen.
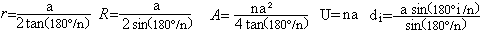
Setzt man n=11, so ergeben sich
die oben stehenden Formeln.
Diagonalen top
|
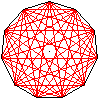
Das regelmäßige Vieleck hat n(n-3)/2 Diagonalen.
Dann hat das Elfeck 44 Diagonalen. |
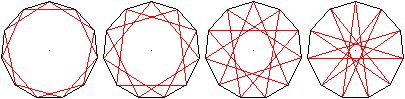
>11 Diagonalen verbinden jeden zweiten, 11 jeden dritten,
11 jeden vierten und 11 jeden fünften Eckpunkt.
>Die Diagonalen bilden vier voneinander unabhängige
Sterne, die Hendekagramme.
>Alle vier Sterne können in einem Zug gezeichnet
werden.
Näherungskonstruktionen
top
Das Elfeck gehört zu den Vielecken,
die man nicht konstruieren kann. Es gibt Näherungskonstruktionen.
Im Bestimmungsdreieck des Elfecks
hat der Winkel an der Spitze eine Größe von (32+8/11)° oder
gerundet 32,7273°.
Ihn kann man näherungsweise
konstruieren.
Erste
Näherungskonstruktion
... ... |
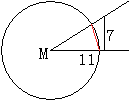Man zeichnet in einen Kreis ein rechtwinkliges Dreieck
mit den Katheten 11 und 7.
Der Mittelpunktwinkel alpha ergibt sich aus tan(alpha)=7/11
zu alpha=32,4712°.
Er ist um 0,78% kleiner als der wahre Winkel (32+8/11)°. |
Zweite
Näherungskonstruktion
... ... |
>Zeichne das gleichseitige Dreieck ABC.
>Halbiere den Winkel CAB. Du erhältst D.
>Zeichne die Senkrechte zu AD durch D. Du erhältst
E. |
>Halbiere AB. Du erhältst F.
>Bestimme den Schnittpunkt von AD und EF. Du erhältst
S.
>Die Strecke CS ist angenähert die Seite des Elfecks.
Überprüfung
Man muss zur Bewertung der Konstruktion die Länge
der Strecke CS berechnen.
... ... |
Dazu legt man besten die Figur in ein kartesisches Koordinatensystem.
Der Einfachheit halber wählt man R=1. |
Man braucht mehrere Rechenschritte.
>Punkt C hat die Darstellung C[1/2|(1/2)sqrt(3)].
>Punkt D hat die Darstellung D[cos(30°)|sin(30°)]
oder D[(1/2)sqrt(3)|1/2].
>Punkt E ist Schnittpunkt der der Geraden AC und
der Senkrechten s durch Punkt D.
s: (y-1/2)/[x-(1/2)sqrt(3)]=-1/tan(30°) oder y=-sqrt(3)x+2
AC: y=tan(60°)x=sqrt(3)x
E: -sqrt(3)x+2=sqrt(3)x oder xE=sqrt(3)/3,
yE=1. Also hat E die Darstellung E[sqrt(3)/3|1]
>Punkt S ist Schnittpunkt der Geraden EF und AD.
EF: (y-0)/(x-1/2)= (1-0)/(sqrt(3)/3-1/2) ... oder y=[2sqrt(3)]/[2-sqrt(3)]x-sqrt(3)/[2-sqrt(3)]
AD: y=tan(30°)x oder y=[sqrt(3)/3]x
S: [2sqrt(3)]/[2-sqrt(3)]x-sqrt(3)/[2-sqrt(3)]=[sqrt(3)/3]x
... oder xS=3/[4+sqrt(3)], yS=sqrt(3)/[4+sqrt(3)]
SC²={3/[4+sqrt(3)]-1/2}²+{sqrt(3)/[4+sqrt(3)]-(1/2)sqrt(3)}²=...
SC=sqrt[7+2sqrt(3)]/[4+sqrt(3)]=0,5643
Nach der Formel oben R=a/(2sin(180°/11)
ist die wahre Seitenlänge a=2sin(180°/11)=0,5635.
Der Fehler ist also (a-SC)/a=0,8%.
Es stellt sich die Frage:
Wie kommt man auf diese Näherungskonstruktion?
1.Schritt
... ... |
Man geht vom Bestimmungsdreieck des Sechsecks aus. Die
halbe Seitenlänge ist kleiner als die gesuchte Seite a, also versucht
man es mit einem Tangentenabschnitt.
Dieser ist etwas zu groß, wie die folgende Rechnung
zeigt.
Nach dem 2.Strahlensatz gilt 1:(1/2)a'=(1/2)sqrt(3):1/2
oder a'=0,5774
Nach der Formel R=a/(2sin(180°/11) oben ist die wahre
Seitenlänge a=2sin(180°/11)=0,5635.
Der Fehler ist also (a'-a)/a=2,47%. |
2.Schritt
... ... |
In einem weiteren Versuch zeichnet man einen Kreis mit
der wahren Seitenlänge um Punkt C.
Der Zufall will es, dass dieser Kreis durch den Halbierungspunkt
F der Strecke AB geht.
Also kann die Strecke CS näherungsweise Seitenlänge
des Elfecks werden. |
Diese Konstruktion und die
Überlegungen dazu gehen auf eine Zuschrift von Lutz Führer zurück.
Symmetrische Figuren aus
Diagonalen
Elfeck im Internet
top
Deutsch
Wikipedia
Elfeck,
Regelmäßiges
Polygon, Polygon,
Konstruierbares
Polygon
Englisch
Eric W. Weisstein (MathWorld)
Hendecagon
("The Canadian dollar coin, nicknamed Loonie, is a hendecagon.")
John Page
Undecagon
Wikipedia
Hendecagon,
Polygon, Hendecagon,
Hendecagram
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
http://www.mathematische-basteleien.de/
©
2005 Jürgen Köller
top |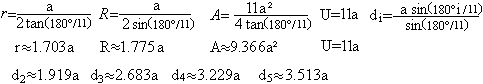
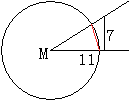