|
What are an Oval and an Egg Curve?
There is no clear definion. Mostly you define:
...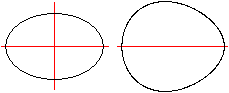 ... ... |
An oval is a closed plane line, which is like an ellipse
or like the shape of the egg of a hen.
An egg curve only is the border line of a hen egg.
The hen egg is smaller at one end and has only one symmetry
axis. |
The oval and the egg shaped curve are convex curves, differentiate
twice and has a positive curvature.
.. .... .... |
You distinguish between the oval, the ovoid and the oval
shape in the same way as between the circle, the figure of the circle and
the sphere. |
Ellipses and
its changings
top
Ellipse
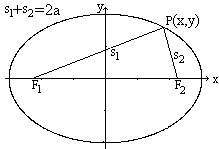
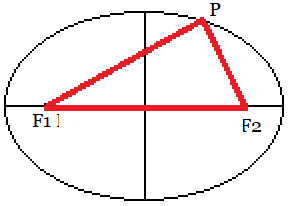
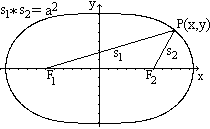
All points P, for which the distances of two fixed points
or foci F1 and F2 have a constant sum, form an ellipse. The ellipse
in the centre position has the following cartesian equation.
The parameters a and b are called lengths of axis.
The ellipse is the formula of a relation.
... ... ...
|
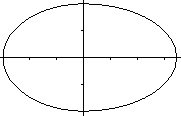
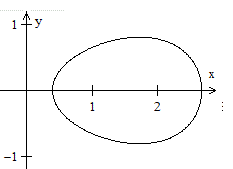
The ellipse on the left has the equation
The constant sum is 2a=6. |
 ... ...
|
You can add two halves of different ellipses to form
a chicken egg. |
A Gardener's
Construction
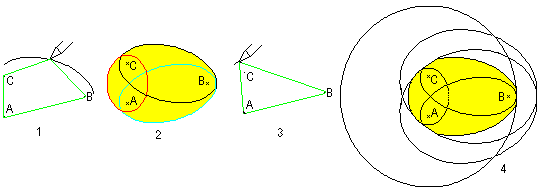 You can draw an egg curve, if you wrap a rope (green) around
an isosceles triangle and draw with taut rope a closed line (1). The rope
must be a little bit longer than the circumference of the triangle. Elllipse
arcs develop, which together form an egg shaped curve (2).
You can draw an egg curve, if you wrap a rope (green) around
an isosceles triangle and draw with taut rope a closed line (1). The rope
must be a little bit longer than the circumference of the triangle. Elllipse
arcs develop, which together form an egg shaped curve (2).
The three main ellipse are totally drawn in a computer
simulation (2,black, red, blue, book 9). You are exacter, if you draw three
more ellipses in the sector of the vertical angles of the triangle angles
to the sides AB, AC und BC (3,4).
Another
Gardener's Construction
... ... ... |
If a gardener wants to create an oval bed, he proceeds
as follows: He drives two stakes into the ground and wraps a ribbon around
them as in the drawing. He sticks a stick, which serves as a pencil, into
the ground and guides it around the stakes. He makes sure that the string
is taut.
This creates an ellipse. |
...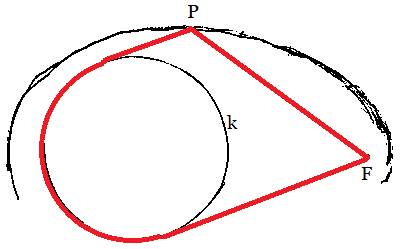 ... ... |
If the stake F1 is replaced by a stake with
a large diameter, the result is a egg shaped curve.
I confirmed this in a small experiment with a medicine
cup, needle, wool thread, ball pen on cardboard. |
Gerhard Rörik has studied
this kind of curves.
...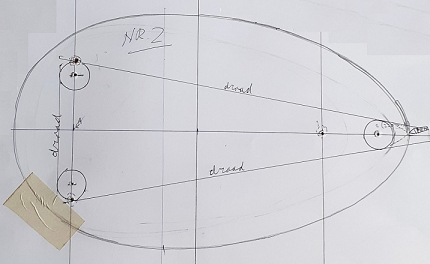 ... ... |
He examined curves around two or three "logs" of different
diameters. |
I thank him for pointing out this method of creating a egg
shaped line.
2022 June
Super
Ellipse
... ... ... |
If you take the exponent 2.5 instead of 2 in the
equation (x/a)²+(y/b)²=1, you get the equation of a super ellipse:
The modulus | | makes sure that the roots are defined.
In the drawing there is a=3 and b=2. |
The Danish author and scientist Piet Hein (1905-1996) dealt
with the super ellipse in great detail (book 4). In particular that the
shape made by rotation around the x-axis can stand on the top, if it is
made from wood. You don't have to use power in contrast to the Columbus'
egg.
The super ellipse belongs to the Lamé curves.
They have the equations
.. .... ....
|
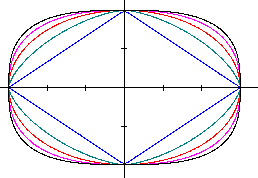
In the drawing there is a=3, b=2 and you substitute n
with 1(parallelogram, blue), 1.5(green), 2(Ellipse, bright red), 2.5 (super
ellipse, red), and 3 (black). |
From
the Oval to the Egg Shape
You can develop the shape of a hen egg, if you change
the equation of a oval a little. You multiply y or y² by a suitable
term t(x), so that y becomes smaller on the right side of the y-axis and
larger on the left side. y(x=0) must not be changed.
The equation of the ellipse e.g. x²/9+y²/4=1
change to x²/9+y²/4*t(x)=1. Here you multiply y² with t(x).
Three examples:
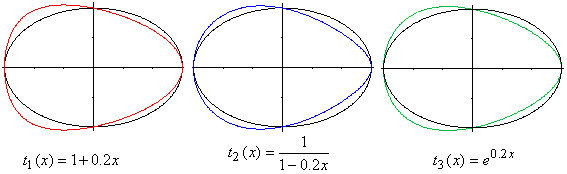
To the red egg shaped curve:
The ellipse is black. The egg curve is red. It lies under
the ellipse on the right side of the y-axis. The term there is larger than
1. The number 4 (=b²) becomes smaller by multiplication of y²/4.
So the curves belongs to ellipses with smaller minor axes. It is under
the black ellipse.
Corresponding you explain, why the red curve lies above
the black ellipse on the left of the y-axis. (You multiply with a number
smaller than 1...)
To the blue and green egg curves:
They have about the same shape, though the equations
are different at first glance.
But:
t2(x)=1/(1-0,2x) can be written as geometric series.
Generally there ist 1/(1-q) = 1+q+q²+..., here is
1/(1-0,2x) = 1+0,2x+0,04x²+...
t3(x)=exp(0.2x) kann be developped as Taylor's series
Generally there is f(x) = f(0)+x*f'(0)+x²*f''(0)+...,
here is exp(0.2x) = 1+0,2x+0,02x²+...
To compare t1(x)=1+0,2*x+0*x².
The three terms t1, t2 und t3 differ in the series
not until in the square term.
| Further there is t1<t3(x)<t2(x).
If you draw the three accompanying egg curves, the red
curves is outside, the green one in the middle and the blue one inside.
Why is the blue egg shaped curve inside the red one?
Smaller minor axes belong to t2(x) compared to t1(x). |
...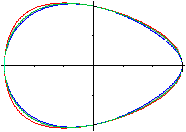 ... ... |
From the Egg to the Triangle
...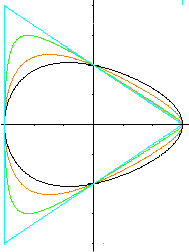 ... ... |
If you substitute the term t(x)=(1+kx)/(1-kx) in the
equation x²/9+y²/4*t(x)=1, you get the curves on the left
for different numbers k.
black: k=0,1 red:
k=0,2 green: k=0,3
blue k=1/3.
The black egg becomes a blue triangle.
The black egg is the same as those of t1(x), t2(x)
oder t3(x) above, because the geometric series (1+0,1x)/(1-0,1x)=1+0.2x+0.02x²+...
correspondend to the first terms.
You get a triangle for k=1/3. a=3 is the major axis.
Proof:
The equations x²/a²+y²/b²*(1+x/a)/(1-x/a)=1
and (x/a+y/a-1)(x/a-y/b-1)(x/a+1)=0 are equivalent. If you simplify both
terms, you get
-b²x³+ab²x²+a²b²x+a²xy²+a³y²-a³b²=0. |
The 3 lines of the triangles are described by the 3 factors
in (x/a+y/b-1)(x/a-y/b-1)(x/a+1)=0
Letter
...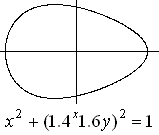 ... ... |
Don M. Jacobs, M.D., from Daly City, USA developped a
nice egg shape by changing the circle equation x²+y²=1 a little:
x² + [1.4^x*1.6y]² = 1.
The egg equation is an exponential equation of the type
t3. This shows this conversion:
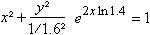 .
. |
Inversion
of an Ellipse in a Circle
 ... ...
|
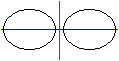
If you reflect an ellipse in a straight line, you get
an ellipse again (on the left).
If you reflect an ellipse in a circle, you get an egg
curve (on the right). |
 |
An inversion is the function of the Argand plane one-one
by reciprocal radii or a reflection in a circle with the radius R. The
centre of the reflection is the origin (0|0). The equation of the function
is z'=R²/z.
More
Curves as Loci of Points top
Cassini Ovals
All points P, for which the distances of two fixed points
or foci F1 and F2 have a constant product, form a Cassini oval.
The Cassini oval has the following Cartesian equation in the centre position
(x²+y²)² - 2e² (x²-y²) - (a²)²
+ (e²)²=0.
2e is the distance of both fixed points, a² is the
constant product.
... ... ...
|
The curve on the left has the equation
(x²+y²)² - 72(x²-y²) - 2800
= 0.
There is e=6, a=8.
|
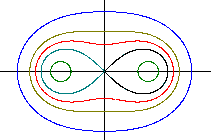 |
This drawing originated from fixing e=6 and substituting
a =10 (blue), 8.5 (grey), 7 ( red), 6 (black) und 4 (green) in the formula. |
Generally said:
If a>[e multiplied by the square root of 2] there
is a egg figure.
If a=[e multiplied by the square root of 2] there
also is an egg figure, but the curvation is 0 on the vertical axis.
If e<a<[e multiplied by the square root of 2] there
is a figure cut into the middle.
If a=e there is a lemniskate.
If a<e there are two ovals.
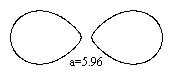
|
The ovals inside with a<e have interesting egg shapes
if the variable a approaches e=6. |
Cartesian
Ovals
All points, for which the simple and the double
distances of two fixed points or foci F1 and F2 have a constant sum,
form a Cartesian oval. The Cartesian oval has the following cartesian equation.
4a²m²((c-x)²+y²)-(a²+m²c²-2cm²x+(m²-1)(x²+y²))²=0
c is the distance of the fixed points and m=2 ("double
distance"). The origin of the coordinate system is the left fixed point.
This long equation is derived with the formulation s1+2*s2=a
and by using Pythagoras' formula twice.
...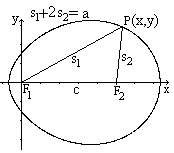 ... ...
|
The distance of the fixed points is c=5 and the sum a=12.
The equation is now
2304((5-x)²+y²) - (3x²+3y²-40x+44)²=0. |
......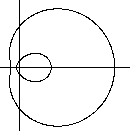 ........ ........ |
The graph from above is incomplete. Surprisingly the
equation 2304((5-x)²+y²)-(3x²+3y²-40x+44)²=0 produces
another curve outside the egg curve. |
......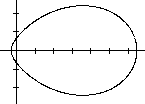 ..... ..... |
If you substitute m=2 with m=2.2, you produce another
egg shape. You keep c=5 and a=12. |
These egg curves go back to Renatus Cartesius alias René
Descartes (1596-1650), therefore the name.
Curves
by Loops
Szegö Curve
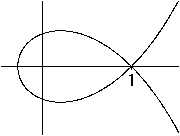
x²+y²=e2x-2
|
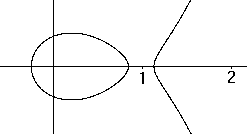
x²+y²+0,02=e2x-2
|
Folium of Descartes
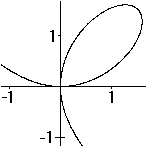
x³+y³=3xy
|
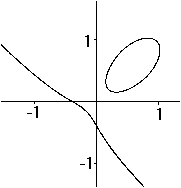
x³+y³+0,06=3xy
|
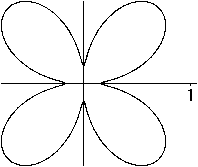
(x²+y²)³-4x²y²
|
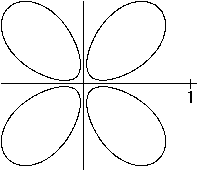
(x²+y²)³+0,001-4x²y²
|
More egg curves this way:
>Trisextrix of MacLaurin y²(1+x)+0,01=x²(3-x)
>Lemniskate of Bernoulli (x²+y²)²-(x²-y²)+0,01=0
>Conchoid of de Sluze 0,5(x+0,5)(x²+y²)-x²+0,02=0
...
|
(Torsten Sillke's idea)
Drawing by
Fritz Hügelschäffer
Transfer the well known drawing of an ellipse with the
help of two concentric circles (on the left) to a two-circle-figure.
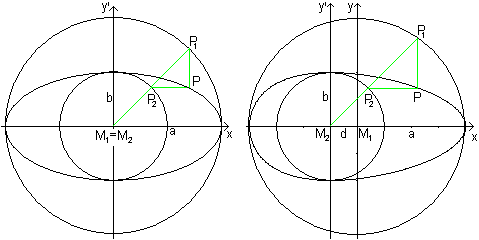
Draw in the order M1,
M2
, P1, P2 ,
and P.
a and b are the radii of the circles, d is the distance
of its centres.
The parameters a, b, c are suitable to describe the egg
shape. 2a is its length, 2b its width and d shows the broadest position.
The equation of the egg shaped
curve is an equation of third degree:
x²/a² + y²/b²[1 + (2dx+d²)/a²]
= 1
b²x²+a²y²+2dxy²+d²y²-a²b²=0
The drawn egg shaped curve has the parameters a=4, b=2
und d=1. The equation is 4x²+16y²+2xy²+y²-64=0.
Second example:
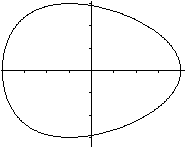
|
In this example there is a=4, b=3 and d=1.
The equation is 9x²+16y²+2xy²+y²-144=0. |
Origin: (11), page 67/68
Granville's
Egg Curve
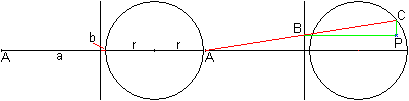
>There is given a line, which starts at point A and lies
horizontally. Then there is a vertical line in the distance of a and a
circle with the radius r being symmetric to the horizontal line in the
distance of a+b (drawing on the left).
>If you draw a line (red) starting at point A, it cuts
the vertical line at B and the circle at C. If you draw then a vertical
line through C and a horizontal line through B (green), they meet at P.
>If the point C moves along the circle, then the points
P lies on a egg shaped curve (animation on the right).
See more: (13), Jan Wassenaar (Granville's egg,
URL below), Torsten Sillke (Granville's egg, URL below)
Mechanical
Egg Curve Construction
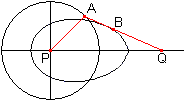 |
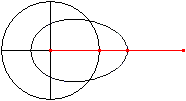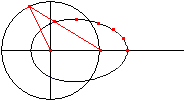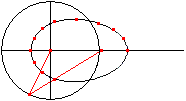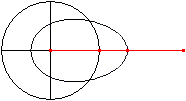
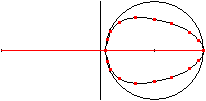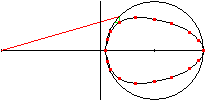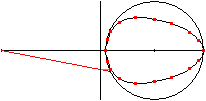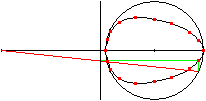
Let P be a fixed point and A a point, which moves on
a circle around P with the radius r=PA.
Link the bar a=QA at A . Its free end Q moves on a horizontal
through P forth and back. The point B on the line AQ with BQ=b describes
an egg shaped curve. |
 |
See more: (12), www.museo.unimo.it/theatrum/macchine/, Jan
Wassenaar (quartic egg curve, URL unten)
Chains of Eggs
top
A Double Egg
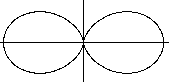 ... ...
|
The polar form r(t)=cos²t produces a double egg
(Münger 1894).
A second equation is r(t)=exp(cos(2t))*cos²(t) (Hortsch
1990). |
Another Double
Egg
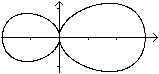
|
The Equation x4+2x²y²+4y4-x³-6x²-xy²=0
produces a double egg. |
There is a wide field of experimenting.
Chains
You can form and combine sinus
curves in such a way, that you get a chain of eggs.
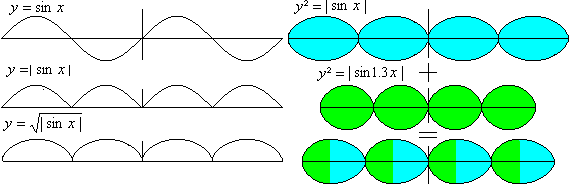
Also polyominals can produce chains (see Torsten Sillke,
URL below).
The equation y² = abs[sin(x)+0.1sin(2x)]
describes a sinus chain more elegant:

(Torsten Sillke)
Egg Curves with
Arcs top
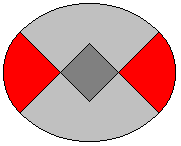
 ... ... |
 ... ... |
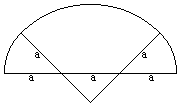
Two small (red) and two big (grey) quarter circles, which
have a square in common, form an oval.
(The angles of the sectors don't have to be 90°.) |
...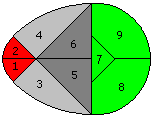 ... ... |
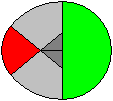
A semi-circle (green), a quarter circle (red) and two
eighth circles (grey), which have a triangle in common, form a second figure.
If you cut the egg in nine pieces, you get the tangram puzzle "The Magic
Egg" or "The Egg of Columbus". |
... ... ...
|
You can generalize the figure: Take a smaller dark grey
triangle. |
...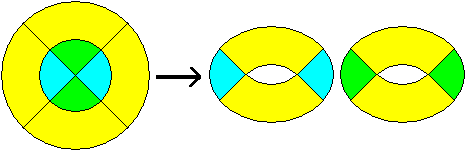 |
Divided and reassembled again |
... ... ... |
Divided and reassembled again.
(14), Seite 122.. |
An
egg inside a pentagon - almost
...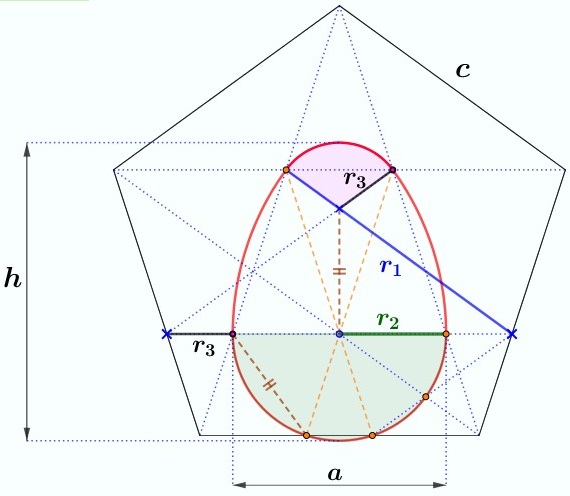 ... ... |
r1 = c
r2 = c(2-phi)
r3 = c(2phi-3)
h =(c/phi)[1+sqrt(7-4phi)]
a = 2c(2-phi)
phi = (1/2)[1+sqrt(5)]
............................................................................................ |
Fernand Marsal sent me this figure
in June 2022, and the formulas also come from him.
Section
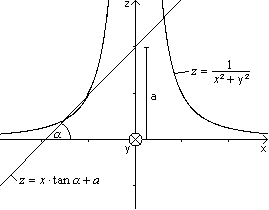
through Rotation Shapes top
If you make a sloping section through
a cone or a cylinder you often get an ellipse as a section line. If you
choose an hyperbolic funnel, you get egg curves in the form of a hen egg.
Hyperbolic funnels are figures, which develop from rotation of an hyperbola
around the symmetry axis.
 ... ...
|
There is the hyperbolic funnel
to f(x) =1/x².
The y-axis is perpendicular to
the x-z-plane in direction to the back.
The straight line shows the section plane perpendicular
to the x-z-plane. |
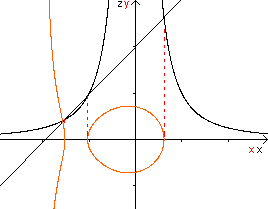 ... ...
|
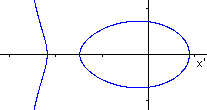
The given plane intersects the hyperbolic
funnel
with three points in the x-z-plane.
If you project the section lines in the x-y-plane you
get the red curves. |
 ... ...
|
You get an egg curve in the section plane. |
Formulas:
If you make a sloping section through
other figures, you get more egg curves.
More Curves top
Equations of 3rd and 4th Degree
...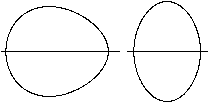 ... ...
|
Equations with the form y²=p(x-a)(x-b)(x-c)... produce
egg curves.
There are two examples on the left:
2y²=(x-1)(x-2)(x-3) and y²=(x-1)(x-2)(x-3)(x-4)
|
The
Folium
 ... ...
|
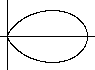
The polar form r(t)=cos³t produces the folium or
wrong Kepler egg. |
A Crooked Egg
"Jedes legt noch schnell ein Ei und dann kommt der Tod
herbei."
"Each still lays a final egg, then comes Death and out
they peg." (Reclam)
... ... ...
|
The polar equation r(t)=sin³t+cos³t produces
a crooked egg ;-). |
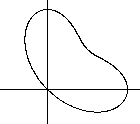
|
Upright
Egg
...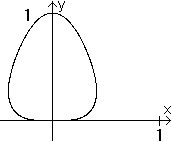
|
Torsten Sillke's egg of Columbus
y^4+10y^2x^2+5x^4 = y |
New
eggs
These egg curves were discovered by Florian Blaschke
(E-Mail from 02.07.2016).
x^1.5-1.5^0.5x+y^2 = 0
|
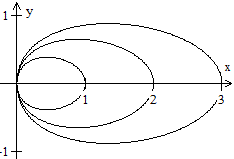
x^1.5-a^0.5x+y^2 = 0 and a=1, 2, 3
|
|
New
egg
...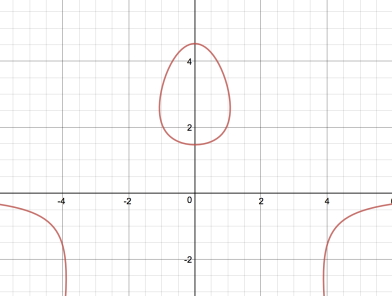 |
This egg curve was discovered by Florian Blaschke (E-Mail
from 23.09.2018)......
2y(x^2)+e*(y-3)^2=6.4
e is the Euler number. |
New
egg
...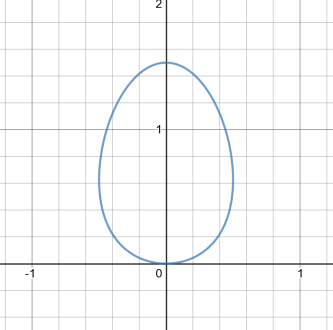 |
Adrian Skovgaard discovered this web page and sent me
another egg.
x^2 = 3*sqrt(2y+1)-2y-3
(Email sent on April 27th 2020) |
New
egg
...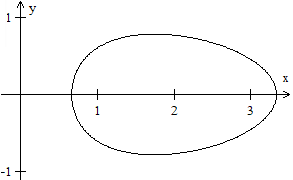 |
Jean-Claude Babois found an equation in which "phi" occurs
from the golden ratio.
y^2+(1/phi)*[sqr( x)-1/phi]^2=(1/10)*(1/phi).
(Email zugesandt am 20.12.2022)
|
New egg
...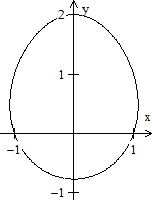 ... ... |
Arthur Bouma sent me, as he wrote, the by far simplest
equation of an egg shaped curve.
x^2+y^2 = 2^y
(Email sent to me on 17.08.2023)
|
3D Egg
...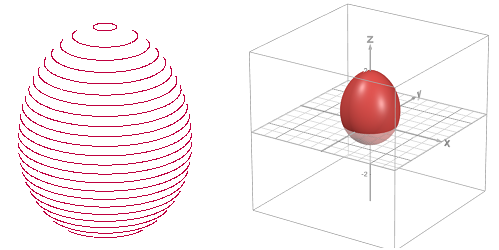 ... ... |
Arthur Bouma had the idea of extending his formula to
the third dimension.
x^2+y^2+z^2= 2^z
Voila, this results in an 3D egg.
The picture on the left was created with the simple drawing
program Winplot of this website, the picture on the right with the
program Desmos 3D Graphing Calculator.
(Email sent to me on 11.07.2024) |
Another
Egg
... |
Joeri Neyt discovered this website and sent a new egg.
cosh(x)/e+y² = x
(Email sent on 15.09.2024) |
References top
English:
(1) Lockwood, E. H.: A Book of Curves.
Cambridge, England: Cambridge University Press, p. 157,
1967.
(2) Martin Gardner: The Last Recreations,
Hydras, Eggs, and Other Math.Mystifications, Springer, New York
1997
German:
(3) Sz.-Nagy, Gyula: Tschirnhaussche Eiflaechen und Eikurven.
Acta Math. Acad. Sci. Hung. 1, 36-45 (1950). Zbl 040.38402
(4) Ulrich/Hoffman: Differential-
und Integralrechnung zum Selbstunterricht, Hollfeld 1975
(5) Martin Gardner: Mathematischer
Karneval, Frankfurt/M, Berlin 1977
(6) Gellert...: Kleine Enzyklopädie
- Mathematik, Leipzig 1986
(7) Wolfgang Hortsch, Alte und neue Eiformeln in der Geschichte
der Mathematik, Muenchen, Selbstverlag 1990, 30S
(8) Gebel und Seifert, Das Ei einmal anders betrachtet,
(eine Schülerarbeit) Junge Wissenschaft 7 (1992)
(9) Hans Schupp, Heinz Dabrock:
Höhere Kurven, BI Wissenschaftsverlag 1995
(10) Gardner, Martin: Geometrie
mit Taxis, die Koepfe der Hydra und andere mathematische Spielereien. Basel:
Birkhaeuser (1997), Deutsche Ausgabe von (2)
(11) Elemente der Mathematik 3 (1948)
(12) Karl Mocnik: Ellipse, Ei-Kurve
und Apollonius-Kreis, Praxis der Mathematik. (1998) v. 40(4) p. 165-167
(13)W. A. Granville: Elements of
the differential and integral calculus, Boston, (1929)
(14) Heinz Haber (Hrsg.): Mathematisches
Kabinett, München 1983 [ISBN 3-423-10121-0]
Egg Curves
on the Internet top
Deutsch
Michael Hinterseher
Eilinien(mit
Klotoiden)
Projekt der Universität Würzburg
Mathematik
rund ums Ei
Wikipedia
Oval
(Geometrie),
Ei-Kurve,
Ellipse,
Superellipse,
Cassinische
Kurve,
Ei des
Kolumbus,
Englisch
André Heck
A
potpourri of mathematical egg curves
CARLOS CALVIMONTES ROJAS
GEOMETRY
OF THE PARABOLA ACCORDING TO THE GOLDEN NUMBER
Chickscope project at the Beckman Institute
Eggmath
Eric W. Weisstein (MathWorld)
Oval,
Cartesian
Ovals,
Cassini
Ovals,
Ellipse,
Cundy
and Rollett's Egg, Mosss
Egg, Lemon,
Superellipse,
Jan Wassenaar
2dcurves
Paul L. Rosin
On
the Construction of Ovals
Richard Parris (Freeware-Programme)
winplot
The MacTutor History of Mathematics archive (Created
by John J O'Connor and Edmund F Robertson)
Cassinian
Oval, Folium,
Cartesian
Oval
Torsten Sillke
Egg
shaped curves
Granville's egg - quartic [Granville 1929]
Cubic curves as perturbated ellipse
Mechanical egg curve construction by a two bar linkage
- a quartic
Polynomials making chains of eggs
Newton's cubic: Elliptic curve
Apollonian cubic
Transforming the ellipse |
Limacon Graphics Gallery
Toric sections - hippopede of Proclus: analyzed by Perseus
The Family r = cos^p(phi) or [Münger
Eggs]
Multifocal Curves - Tschirnhaussche Eikurven
Pivot transform construction of Path-curves
Bezier Curve
References |
Wikipedia
Oval,
Cassini
oval, Superellipse,
Peter
the Great (Fabergé egg), Fabergé
egg, Egg decorating,
Columbus
Egg
Zvonimir Durcevic
CONIC
SECTIONS AND THEIR SPECIAL CASES
Französisch
Robert FERRÉOL (mathcurve)
OVOÏDE,
OVALE
DE DESCARTES, ELLIPSE,
FOLIUM
SIMPLE, OEUF
DOUBLE, Oeuf
d'Ehrhart,
ŒUF
DE GRANVILLE, COURBE
DE ROSILLO, OVOÏDE
Serge MEHL
Ovale,
Ovales
de Cassini
Holländisch
NN (published in: Pythagoras, wiskundetijdschrift
voor jongeren, december 2000)
Een eitje,
zo'n eitje
Pythagoras
De
ei-kromme (page 12)
Usbekistanisch
admin @ arbuz.uz
u cassini.html
Dänisch
Erik Vestergaard
Ellipser
og æg,
Piet
Heins Superellipse
Tschechisch
Jirka Landa
Rovnice vají?ka
- jednoduchá jako Kolumbovo vejce, Velikonocní
speciál (Video)
Japanisch
Nobuo YAMAMOTO
Equation
of Egg Shaped Curve of the Actual Egg is Found, Equation
of Egg Shaped Curve II, Equation
of Egg Shaped Curve III
A.Gärtl, Willi Jeschke,
Torsten Sillke, Gail from Oregon Coast - thanks.
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
2000 Jürgen Köller
top |

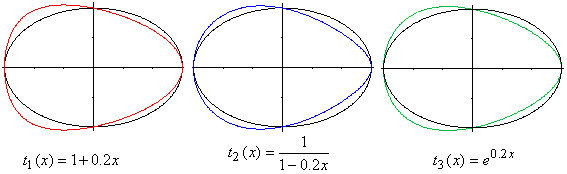
 ...
... ....
....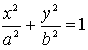
 ...
...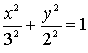
 ...
... ...
... ...
... ...
... ...
...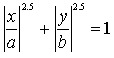
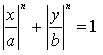
 ....
.... ...
... ...
...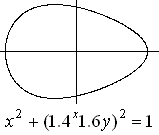 ...
... ...
...
 ...
...
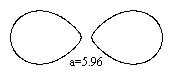
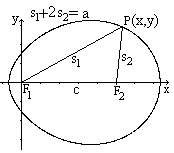 ...
... ........
........ .....
.....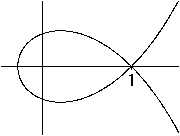
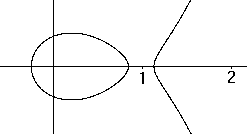
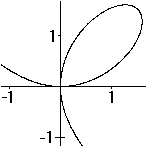
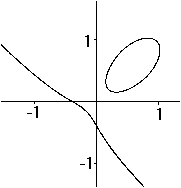
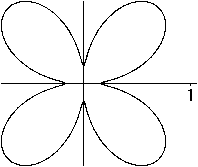
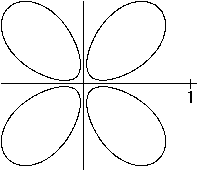

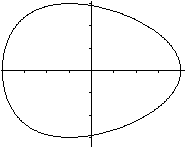


 ...
...
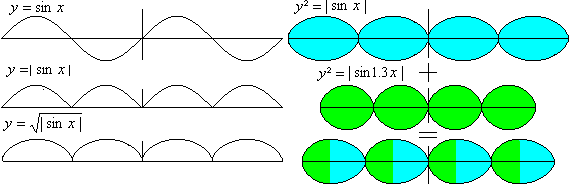

 ...
... ...
... ...
... ...
...
 ...
... ...
... ...
...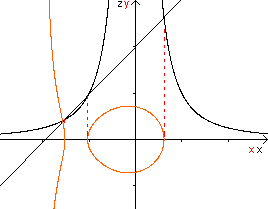 ...
... ...
...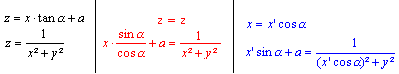
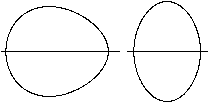 ...
... ...
... ...
...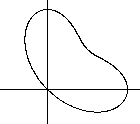

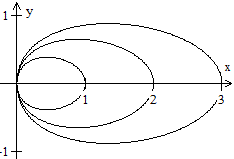



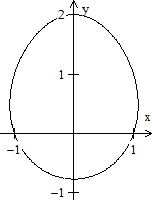 ...
... ...
...