Was ist das Fünfzehnerspiel
..  .. |
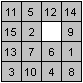Das Fünfzehnerspiel besteht aus 15 Steinen mit den Nummern 1 bis
15. Sie liegen in einem quadratischen Rahmen. Die Steine kann man nicht
herausnehmen und wegen eines freien Feldes nur verschieben. Zu Beginn sind
die Zahlen gemischt (links). Es muss versucht werden, die Ordnung rechts
durch Verschieben zu erreichen. |
..  .. |
Das Spiel heißt auch 14-15-Puzzle oder Boss Puzzle.
Lösen des Puzzles top
 |
Zum Kennenlernen und zum Üben eines Lösungsweges hat sich
ein kleines Modell bewährt, bei dem die Zahlen leicht bewegt werden
können. Das lästige Verkanten der Steine beim Verschieben fällt
weg.
Man zeichnet mit freier Hand auf ein Stück Pappe ein 4x4-Quadrat,
schneidet passende 15 Kärtchen aus, beschriftet sie und legt mit ihnen
das Quadrat aus (links). |
Es gibt viele Möglichkeiten, das Puzzle zu lösen.
... ... |
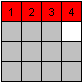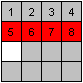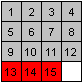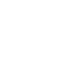Der übliche Weg besteht darin die Zahlen von 1 bis 15 nacheinander
Zeile für Zeile an die richtige Stelle zu bringen.
Eine vollständige Zeile sollte man nie zerstören, zumindest
sollte man die Reihenfolge der Zahlen beibehalten. |
... ...
|
Als erstes bringt man die 1 in die Ecke oben links.
Dazu muss man jeweils vor der 1 ein freies Feld schaffen, damit 1 vorrücken
kann. Es ist günstig andere Zahlen mitzunehmen. |
Dann folgen der Reihe nach die nächsten Zahlen...
... ...
|
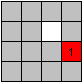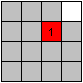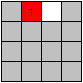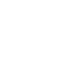
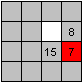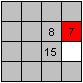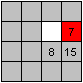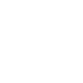
Das ist ein Grundzug, der Kreis: Eine Zahl wird auf einem 2x2-Quadrat
im Kreis bewegt.
Hier wird gezeigt, wie man 7 an die richtige Stelle bringt.
Dreht man im Gegensinn, erreicht auch 8 den richtigen Platz. |
... ...
|
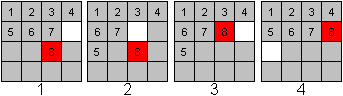
Manchmal steht für das Verschieben eines Steins kein 2x2-Quadrat
zur Verfügung.
Am Beispiel der 8 wird gezeigt, wie man eine (evtl. unvollständige)
Zeile nach links und unten wegschiebt und dann eine Zahl in einem 2x2-Quadrat
bewegen kann. |
... ... |
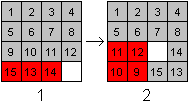Wenn man die dritte Zeile gelöst hat, ist oft auch die vierte
Zeile fertig.
Sonst sind die letzten drei Zahlen in einer falschen Reihenfolge (1).
Dann ist es sinnvoll, die dritte Zeile nach links zu einem 2x2-Quadrat
zu komprimieren (2), um die letzte Zeile dann umzuordnen. |
... ... |
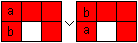Die Lösung hat mehr System, wenn man die Züge in einem 2x3-Rechteck
beherrscht.
Man kann nämlich innerhalb eines 2x3 Rechtecks immer erreichen,
dass zwei beliebige Zahlen (hier a und b) immer an ein Ende gebracht werden
können, auch getauscht (Buch 09). |
Programme top
... ... |
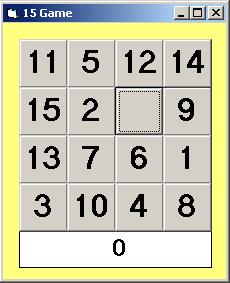Hat man das Puzzle gelöst, kann man sich als nächstes vornehmen,
gemischte Steine mit einer möglichst kleinen Anzahl von Zügen
wieder in die normale Reihenfolge zu bringen. Ich habe dazu ein kleines
Programm in Visual Basic V3 geschrieben, das die Züge simuliert und
zählt. Nach dem Start des Programms sind die Steine schon gemischt.
Man kann das Programm mit Download
in den eigenen Computer holen. Man braucht Vbrun300.dll. |
Im Internet gibt es viele Umsetzungen des 15er-Spiels für den Computer.
Man kann sie online oder offline spielen.
Es gibt aber auch Programme zum Herunterladen, die einen Algorithmus
besitzen, um die kleinste Anzahl von Zügen herauszufinden. Das auf
meiner Webseite angegebene Muster kann in 59 Zügen geordnet werden,
wie das Programm von Ken'ichiro Takahashi (takaken) [URL unten] ermittelte:
9, 1, 6, 9, 1, 14, 12, 1, 2, 15, 11, 5, 1, 2, 15, 7, 9, 4, 10, 3, 13, 9,
3, 10, 8, 6, 14, 15, 4, 3, 7, 11, 5, 1, 2, 4, 3, 8, 6, 14, 15, 12, 4, 3,
8, 6, 14, 15, 12, 8, 6, 7, 11, 6, 7, 11, 10, 14, 15.
Die Berechnung von Lösungen mit möglichst wenigen Zügen
ist ein schwieriges mathematisches Problem (12). Man kennt nur Abschätzungen.
So weiß man heute, dass nach mindestens 80 Zügen das 15 puzzle
gelöst werden kann. (12). Damit werden Computerprogramme mit
der großen Anzahl von Fällen fertig. Sind sie auf der Suche
nach einer Lösung, so können sie nach 80 Zügen abbrechen,
da eine Lösung über 80 uninteressant ist. Das beschleunigt die
Programme.
Etwas Mathematik top
Man betrachte der Einfachheit halber ein 2x2-Quadrat, in dem nur 3
Steine ausgelegt sind. Das freie Feld sei immer unten rechts.
... ... |
Unter dieser Bedingung gibt es drei Möglichkeiten, die Position
der Steine durch Verschieben zu ändern. Sie können geschrieben
werden als 123, 312 und 231. |
... ... |
Aus drei Zahlen kann man 3!=6 Vertauschungen (Permutationen) bilden.
Es gibt noch die Möglichkeiten 132, 213 und 321. Sie führen zu
nebenstehenden Stellungen der Steine, die bei einem Puzzle aber nicht angenommen
werden. |
Wie unterscheiden sich die Permutationen?
Man bildet alle Paare in den Permutationen, bei denen eine größere
Zahl vor einer kleineren liegt ('Inversion').
| Permutation:
123
312
231 |
Alle Paare:
12 13 23
31 32 12
23 21 31 |
Inversionen:
kein Paar
2 Paare: 31 32
2 Paare: 21 31 |
Da die Anzahl der Paare rechts immer gerade ist, heißen diese
Permutationen gerade. (Die geraden Permutationen bilden die alternierende
Untergruppe der Ordnung 3 der symmetrischen Gruppe. Die vorgegebene Menge
muss eine Grundordnung haben.)
Die anderen Permutationen sind ungerade:
| Permutation:
132
213
321 |
Alle Paare:
13 12 32
21 23 13
32 31 21 |
Inversionen:
1 Paar: 32
1 Paar: 21
3 Paare: 32 31 21 |
top
Diesen Sachverhalt kann man auf das 4x4-Quadrat übertragen.
Es gibt 15 Steine, folglich gibt es 15! = 1 307 674 368 000 Permutationen.
Nur die Hälfte der Permutationen ist gerade und wird als Position
angenommen.
Zählt man das leere Feld mit, gibt es 16! = 20 922 789 888 000
Möglichkeiten.
Schiebepuzzles top
..... .....
|
In Italien habe ich ein unlösbares Fünfzehnerspiel entdeckt,
bei dem in der letzten Zeile 14 und 15 vertauscht sind.
Dieses Puzzle ist jedoch unlösbar. Wegen des Paares (15,14) ist
die Permutation (1,2,...,13,15,14) ungerade und lässt sich nicht durch
Verschieben in die gerade Permutation (1,2,...,13,14,15) verwandeln. |
Ich hatte gedacht, dass es Absicht ist
das Puzzle unlösbar zu machen. Nun schrieb mir Martin Beckenkamp im
August 2004, dass er ein Handy mit installiertem 15er-Puzzle besitzt und
dass es "gelöst" anzeigt, wenn die Zahlen in die Reihenfolge
01 02 03 __
04 05 06 07
08 09 10 11
12 13 14 15
gebracht würden. Das entspricht der Anordnung des italienischen Puzzles
oben, bei dem 14 und 15 vertauscht sind.
Die meisten Fünfzehnerspiele, die
man heute kaufen kann, tragen statt Zahlen Bildteile. Man muss die Bilder
finden.
Es folgen zwei Beispiele, Reklame von Mc Donald's und von Kaiser
Bier.
 .........
Übrigens kann man bei Puzzles mit
Rahmen die 15 Steine mit etwas Gewalt herausnehmen. Man muss dazu die Mitte
anheben.
Achterspiel top
... .... |
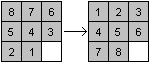Problem:
Man sollte mit möglichst wenigen Zügen
die rückwärts laufenden Zahlen links in die natürliche Reihenfolge
1 bis 8 mit einer Leerstelle unten rechts bringen. |
Das Problem stammt von Henry Ernest Dudeney. Martin
Gardner stellte den Lesern der amerikanischen Zeitschrift "Scientific
American" diese Aufgabe. Zahlreiche Lösungen wurden eingesandt.
... ...
|
... ...
|
... ... |
Ergebnis: Man benötigt nur 30 Züge. - Es gibt 10 Lösungen.
Zwei Lösungen (links und in der Mitte) bilden Paare und sind zueinander
revers. Das erkennt man, wenn man die Züge der zweiten Lösung
rückwärts laufen lässt (rechts). |
... ...
|
Das entsprechende 16er-Spiel ist unlösbar.
Vertauscht man aber 1 und 2, so wird das Puzzle lösbar. Man schafft
es in 70 Zügen: 2, 5, 9, 13, 14, 10, 11, 7, 3, 1, 6, 11, 10, 15, 7
,3, 1, 6, 5, 9, 13, 14, 15, 7, 3, 1, 6, 5, 9, 13, 14, 15, 12, 8, 4, 14,
15, 12, 8, 4, 12, 8, 7, 3, 1, 6, 5, 9, 13, 15, 14, 2, 15, 14, 2, 12, 8,
2, 11, 10, 2, 7, 3, 2, 6, 5, 9, 13, 14, 15. |
Schiebepuzzles
mit verschieden Klötzen top
... ... |
Im Fahrwasser des Fünfzehnerspiels wurden
zahlreiche Puzzles entwickelt, bei denen unterschiedlich große Klötze
verschoben werden mussten.
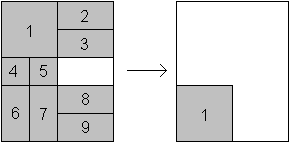
Bei diesem Spiel soll man den quadratischen Klotz
oben links mit möglichst wenigen Zügen nach unten links bringen.
Man braucht mindestens 59 Züge (Lösung
in Buch 07) |
Das Schiebepuzzle heißt Dad's Puzzle.
Zauberturm (Englisch: Tower of Babylon)
top
Im Fahrwasser des Zauberwürfels (Rubik's Cube)
kam in den achtziger Jahren ein Puzzle auf den Markt, das im Prinzip ein
Schiebepuzzle ist.
Man muss 36 Kugeln so ordnen, dass in einer Spalte
6 Kugeln der gleichen Farbe liegen und dass sie darüber hinaus noch
nach Farbtönen geordnet sind. Man kann sie leicht horizontal
verschieben, da sich jeweils sechs Kugeln auf einem Kreisring bewegen
lassen. Die Bewegung in der Vertikalen klappt nur mit einem Trick: Man
kann unten eine Kugel in die Mitte drücken (linker Pfeil), dann rutschen
die Kugeln von oben nach und lassen eine Lücke (rechter Pfeil). Hält
man den Turm horizontal, so kann man die Lücke an jede Stelle bringen
und so Kugeln verschieben. Das reicht zum Lösen. Wegen der Vielzahl
der Kugeln ist das eine stupide Tätigkeit.
Da mein Turm oben eine Schraube hat, kann ich den Turm leicht auseinandernehmen,
die Kugeln ordnen und den Turm dann zusammensetzen ;-). Leider sind dabei
offenbar die "Kugellager" zwischen den Ringen verloren gegangen :-(.
Fünfzehnerspiel im
Internet top
Deutsch:
tan-gram
boss
Wikipedia
15-Puzzle
English:
Alexander Bogomolny (cut-the-knot)
Sam
Loyd's Fifteen, History,
Lucky7,
Happy8,
Slider
Don Taylor
The
14-15 Puzzle
Ed Pegg Jr. (MAA online)
sliding-block
Puzzles
Harry Broeders
15puzzle
Jaap Scherphuis
14-15 puzzle /
Boss puzzle
Jim Loy
The 15 Puzzle (The
possible puzzle; The impossible puzzle)
Karl Hörnell's Applet Center
The 15 Puzzle
Nick Baxter
Sliding Block
Home Page
Ken'ichiro Takahashi (takaken)
15Puzzle
Optimal Solver
Wikipedia
Fifteen puzzle,
Sliding puzzle
Referenzen top
(00) Hermann Schubert: Mathematische Mußestunden, Walter de Gruyter
Verlag Berlin 1941 (1.Auflage 1897)
(01) W.Ahrens: Mathematische Unterhaltungen und Spiele, Leipzig 1918
(02) G.Kowalewski: Mathematica delectans, Band 1 , Leipzig 1921
(03) G.Kowalewski: Alte und neue Spiele, Leipzig 1930 (Nachdruck: Martin
Sändig, Walluf 1978 (ISBN 3-500-19830-9)
(04) Martin Gardner: Mathematical Puzzles & Diversions, New York
1959
(05) Walter Lietzmann: Lustiges und Merkwürdiges von Zahlen und
Formen, Göttingen 1961
(06) Bruno Kerst: Mathematische Spiele, Berlin 1933 (Nachdruck: Martin
Sändig, Wiesbaden 1968)
(07) Martin Gardner: Mathematisches Labyrinth, Braunschweig 1979 (ISBN
3-528-08402-2)
(08) Michael Mrowka: Zauberturm, Teufelstonne und Magische Pyramide,
Niedernhausen/Ts.1981 (ISBN 3-8068-0606-3)
(09) Monika Dewess und Günter Dewess: Summa Summarum, Thun;Frankfurt
am Main, 1986 (ISBN 3-87144-898-2)
(10) Johannes Lehmann (Hrsg.): Rechnen und Raten , Köln 1986 (ISBN
3-7614-0930-3).
(11) L. Edward Hordern: Sliding Piece Puzzles, 249pp, hb, Oxford, England,
1993, Oxford University Press
(12) F. R. W. Karlemo and P. R. J. Östergård : On sliding
block puzzles, Journal of Combinatorial Mathematics and Combinatorial Computing
34 (2000), 97-107
(13) Jerry Slocum & Dic Sonneveld: The 15 Puzzle, Slocum Puzzle
Foundation, 257 South Palm Drive, Beverly Hills, CA 90212, 2006
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
http://www.mathematische-basteleien.de/
©
2000 Jürgen Köller
top |
