|
Was sind geodätische Linien?
... ... ... |
Der kürzeste Weg zwischen zwei Punkten in der Ebene
ist die gerade Linie. Man kennt sie als Luftlinie oder, wie es im Englischen
so schön heißt, "beeline" oder "as the crow flies".
Sie wird zum Problem, wenn man zum Beispiel in den Raum
geht und kürzeste Wege ("geodätische Linien") auf Körperoberflächen
untersucht. |
Darum geht es auf dieser Seite.
Fliege-Spinne-Problem
top
Beim ersten Problem, einem Klassiker der Unterhaltungsmathematik,
ist der Körper ein Quader.
..... ... ...
3D-Bild..
|
In einem Raum mit den Maßen
30' x 12' x 12' (9,14m x 3,65m x 3,65m) sitzt eine Spinne oben rechts auf
einer Seitenfläche in der Mitte, 1 Fuß von der Decke entfernt.
Eine Fliege sitzt unten auf der gegenüberliegenden Wand auch in der
Mitte und 1 Fuß vom Boden entfernt. Die Fliege ist vor Angst gelähmt
und bewegt sich nicht. |
Welches ist der kürzeste Weg,
den die Spinne zurücklegen muss, um die Fliege zu erreichen?
Nahe liegende Lösung
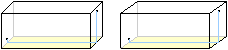
Dieser direkte Weg bietet sich an.
|
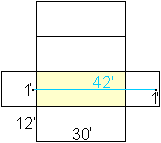
Er beträgt 42 Fuß.
|
Lösung
...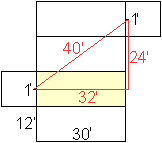 ... ... |
Mit einem Trick gelangt man zu einem kürzeren Weg.
Man betrachtet ein passendes Netz des Quaders und zeichnet
eine gerade Linie als kürzeste Verbindung ein.
Der Weg ist dann kürzer. Nach dem Satz des Pythagoras
ist er 40 Fuß lang. |
...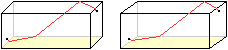 ... ... |
Es gibt noch eine zweite, spiegelbildliche Lösung.
Man nennt die Linie der Länge
40' geodätisch. Sie besteht aus fünf Streckenabschnitten, lässt
sich aber auf eine Strecke zurückführen.
Martin Gardner beschreibt
das Rätsel in einem Artikel über Dudeney ("Henry Ernest Dudeney:
Englands größter Rätselerfinder") in seinem unten genannten
Buch (1), Seite 73ff.
Dudeney veröffentlichte es 1903 in einer englischen
Zeitung. Es wurde bekannt, als es 1905 in der "Daily Mail" abgedruckt wurde.
Kotani's Ant Problem
top
...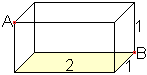 ... ... |
Eine Ameise befindet sich oben, links, vorne in einem
1x1x2-Quader.
Sie soll auf einem möglichst kurzen Weg in die gegenüberliegende
Ecke unten, rechts, hinten krabbeln.
Welchen Weg muss sie nehmen? |
...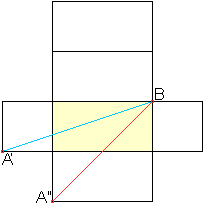 ... ... |
Lösung:
Man klappt wieder den Quader auf, A fällt auf A'
oder A''.
A''B=sqrt(2²+2²)=sqrt(8) und A'B=sqrt(3²+1²)=sqrt(10)
Der erste Weg A''B ist also kürzer. |
Das Problem ist nur aufwendig
zu lösen, wenn man Punkt A an eine beliebige Stelle legt und dann
nach dem am weitesten entfernten Punkt B fragt. Diese Erweiterung ist unter
dem Namen Donald Knuth's Ant Problem unten beschrieben.
Fliege-Honig-Problem
top
Das folgende Problem stammt auch von Dudeney [(1), Seite
73ff.].
... ... ... |
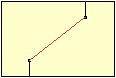
Ein Glaszylinder ist 4 cm hoch und hat einen Umfang von
6 cm.
Auf der Außenseite, 1 cm vom Boden entfernt, sitzt
eine Fliege. Auf der anderen Seite genau gegenüber und innen, befindet
sich ein Honigtropfen.
Welches ist der kürzeste Weg, den die Fliege krabbeln
muss, um den Honig zu erreichen? |
Lösung
... ... ...
|
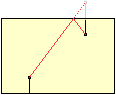
Angenommen, der Honigtropfen sitzt auch außen.
Man rollt den Mantel des Zylinders ab.
Die gerade Linie ist der kürzeste Weg. |
... ... ...
|
Nun sitzt der Honigtropfen aber innen.
Deshalb muss die Fliege einen anderen Weg nehmen.
Sie muss bis zum Rand auf das Spiegelbild des Tropfens
zumarschieren und vom Rand ab auf einer geraden Linie zum Tropfen. - Der
kürzeste Weg ist 5cm lang. |
Es folgen noch drei Anmerkungen
zur kürzesten Linie auf einem Zylindermantel.
1
...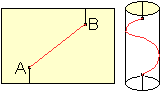 ... ... |
Fliege und Honig werden ersetzt durch die Punkte A und
B.
Die Punkte liegen sich gegenüber. Deshalb gibt es
zwei gleiche Wege in Form von Spiralen mit halbem Umlauf. |
2
...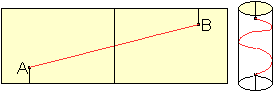 ... ... |
Man kann auf dem Mantel auch einen geraden Weg finden,
der einen Umlauf mehr erfordert. Dazu dient das nebenstehende Netz, das
man doppelt rollen muss. |
3
...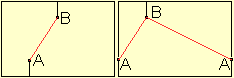 ... ... |
Es sei der Fall gegeben, dass sich die Punkte A und B
nicht gegenüberliegen, sondern nur um eine Vierteldrehung gegeneinander
versetzt sind. Dann ist es günstig, den Mantel an der Stelle A aufzuschneiden.
Somit liegt A an den beiden Rändern des aufgerollten Mantels. Es gibt
zwei verschieden lange Wege von A nach B. |
Bei den hier beschriebenen
geraden Linien zwischen A und B handelt es sich um geodätische Linien.
Sie können unterschiedlich lang sein. Wegen der beliebigen Zahl der
Umläufe gibt es auch beliebig viele geodätische Linien auf einer
Zylinderoberfläche. Von Interesse sind die Linien mit der kleinsten
Länge, die "Kürzesten".
Umlauf um die
Kegelspitze
top
Neben dem Zylinder gehört der gerade Kreiskegel
zu den Körpern mit einem ebenen Netz.
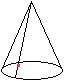
Da kann man sich die folgende Frage stellen, die nicht
in eine Geschichte gekleidet werden soll.
... ... ...
|
Gegeben ist ein Startpunkt auf einem Kegel.
Wie groß ist der kürzeste Weg, der um die
Spitze herum und zurück zum Ausgangspunkt führt?
Es bietet sich der Weg rechts an. |
... ... ...
|
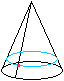
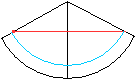
Lösung
... ... ...
|
Das ist aber nicht der minimale Weg, wie das Netz des
Mantels zeigt.
Rollt man den Kegelmantel ab, so ist die rote Linie der
kürzeste Weg.
Das führt zur Schlaufe rechts. |
...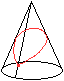 ... ... |
Grenzen der Lösung
... ... ... |
Ist der Kegel flacher und der Mantel ein Kreisausschnitt
mit einem Winkel gleich oder größer als 180°, so gibt es
keine Schlaufe mehr als kürzesten Weg. Der Weg auf einer Falllinie
und zurück könnte als Minimalweg angesehen werden, aber er führt
nicht mehr um die Spitze herum. |
Siehe auch (2), Seite 80f.
Das Besondere an diesem Kegel-Problem
besteht darin, dass es hier um geschlossene geodätische Linien geht.
Die beiden Punkte, die zu verbinden sind, fallen zusammen.
Das allgemeinere Problem geodätischer Linien auf
Kegelmäntel wird auf der Webseite von Mark L. Irons (Geodesics on
a Cone, URL unten) ausführlich untersucht.
Einfach
geschlossene geodätische Linien eines Würfels top
In dem unten genannten Buch von Steinhaus (3) wird der
Würfel auf geschlossene geodätische Linien hin untersucht.
Zur Einführung weist Steinhaus darauf hin, dass
man sich die geodätische Linie als Gummiband vorstellen kann, das
man um den Würfel legt. Wichtig dabei ist, dass der Würfel glatt
ist und keine Reibung auftritt.
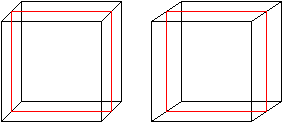
Dann gibt es im wesentlichen zwei Möglichkeiten.
Die linke Schlinge ist trivial.
Die rechte Umschlingung ist ein Sechseck und erfasst
alle Quadrate des Würfels. Steinhaus zeigt durch eine Rechnung, dass
die geschlossene Linie minimal wird, wenn die Abschnitte parallel zu Flächendiagonalen
des Quadrates liegen, wie in der Zeichnung beachtet.
Im Sonderfall wird das Sechseck regelmäßig.
Das Gummiband verläuft dann durch Kantenmitten.
...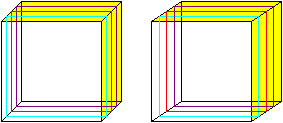 ... ... |
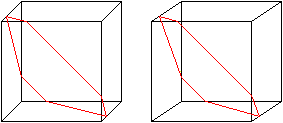
Bleibt man im Bild des Gummibandes, so gibt es im trivialen
Fall beliebig viele weitere parallel liegende Bänder, die dann vier
Quadrate bedecken. |
Da es drei gegenüber liegende Paare von Quadraten gibt,
gibt es somit auch drei Scharen von geodätischen Linien.
...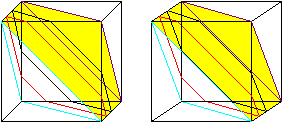 ... ... |
Im Falle der Sechsecke bleiben zwei gegenüber liegende
Eckstücke frei und damit je drei Halbquadrate, während ebenso
viele Halbquadrate bedeckt werden. |
Da der Würfel vier gegenüberliegende Ecken hat,
gibt es auch vier Scharen von geodätischen Linien dieser Art.
Insgesamt hat der Würfel also sieben Scharen von
einfach geschlossenen geodätischen Linien.
Siehe auch (3) Seite 86ff.
Großkreis
einer Kugel top
Bisher wurden nur Körper betrachtet, deren Netze
in der Ebene ausgebreitet werden können, die also abwickelbar sind.
Da konnten die geodätischen Linien zu zwei Punkten auf Strecken zurückgeführt
werden. Das gelingt nicht bei der Kugel.
...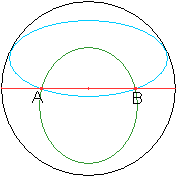 ... ... |
Gibt man auf der Kugeloberfläche zwei Punkte A und
B vor, kann man die Kugel so betrachten, dass die beiden Punkte auf dem
"Äquator" liegen. Der Äquator erscheint in der Zeichnung
als Strecke und Durchmesser der Kugel.
Sucht man andere Kreise als Wege (zwei sind eingezeichnet),
so haben sie alle einen kleineren Durchmesser als der Äquator und
ihre Bögen über AB sind länger.
Der Äquator ist der kürzeste Kreis-Weg. |
Man nennt ihn Großkreis. Sein Durchmesser stimmt mit
der Kugel überein und sein Mittelpunkt ist der Kugelmittelpunkt.
Die übrigen Kreise auf der Kugeloberfläche nennt man Kleinkreise.
Das Wort Äquator ist
schon ein Hinweis darauf, dass das Problem "kürzester Weg auf Kugeln"
für die Erdkugel eine praktische Bedeutung hat. Man sollte meinen,
dass sich Schiffe und Flugzeuge, die große Entfernungen zurücklegen,
immer längs Großkreisen (Orthodromen) weiter bewegen.
Das scheint nur bedingt der Fall zu sein. Für eine Route spielen auch
andere Faktoren eine Rolle.
... ... ... |
In diesem Zusammenhang sind Routen in Form von spiralförmigen
Loxodromen (shrub lines) interessant, weil bei ihnen eine bestimmte Richtung
mit dem Kompass eingestellt und beibehalten wird.
So wurde zumindest früher auf Schiffen navigiert. |
Zum
Begriff der geodätischen Linie top
Die Beispiele auf dieser Seite
belegen es: Die Verbindungslinien zwischen zwei Punkten in der Ebene
und auf den Oberflächen abwickelbarer Körper sind geodätisch,
wenn sie gerade sind oder auf gerade Linien zurückgeführt werden
können.
Das kann man auf die Kugel- und
beliebige Körperoberflächen übertragen: Verbindet man zwei
Punkte, so sind die Linien dann geodätisch, wenn sie auf infinitesimal
kurzen Strecken gerade sind. Dazu kommt noch, dass man sich entlang der
Linien einen infinitesimal schmalen, ebenen Streifen vorstellen können
muss (4).
...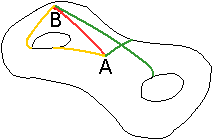 ... ... |
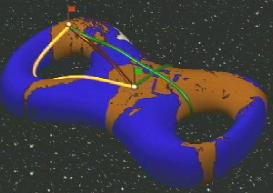
Konrad Polthier von der Freien Universität Berlin
hat einen Videofilm ins Internet gestellt, in dem man beobachten kann,
wie sich drei geodätische Linien auf einem doppeltorus-artigen Körper
bilden.
Man denke beim Anblick dieses Videos
an die obigen Aussagen. |
Der Begriff der geodätischen
Linie ist ein Begriff der klassischen Differentialgeometrie. Die Definition
lautet:
"Die Kurven auf einer Fläche, deren geodätische
Krümmung verschwindet, sind geodätisch."
Es erfordert offenbar ein tiefergehendes Fachwissen,
um diese Definition mit Inhalt zu füllen.
Man gehe einmal auf die MathWorld- oder Wikipedia-Seiten
Geodäte
bzw. Geodesic
(URL unten).
Ausklang

Zweifellos der kürzeste Weg ;-)
Mehr über Irrgärten
hier
Die Seite enthält Tipps von Torsten Sillke
Geodätische
Linien im Internet top
Deutsch
ADG – Fachverband der Geometrie
SPINNE
UND FLIEGE (.pdf-Datei)
Wikipedia
Geodäte,
Orthodrome,
Loxodrome,
Sattelfläche
Englisch
Caltech
The
Straightest Lines in Curved Space and Time
enriching mathematics (University of Cambridge)
The
Spider and the Fly, - A shortest route on The
Dodecahedron, Flight
Path
Eric W.Weisstein (MathWorld)
Spider
and Fly Problem, Geodesic,
Geodesic
Curvature, Wiedersehen
Pair
Jeff Erickson (Ernie's 3D Pancakes)
Shortest
paths on PL surfaces
Karen Franco (Bill Casselman's Home Page)
Spherical
Geometry: Exploring the World with Math
Konrad Polthier (Freie Universität Berlin, Germany)
Introduction
to Geodesics (video)
Man muss Geduld beim Herunterladen des Videos haben. |
 |
Mark L. Irons
Geodesics
on a Cone
Movable Type Ltd
Vincenty
formula for distance between two Latitude/Longitude points
Robert Hunt
Time
and motion
Wikipedia
Great
circle,
Great-circle
distance, Geodesic,
Rhumb
line
Youtube (Physics Videos by Eugene Khutoryansky)
Die
Schönheiten der Geodäten
Referenzen top
(1) Martin Gardner: Mathematische Rätsel und Probleme,
Braunschweig 1968
(2) Ferenc Molnár: Spinne und Fliege, in "Mathematisches
Mosaik", Köln 1977 [ISBN 3-7614-0371-2]
(3) Hugo Steinhaus: 100 Aufgaben, Leipzig-Jena-Berlin,
1968
(4) W.Gellert (Hrsg.): Mathematik, Leipzig 1986
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2007 Jürgen Köller
top |

 ...
... ...
...


 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...
 ...
... ...
... ...
... ...
... ...
...