|
Was ist eine Tetrade?
Schreibt man die natürlichen Zahlen von 0 bis 15
im binären Ziffernsystem auf, so erhält man vierstellige Zahlen,
wenn man auch die Vornullen mitzählt. Diese Zahlen heißen Tetraden.
Heute heißen sie Nibbles.
Das sind die 16 Tetraden:
|
0000
|
0001
|
0010
|
0011
|
0100
|
0101
|
0110
|
0111
|
1000
|
1001
|
1010
|
1011
|
1100
|
1101
|
1110
|
1111
|
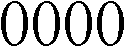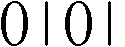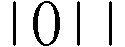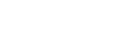
Die Ziffer 1 wird oft als Strich geschrieben. Das ist
an unseren Schulen üblich, denn so wird deutlich, dass das binäre
System gemeint ist. Dieser Luxus geht amerikanischen Schülern ab,
denn sie schreiben schon die Zehnerziffer 1 als Strich.
Man kann die Tetraden auch als "Kombination
von 2 Elementen 4.Ordnung" ansehen. Das heißt, dass man die beiden
Zeichen 0 und 1 auf alle möglichen Arten auf vier Plätze verteilt.
Man kann auch vier Münzen werfen.
Dann liegen entweder Wappen oder Zahl oben. Die möglichen Ergebnisse
gibt man durch Tetraden an.
16er-System top
Es heißt auch Sedezimalsystem.
Viele kennen vielleicht aus den Anfangsjahren der Computerei
das 16er System. Es ist gut geeignet Bitmuster zu beschreiben. Man kann
es einführen, indem man den 16 Tetraden Zahlzeichen zuordnet. Man
wählt die zehn Ziffern und die Buchstaben A bis F. Das sind 16 Ziffern.
0000
0
|
0001
1
|
0010
2
|
0011
3
|
0100
4
|
0101
5
|
0110
6
|
0111
7
|
1000
8
|
1001
9
|
1010
A
|
1011
B
|
1100
C
|
1101
D
|
1110
E
|
1111
F
|
Will man nun eine Zahl wie 9A3F ins
Zehnersystem übertragen, muss man die Ziffern in die folgende Tabelle
eintragen:
|
...
|
4096-er
9
|
256-er
A
|
16-er
3
|
1-er
F
|
Die Zahl 9A3F ist dann 9*4096++10*256+3*16+15=39487.
Soll umgekehrt eine Zahl wie 49152
in das 16er-System überführt werden, muss man die Zahl mit a*4096+b*256+c*16+d
zerlegen. Das ist hier einfach. Es gilt nämlich 49152=12*4096. Die
Zahl ist C000. (C64-Benutzer kennen diese Zahl von SYS 49152.)
Die
Armbandaufgabe
top
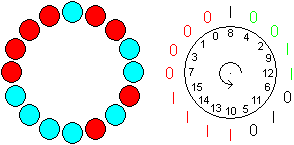
In Gardners Buch gab Dr.Matrix bei Tiffany ein Armband
in Auftrag, das aus 16 Kugeln bestehen sollte, zur Hälfte aus Perlen
und zur Hälfte aus Jade. Das Besondere sollte sein, dass sie in einem
vollen Umlauf alle 16 Quadrupel aus 0 und 1 enthalten sollte.
... ... ...
|
Eine Lösung zeigt die Zeichnung links, einmal dargestellt
mit roten und blauen Perlen und dann die Erklärung mit Tetraden. |
Es gibt noch weitere Lösungen. Man findet sie, wenn
man bedenkt, dass sowohl Blöcke aus vier Nullen und vier Einsen (rot)
vorkommen müssen und auch Paare (grün). Sie müssen aber
nicht wie oben nebeneinander stehen.
Alle Lösungen am Ende
Farbkontakt-Puzzle
top
...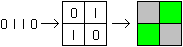 ....... ....... |
Man kann zu jeder Tetrade einen Spielstein herstellen.
Man schreibt die vier Ziffern in zwei Zeilen in ein 2x2-Quadrat und färbt
die Felder grau für 0 und grün für 1. |
... ... ...
|
So erhält man 16 Steine, die ein 4x4-Quadrat bilden
können.
Sie sind hier in der natürlichen Reihenfolge 0 1
2 3 4 5 6 7 8 9 A B C D E F angeordnet. |
Aufgabe ist es die Steine so umzulegen,
dass sie sich in den gleichen Farben berühren. Das ist die Domino-Eigenschaft.
Die Steine dürfen nicht gedreht werden.
... ... ...
|
Hier ist eine Lösung. Sie hat die Notation 2 5 B
3 9 7 F E 4 C D A 0 1 6 8. ................ |
Das Puzzle stammt von C.J.Bouwkamp und wird in Buch 2 von
Slocum Botermans auf Seite 165 beschrieben. Es heißt
auf Englisch
Pantactic Puzzle (Pantaktisches Puzzle, = Alle-Formationen-Puzzle).
Es gibt 50 Lösungen. Darunter
sind 16 Lösungen zylindrisch in beiden Richtungen. Das heißt:
Formt man aus dem 4x4-Quadrat-Blatt nacheinander mit vertikaler und
horizontaler Achse einen Zylinder, so stoßen gleiche Farben aufeinander
(Buch 3). Die Lösung oben ist so eine "toroidal"e Lösung.
Auf meiner Seite Magische
Quadrate werden die Zylinder (mit anderer Bedeutung) gezeichnet.
Wer mit dem Farbkontakt-Puzzle spielen
will, kann es leicht aus Pappquadraten bauen. Man sollte auf die Steine
die Zahlen schreiben, damit man sie nicht aus Versehen dreht.
Ich biete hier zum Herunterladen
eine Umsetzung des Puzzles für den Computer an. Es wurde mir freundlicherweise
von R.Horster zur Verfügung gestellt. Es hat zip-gepackt 155 kByte.
Astles
Pantaktisches Quadrat top
... ... ...
|
Ein 5x5-Quadrat hat 16 Quadrate
vom Format 2x2...
(Übrigens gibt es in der Figur
insgesamt 1²+2²+3²+4²+5²=55 Quadrate unterschiedlicher
Größe.) |
Da liegt die folgende Aufgabe nahe:
Verteile die 16 Tetraden auf die 2x2-Quadrate.
... ... ... |
Hier ist eine von 16 Lösungen. Die Null wird durch
ein graues Quadrat und die Eins durch ein grünes Quadrat dargestellt.
Notation: C 9 3 6 0 5 F A 2 4 D B 8 1 7 E. |
Quelle: (3) Jaques Haubrich
Hyperkubus top
... ... ...
|
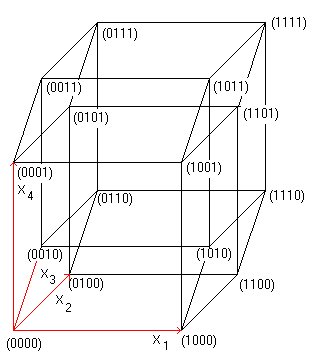
Fasst man die Tetraden als Koordinaten von 16 Punkten
auf, zeichnet die Punkte in ein Koordinatensystem und verbindet sie passend,
so ergibt sich die Darstellung eines vierdimensionalen Würfels.
Der Hyperkubus wird an einer anderen Stelle
meiner Homepage beschrieben. |
Tetraden-Codes top
Soll ein Computer Zahlen verarbeiten, müssen sie
mit 0 und 1 kodiert werden. Man sollte meinen, dass man eine Zahl wie 234
dazu einfach ins Zweiersystem überführt: 234=128+64+32+8+2=11101010.
Das ist aber nicht der Fall.
Man verwendet zum Beispiel beim BCD-Code Tetraden: Man
setzt im Falle 234 für 2=0010, für 3=0011, für 4=0100.
So ergibt sich 234=0010 0011 0100.
Weitere Informationen bekommt man über die Linkliste
unten.
Lösung top
...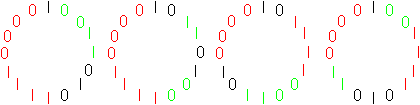 ... ... |
Das sind vier Lösungen.
Bildet man das Komplement oder, anders ausgedrückt,
ersetzt man 0 durch 1 und 1 durch 0, so gibt es vier weitere Lösungen. |
zurück
Tetraden im Internet
top
Deutsch
EDEMI (Einführung in die Digitaltechnik mit Hilfe
elektronischer und multimedialer Informationsquelle)
Binäre
Codes und Code-Umsetzer
Ralph Stenzel
Spielcomputer LOGIKUS
Auf meiner Webseite Zweiersystem
wird demonstriert, wie man sich einstellige Zahlen im Zweiersystem anzeigen
lassen kann.
T.Paul Fischer
Bits,
Nibbles und Bytes
Wikipedia
Nibble,
BCD-Code
Englisch
Mathematica
Binary
Wheels
Wikipedia
Nibble,
Binary-coded
decimal
Referenzen top
(1) Martin Gardner: Die magischen Zahlen des Dr. Matrix,
Frankfurt a.M., 1987 [ISBN 3.8105-0713-X], Seite 34 ff.
(2) Pieter van Delft, Jack Botermans: Denkspiele der
Welt, München 1980, Seite 165
(3) Jaques Haubrich: Pantactic Patterns and Puzzles,
CFF 34 (Dort findet man weitergehende Literatur.)
Eine Einführung in das
Zweiersystem findet man auf meiner Seite
Zweiersystem.
Ich bedanke mich bei Torsten
Sillke für etliche Tipps.
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2003 Jürgen Köller
top |
 ...
... ...
... ...
... ...
... ...
... ...
... ...
...