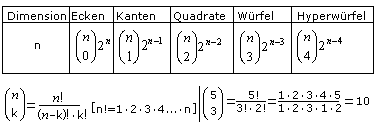|
Was ist ein Hyperkubus?
Der Hyperkubus ist der vierdimensionale Würfel.
Unsere Vorstellungskraft reicht nicht aus, um sich die
vierte Dimension und speziell den Hyperkubus als Ganzes vorzustellen.
In Analogie zum Übergang vom Quadrat zum Würfel
kann man sich dem Hyperkubus vom Würfel aus von verschiedenen Seiten
nähern und wird so mit ihm vertraut.
Er heißt auch Tesserakt, Hyperwürfel oder Achtzell.
Schrägbilder
top
... ... |
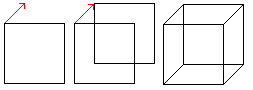Verschiebt man ein Quadrat parallel in der Ebene und
verbindet entsprechende Ecken, so entsteht das Schrägbild eines Würfels. |
... ... |
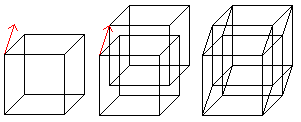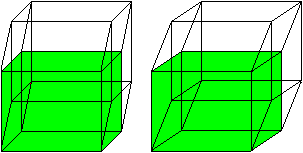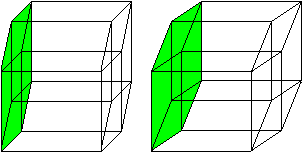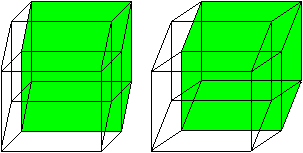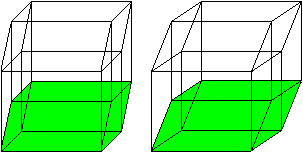
Verschiebt man einen Würfel parallel im Raum und
verbindet entsprechende Ecken, so entsteht das Schrägbild eines Hyperkubus. |
Der Hyperkubus hat 16 Ecken (aus 2 Würfeln hervorgegangen)
und 32 Kanten (2 Würfel und Verbindungslinien).
... ... |
|
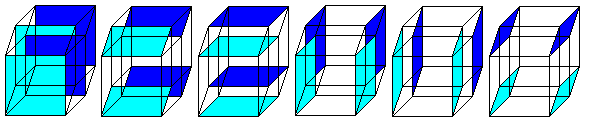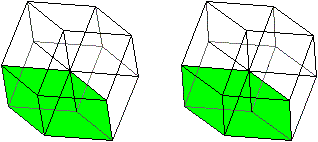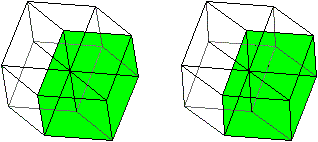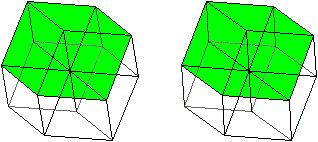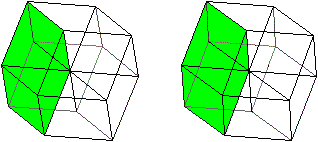
Der Hyperkubus hat 24 Quadrate.
... ...... |
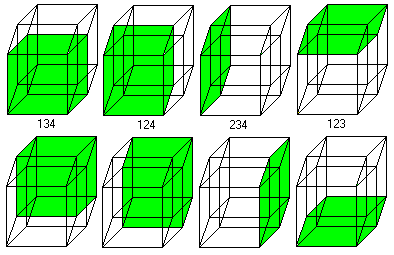So wie der Würfel von 6 Quadraten begrenzt wird,
so bilden 8 Würfel den Hyperkubus. |
Die Zahlen 134, 124, 234, 123 geben Basisvektoren an (unten
erklärt).
Wer den 3D-Blick beherrscht, kann den Hyperkubus auch
dreidimensional betrachten:
Zentralprojektionen
top
.... ... |
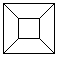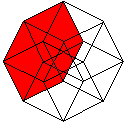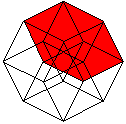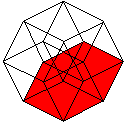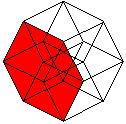
In einer Zentralprojektion ist der Würfel verzerrt.
Von den sechs Quadraten eines Würfels erscheinen vier als Trapeze,
die zwischen dem kleinen und großen Quadrat liegen. |
... |
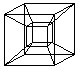Daraus ist eine Darstellung des Hyperkubus entstanden,
die auf
Viktor Schlegel (1888) zurückgeht. |
... ... |
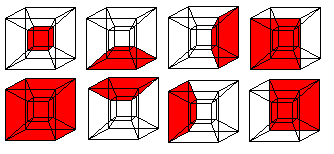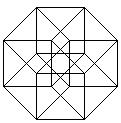
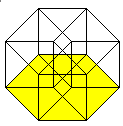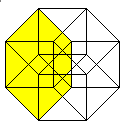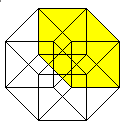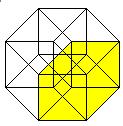
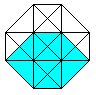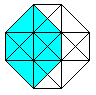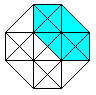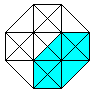
Von den 8 Würfeln erscheinen 6 als Pyramidenstümpfe,
die zwischen einem kleinen und großen Würfel
liegen. |
 |
An jeder Ecke stoßen 4 Würfel, 6 Quadrate und
4 Kanten zusammen.
An jeder Kante stoßen 3 Würfel und 3 Quadrate
zusammen.
An jedem Quadrat stoßen 2 Würfel zusammen.
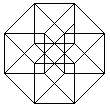
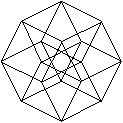
Netze top
... ......... |
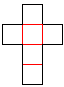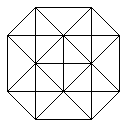
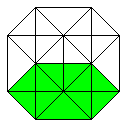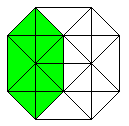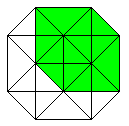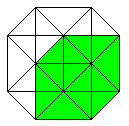
Klappt man den Würfel auf, so entsteht sein Netz.
Die 6 Quadrate haben zusammen 6*4=24 Seiten. 2*5=10 Seiten (rot) sind gebunden.
Beim Zusammenbau des Würfels müssen die restlichen 14 Seiten
paarweise zusammengeklebt werden. Es gibt insgesamt 11 Netze.
|
... ...... |
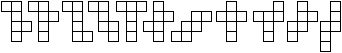
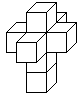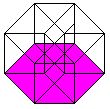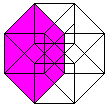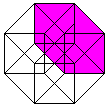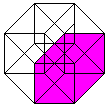
Klappt man den Hyperkubus auf, so entsteht als Netz ein
Würfelkörper aus 8 Würfeln. Die acht Würfel haben zusammen
8*6=48 Quadrate. 2*7=14 Quadrate sind gebunden. Beim Zusammenbau des Hyperkubus
müssen die restlichen 34 Quadrate paarweise zusammengeklebt werden.
Peter Turney bzw. Dan Hoey haben 261 Netze gezählt. |
Schnitte top
... ... |
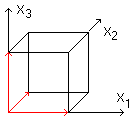Ein Würfel (genauer: Einheitswürfel) wird durch
drei paarweise aufeinander senkrecht stehende Einheitsvektoren (rot) erzeugt.
Sie bilden ein Koordinatensystem (O,x1,x2,x3). Die Eckpunkte lassen sich
dann durch Zahlentripel, gebildet aus den Zahlen 0 und 1, darstellen. |
... ........ |
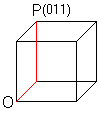Zum Punkt P gehört das Tripel (011). Man gelangt
zu P, indem man vom Nullpunkt (000) aus zuerst in Richtung x2 und dann
in Richtung x3 geht. Das wird festgehalten mit 011. |
... ...... |
Auf diese Weise kann man alle acht Eckpunkte mit Koordinaten
versehen.
Es kommen alle Dreierkombinationen aus 0 und 1 vor. |
... ......... |
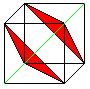Addiert man die Koordinaten eines Punktes, so ergeben
sich die Summen 0,1,2 oder 3. Den Summen 0 und 3 sind gegenüberliegende
Eckpunkte des Würfels zugeordnet. Sie stellen eine Raumdiagonale dar
(grün). Verbindet man die Punkte mit den Summen 1 und 2, so ergeben
sich Dreiecke (rot). |
Setzt man x1+x2+x3 = a und lässt a alle Zahlen von 0
bis 3 durchlaufen, so ergibt sich für jedes a eine Schnittebene. Der
Schnitt erfolgt senkrecht zur Raumdiagonalen von (000) nach (111). Berühmt
ist das Sechseck für a=1,5.
... ... |
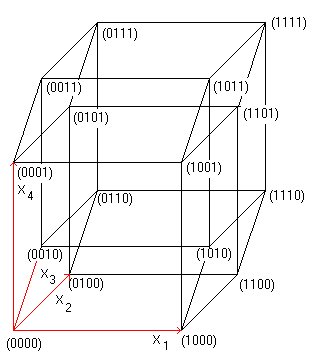Entsprechend erzeugen 4 Basisvektoren (rot) den Hyperkubus.
Als Koordinaten kommen alle Viererkombinationen aus 0
und 1 vor. |
... ...... |
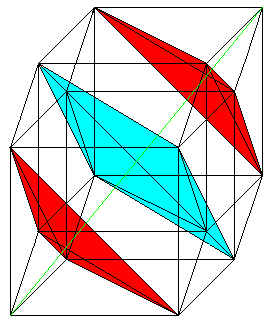Addiert man die Koordinaten eines Punktes, so ergeben
sich die Summen 0,1,2,3 oder 4. Den Summen 0 und 4 sind Eckpunkte zugeordnet.
Sie stellen eine Raumdiagonale dar (grün).
Verbindet man die Punkte mit den Summen 1 und 3, so ergeben
sich zwei Tetraeder (rot). Für die Summe 2 ergibt sich ein Oktaeder
(blau).
Setzt man x1+x2+x3+x4= a und lässt a alle Zahlen
von 0 bis 4 durchlaufen, so ergibt sich für jedes a ein Schnittkörper.
Der Schnitt erfolgt senkrecht zur Raumdiagonalen von (0000) nach (1111). |
Weitere Bilder top
Auch ein Rhombendodekaeder kann einen Hyperkubus darstellen.
Der n-dimensionale
Würfel top
Der Hyperkubus ist ein Gedankengebilde. Man erhält
eine plausible "Erklärung" für seine Eigenschaften durch das
Permanenzprinzip, das in der Mathematik häufig angewandt wird, um
"vom Bekannten zum Unbekannten" zu gelangen.
"Würfel" mit den Dimensionen 1, 2 und 3 haben folgende
Eigenschaften.
Es müssten jetzt in der nächsten Zeile die Daten
des Hyperwürfels folgen. Dimension=4, Ecken=16 ist klar. Wie die Folge
der Kanten und Quadrate fortgesetzt werden muss, beschreibt das folgende
Bildungsgesetz.
Setzt man in die Terme n=4, so erhält man für den
Hyperkubus folgende Daten.
Daten des 5-dimensionalen Würfels, eine Zugabe:
Der Hyperkubus
im Internet top
Englisch
Eric W. Weisstein, (MathWorld)
Hypercube
Peter Turney
Unfolding
the Tesseract
Wikipedia
Hypercube,
Tesseract,
Fourth
dimension, Josephskreuz
Deutsch
Hans Walser
Der
n-dimensionale Hyperwürfel (.pdf-Datei)
Manfred Hörsch
Hyperkubus
- Videos
Roberto Neumann
Hyperwürfel
und Hyperkugeln
Wikipedia
Hyperwürfel,
Tesserakt,
4D,
Joseph
Cross (tower)
Referenzen top
(1) Martin Gardner: Mathematischer Karneval, Frankfurt
am Main, 1975
(2) Fritz Reinhardt, Heinrich Soeder: dtv-Atlas zur Mathematik
I (Seite 172), München 1977
(3) R.Thiele, K.Haase: Der verzauberte Raum, Leipzig,
1991
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2001 Jürgen Köller
top |
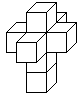