Tangentenviereck
Inhalt dieser Seite
Was ist ein Tangentenviereck?
Formeln
Besondere Tangentenvierecke		 Verschiedenes
Tangentenviereck im Internet 
Referenzen.
Zur Hauptseite    "Mathematische Basteleien"

Was ist ein Tangentenviereck?
... Ein Tangentenviereck ist ein Viereck mit einem Inkreis. 

Die Seiten sind Tangenten. So entsteht der Name. 

Formeln    top
Seiten
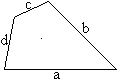... Für die Seiten des Tangentenvierecks gilt a+c=b+d. 

D.h., die Summe der Längen gegenüberliegender Seiten ist gleich. 

Beweis:
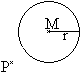...... Dazu geht man von einer Konstruktionsaufgabe aus:
Zeichne von einem Punkt P aus an den Kreis mit dem Mittelpunkt M und dem Radius r die Tangenten. 
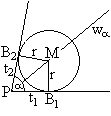...... Es gibt zwei Tangenten, die den Kreis in den Punkten B1 und B2 berühren.
Die Berührradien stehen senkrecht auf den Tangenten. 
Es ist eine achsensymmetrische Figur mit der Gerade PM als Symmetrieachse entstanden.
Damit sind die rechtwinkligen Dreiecke  PB1M und PB2 M kongruent.
Die Tangentenabschnitte t1 und t2 sind gleich. 
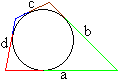...... Auch von den anderen Eckpunkten gehen gleich lange Tangentenabschnitte aus. 
Man kann a+c=b+d ablesen, wzbw. 
Die Umkehrung gilt auch: Gilt in einem Viereck a+c=b+d, so ist es ein Tangentenviereck. 
Beweis:
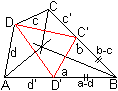...... Es sei ohne Einschränkung der Allgemeinheit a>d und b>c.
Dann trägt man auf a die Strecke d von A aus ab und erhält Punkt D'.
Desgleichen trägt man auf b die Strecke c von C aus ab und erhält Punkt C'. 
Man zeichnet das Dreieck D'C'D (rot). 
Es sind die gleichschenkligen Dreiecke D'DA, D'C'B und DC'C entstanden. 
Die Symmetrieachsen der Dreiecke sind gleichzeitig  Mittelsenkrechten des Dreiecks AB'C'. Sie gehen also durch einen Punkt, der von allen Seiten den gleichen Abstand hat. Das bedeutet aber, das Viereck ABCD ein Tangentenviereck ist.
(2), Seite 14f.
Flächeninhalt
Es gilt die Formel A=sr mit s=(a+b+c+d)/2. r ist der Radius des Inkreises.
Zum Beweis:
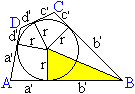...... Zur Herleitung einer Formel werden die Seiten a bis d durch die Tangentenabschnitte a' bis d' ausgedrückt. 
Das Viereck setzt sich nämlich paarweise aus acht rechtwinkligen Dreiecken mit den Katheten a' bis d' zusammen. 
Es gilt: A = 2a'r/2+2b'r/2+2c'r/2+2d'r/2 = (a'+b'+c'+d')r=(a+b+c+d)/2*r. 
 Setzt man s=(a+b+c+d)/2, so ist A=sr.
Beachtet man noch a+c=b+d, so gilt auch A=(a+c)r=(b+d)r
Noch eine Formel 
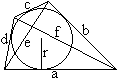
Es gibt eine Beziehung zwischen den Seiten, den Diagonalen und dem Radius des Inkreises. 

r=sqrt[4e²f²-(a²-b²+c²-d²)²]/[2(a+b+c+d)]

Besondere Tangentenvierecke      top
Tangentenvierecke unter den Standard-Vierecken
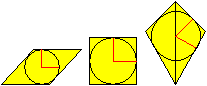
...... Es sind die Raute, als ihr Sonderfall das Quadrat, und das Drachenviereck.

Trapez
Es gibt Trapeze, die auch Tangentenvierecke sind. 
...... Dazu zeichnet man an einen Kreis zwei horizontal liegende Parallelen. 
Zwei weitere Tangenten rechts und links an den Kreis ergänzen die Figur zum Tangentenviereck.
Tangentenviereck um ein Sehnenviereck
Gibt man ein Sehnenviereck vor, so kann man dazu ein Tangentenviereck finden. 
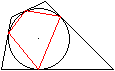...... Man zeichnet in den Berührpunkten die Tangenten. 
Gibt man ein Tangentenviereck vor, so kann man umgekehrt dazu ein Sehnenviereck finden. Man verbindet die Berührpunkte. 
Sehnentangentenviereck
Es ist schon etwas Besonderes, wenn ein Viereck sowohl ein Tangentenviereck als auch ein Sehnenviereck ist. 
Ein Beispiel ist das Quadrat.
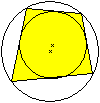...... Das nebenstehende Viereck hat sowohl einen In- als auch einen Umkreis. 
Vierecke dieser Art heißen Sehnentangentenvierecke. 

Hier fallen die Mittelpunkte der Kreise nicht wie z.B. beim Quadrat zusammen. 
Für das Sehnentangentenviereck vereinfachen sich die Formeln. 
Für ein Sehnenviereck gilt A=sqrt[(s-a)(s-b)(s-c)(s-d)] mit s=(a+b+c+d)/2.
Für ein Tangentenviereck gilt a+b=c+d
Dann ist s=a+c=b+d. Das führt zur einfachen Formel A=sqrt[abcd] 
Für ein Sehnenviereck gilt für den Radius des Umkreises R=sqrt{[(ac+bd)(ad+bc)(ab+cd)]/[(s-a)(s-b)(s-c)(s-d)]}/4
Die Formel A=sqrt[abcd] führt zu R=sqrt[(ac+bd)(ad+bc)(ab+cd)]/abcd]}/4
Für ein Tangentenviereck gilt A=sr.
Daraus folgt mit A=sqrt[abcd] die Formel für den Radius des Inkreises r=sqrt[abcd]/s
Ist x die Entfernung der Mittelpunkte von Um- und Inkreis, so gilt die Formel 1/(R+x)²+1/(R-x)²=1/r².

Verschiedenes     top
Zwei Schnittpunkte
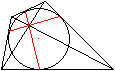...... Verbindet man die Berührungspunkte zweier gegenüberliegender Seiten, so fällt der Schnittpunkt ihrer  Verbindungslinien mit dem Schnittpunkt der Diagonalen zusammen. 

Gerade im Tangentenviereck
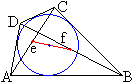...... Verbindet man die Mittelpunkte der Diagonalen, so liegt der Mittelpunkt des Inkreises auf der Verbindungslinie. 
Einen Beweis findet man bei Antonio Gutierrez unter dem Stichwort Newton's Theorem (URL unten)
Bitte den Lautsprecher einschalten :-).
Viereck aus den Winkelhalbierenden
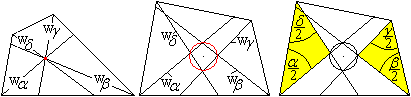...... Der Mittelpunkt des Inkreises eines Tangentenvierecks ist der Schnittpunkt der Winkelhalbierenden. 
Zeichnet man in ein beliebiges Viereck die Winkelhalbierenden ein, so entsteht im Allgemeinen ein  Sehnenviereck. 
Beweis:
Es ist zu zeigen, dass zwei Gegenwinkel des Vierecks die Summe 180° haben. 
Dazu betrachtet man zuerst die gelben Dreiecke. Der dritte Winkel ist 180°-alpha/2-delta/2 bzw. 180°-beta/2-gamma/2. Diese Winkel sind die Scheitelwinkel zweier gegenüberliegenden Winkel des Vierecks in der Mitte. Addiert man sie, erhält man 360°-(alpha+beta+gamma+delta)/2=180°, wzbw..

Tangentenviereck im Internet      top

Deutsch

Eckard Specht (math4U) 
Tangentenviereck   (7 Aufgaben mit Lösungen), Sehnenviereck   (8 Aufgaben mit Lösungen)
Sehnentangentenviereck   (1 Aufgabe mit Lösung)

Sarah Schultze & Jakob Priwitzer ( Ausarbeitung zu einer Geometrie-Vorlesung an der Universität Bremen)
Das Sehnen- & Tangentenviereck (.pdf-Datei) 

Universität Bayreuth Lehrstuhl für Mathematik und ihre Didaktik
Konstruktion eines Tangentenvierecks,  Sehnen-Tangenten-Viereck, 
Symmetrisches Trapez als Sehnen-Tangenten-Viereck  (Geonet)

Wikipedia
Tangentenviereck, Satz von Pitot, Sehnenviereck


Englisch

Eric.W.Weisstein
Tangential Quadrilateral,  Bicentric Quadrilateral, Cyclic Quadrilateral,  Cyclic Polygon, 

Wikipedia
Tangential Quadrilateral, Pitot theorem,  Cyclic quadrilateral

Referenzen   top
(1) Hahn/Dzewas: Mathematik 8.Schuljahr, Braunschweig 1990 [ISBN 3-14-112958-4] 
(2) W.Lietzmann: Altes und Neues vom Kreis, Leipzig und Berlin 1935
(3) Theo Kühlein: Ebene Trigonometrie II, Mentor-Repetitionen, Berlin 1962 (7th ed.1974)  [ISBN 3-580-63140-3]

Die Seite enthält Tipps von Torsten Sillke.
 Feedback: Emailadresse auf meiner Hauptseite

URL meiner Homepage:
https://www.mathematische-basteleien.de/

©  2006 Jürgen Köller

top
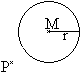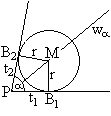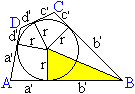