|
What is a Spirograph?
...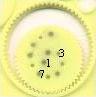 ... ... |
The Spirograph is a mathematical toy, which you can use
for drawing nice figures.
In the simplest case it exists of a fixed circle, used
as a template, and a smaller rolling circle with holes. |
Drawing a figure:
Hold the template (clipping). Stick a ballpoint pen through
one of the holes of the smaller circle. Roll it inside the bigger fixed
circle. Draw it on a sheet of paper. Cogs at the edges of the circles guarantee
a reliable unrolling and prevent sliding.
It is a pity that the spirograph introduced here is non-transparent.
It was a gift of my savings bank at the "World Saving Day", if I remember
correctly.
Drawing Exercises top
...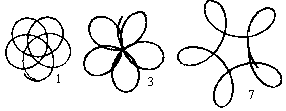 ... ... |
You can draw rosettes with five points easily.
I chose only three of twelve possible holes. They are
representative for the possible shapes. |
If you look at the figures more accurately, you see
that they aren't closed after five revolutions. This is intended:
...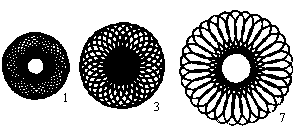 ... ... |
If you go on drawing you'll get some nicely shaped rosettes.
This shows the attraction of spirograph figures. |
Formulas top
You can find parameter formulas for the figures, which
describe them mathematically.
Names:
...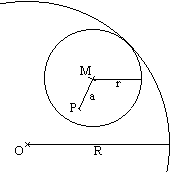 ... ... |
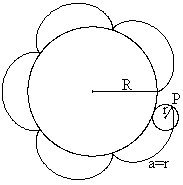
The large circle (radius R) is given and fixed. The small
circle (radius r) rolls on its inner side. There is point P fixed on the
inner circle.
It has the distance a from the centre M of the small
circle.
Now you follow the way of point P during rolling. |
Calculations:
... ... ... |
In the end you have to use both trigonometric formulas. |
Result:
...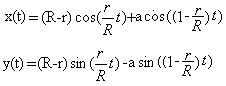 ... ... |
You get the parametric equations for the movement of
the point on the left.
The coordinates x and y of point P depend on the angle
t.
The variables R, r and a are constant.
|
The trigonometric formulas guarantee periodical movements.
The variables (R - r) and a determine the height, the ratio (r : R) the
periodicity of the drawings.
Hypocycloids top
If you use a program to draw the
graph of the equations, you get the so-called hypocycloids.
...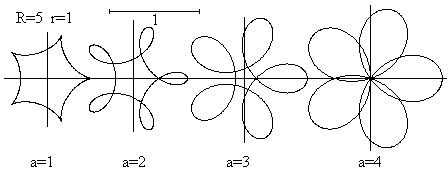 ... ... |
The parameter a is different for each picture.
You also can choose cases, which cannot be drawn with
the spirograph, because the point P lies outside the rolling circle. |
There are closed curves in difference to the spirograph drawings,
because the ratio (R : r) is a digit. It is sufficient to choose the numbers
0 to 5*2Pi for t.
The ratio (R : r) is not a digit, so that you get the
graphs from above.
...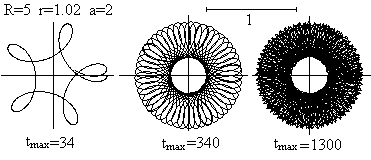 ... ... |
The shape of a rosette also depends on the number of
revolutions. |
Epicycloids top
... ... ... |
You get another kind of cycloids, if you let unroll the
smaller circle (r=1) outside the fixed circle(R=5). This is also
realized at the spirograph with two circles.
Parameter equations:
|
If you transfer the equations to graphs
with the help of a program, you get so-called epicycloids.
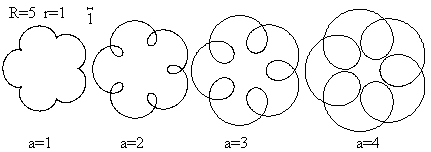 ... ... |
The parameter a is changed.
You also can choose cases, where the point P lies outside
the rolling circle. |
Cycloids top
 |
If you roll the circle on a straight line, a fixed point
on the circle line describes the cycloid. |
The standard equations of the cycloid are x = r[t sin(t)
] and y = r[1 cos(t) ], where r is the radius of the rolling circle and
t goes through the numbers from 0 to 2Pi for one period.
It is remarkable that the length of a cycloid is eight
times as long as the radius of the producing circle. The surface between
x axis and cycloid is three times as big as the surface of the producing
circle.
You get more cycloids if the point P writing the cycloid
is within or outside the rolling circle.
In the first case a shortened cycloid develops, in the
second case an extended one.
The general parametric representation is x = rt-a sin(t)
und y =r-acos(t). R is the radius of the rolling circle and a the
distance of the point P of its center.
...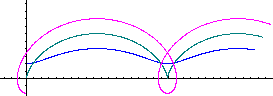 ... ... |
There are r=3 and a=1 (blue), a=3 (green) and a=5 (red).
the variable t follows 0<t<10. |
A rectangle and two half circles sitting on two opposite
sides belong to this part of the spirograph. The drawing is a combined
epicycles / cycloids.
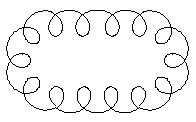 |
A program found parts of the graph on the left with the
help of the following parametric equations
Epicycloids equations on the left, cycloids equations
on the right.
|
Repeating Figures top
There is a stencil with simple figures inside and a fixed
circle, which also belongs to the spirograph system.
... ... ... |
...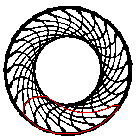 ... ... |
You draw a figure, move the wheel further by one cog
and draw the next figure.
You repeat this procedure as long as cogs are there.
In the end there is a ring for instance. |
These drawings aren't interesting from a mathematical view,
but very effective.
You can read more on my German
page Epizykloide.
Spirograph
on the Internet
top
English
Nathan Friend
inspirograph
(Applet)
Richard Parris (Freeware-Programs)
winplot
Wikipedia
Spirograph,
Harmonograph
German
Jutta Gut
Zykloiden
Wikipedia
Spirograph
(Spielzeug), Zykloide,
Epizykloiden
References top
W.Leupold...: Analysis für Ingenieur- und Fachschulen,
Verlag Harri Deutsch, Frankfurt/M.
Feedback: Email
address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
2000 Jürgen Köller
top |
 ...
...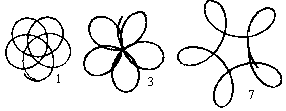 ...
... ...
... ...
...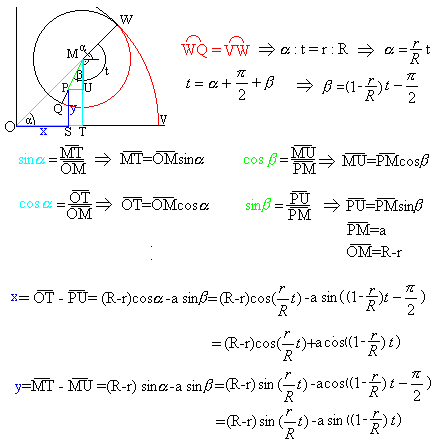
 ...
...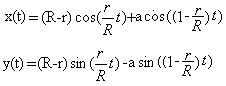 ...
...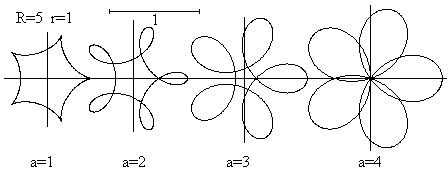 ...
... ...
... ...
...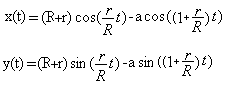
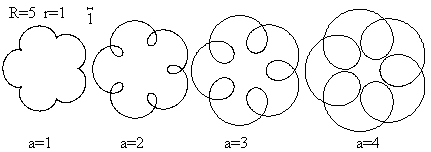 ...
...
 ...
...
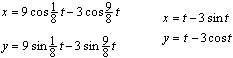
 ...
... ...
...