|
Was ist das Körbchen?
... ... ... |
Das Körbchen ist ein quaderförmiger Behälter,
den man aus einem quadratischen Stück Papier faltet. |
Falten des Körbchens
top
1
...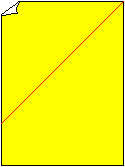 .... .... |
Falte ein Blatt Papier vom Format DIN A 4 an der roten
Linie.
 |
2
...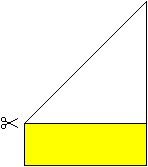 |
Schneide den unteren Streifen ab.
 |
3
... |
Es ist ein Quadrat entstanden.
 |
4
...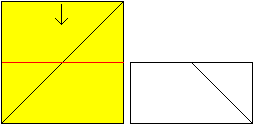 |
Falte an der roten Linie von oben nach unten.
Es entsteht ein Rechteck. |
5
...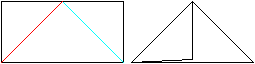 |
Falte an der roten Linie nach vorne und an der blauen
Linie nach hinten.
Es entsteht ein Dreieck.

|
6
...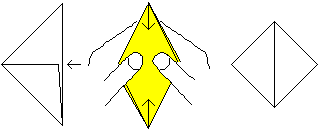 ... ... |
Drehe das Dreieck und greife in Pfeilrichtung mit beiden
Daumen in das Dreieck und lege die beiden Ecken oben und unten aufeinander.
Es entsteht ein Quadrat. |
7
...
|
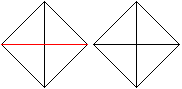
Falte das obere Blatt an der roten Linie nach oben und
mache die Faltung wieder rückgängig.
Die Mitte des Quadrats ist markiert.
 |
8
...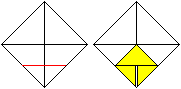 |
Falte an der roten Linie noch oben.
 |
9
...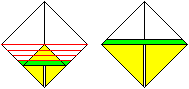 ... ... |
Rolle einen Streifen (grün markiert) nach oben hin,
drücke die Rolle platt, wenn sie das obere Dreieck erreicht hat. (Wenn
man noch keine Übung hat, sollte man die roten Linien durch mehrfaches
Halbieren vorfalten.
 |
10
...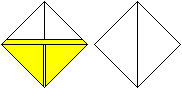 ... ... |
Drehe das Papier um.
Es kommt eine freie Fläche in Form eines Quadrates
zum Vorschein.
 |
11
...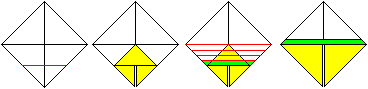 |
Wiederhole die Schritte 8 und 9. |
12
...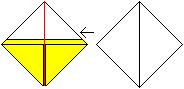 |
Klappe die obere rechte Lage an der roten Linie nach
links.
Es entsteht wieder eine freie Fläche in Form eines
Quadrates.
 |
13
...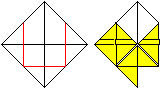 |
Falte dreimal nacheinander an den roten Linien. In der
Mitte treffen sich drei Dreiecke.
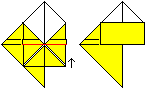
 |
14
...
|
Decke den Treffpunkt der drei Dreiecke zu. Falte dazu
ein Rechteck an der roten Linie nach oben.
 |
15
...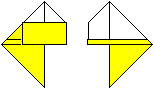 |
Drehe das Papiergebilde um.
 |
16
...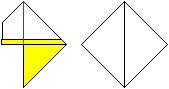 |
Klappe wieder die obere rechte Lage an der roten Linie
nach links.
Es entsteht wieder eine freie Fläche in Form eines
Quadrates.
 |
17
...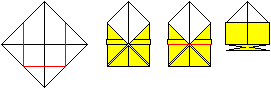 ... ... |
Falte wieder dreimal an den roten Linien. In der Mitte
treffen sich drei Dreiecke. Decke den Treffpunkt der drei Dreiecke zu.
Falte dazu ein Rechteck an der roten Linie nach oben. |
18
...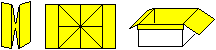 ... ... |
Drehe das fast fertige Körbchen um, öffne es
und forme es zu einem Kasten.
 |
19
Aus dem Kasten wird ein Körbchen, wenn man noch
für einen Henkel sorgt.
...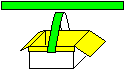 ... ... |
Den Henkel schneidet man aus dem Streifen aus Schritt
2 dieser Anleitung zurecht. Am besten nimmt man zwei Lagen.
Befestige die beiden Enden des Streifens. Schiebe sie
seitlich unter die Rolle aus Schritten 9 und 11. Man kann die Wicklungen
an den Stellen vorübergehend vorsichtig entrollen.
 |
Es ist eleganter, den Streifen schon
in den Schritten 9 und 11 mit einzurollen. Aber ich befestige den
Henkel erst zum Schluss, da er "unterwegs" stört.
Etwas Mathematik top
...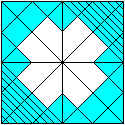 ... ... |
Entfaltet man das Körbchen, so erhält man ein
Quadrat mit dem nebenstehenden Muster. Es ist hier so gefärbt, dass
man das Innere des Körbchens in Weiß erkennt.
Das Körbchen ist ein halber Würfel.
Ist a die Seitenlänge des Quadrates, so hat der Würfel
die Kantenlänge sqrt(2)/4*a. Das ist etwa 0,35*a.
 |
Weitere Behälter
top
Das Körbchen
im Internet top
Deutsch
Das Bastelparadies
Körbchen
basteln
Kikisweb
Körbchen
aus Streifen
Zzzebra
Körbchen
aus Papier
Englisch
Craftideas.info
How
to Craft a Paper Origami Easter Basket
The Jamboree
Paper-woven
Basket
Youtube
How
to Make Easy Paper Basket for Gifts
Referenzen top
Joachim Schönherr: Wir falten und falzen, Leipzig
1990
Therese Mielhaht: Origami - Spaß mit Papierfalten,
Köln 1990
Kommentar top
Das Körbchen gehört wie das Papierschiffchen,
die
Taube, Pfeffer und Salz, das
Portmonee, der Papierbecher und die
Zaubertüte zu den Klassikern des Papierfaltens.
In allen Fällen geht man von einem Rechteck aus und
faltet Figuren ohne einzuschneiden oder zu kleben. Das ist Origami in seiner
ursprünglichen Form.
Das Körbchen war in meiner Kindheit, später
bei meinen Kindern und ist heute bei meinen Enkelkindern ein Favorit :-).
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2003 Jürgen Köller
top |
 ...
... ....
....



 ...
...

 ...
... ...
...





 ...
... ...
... ...
... ...
...
