Was ist der Kehrwert?
Kehrwert einer Dezimalzahl
Nenner rational machen Zu erwähnen sind noch die Kehrwerte von Wurzeln. Zum Beispiel ist es üblich, den Kehrwert einer Zahl wie sqrt(2), nämlich 1/sqrt(2), nicht stehen zu lassen, sondern die Wurzel im Nenner zu beseitigen. Das erreicht man durch Erweitern des Bruches mit sqrt(2). Dann ist 1/sqrt(2) =sqrt(2)/2. Dadurch wird die Zahl anschaulicher, und man gelangt so zu der üblichen Darstellung einer irrationalen Zahl.. Man nennt diese Rechnung "Rationalmachen des Nenners". Gegenzahl Der Kehrwert heißt im Englischen "Multiplicative inverse". Es gibt auch den Begriff "Additive inverse", und das ist im Deutschen die Gegenzahl. So wie für die Multiplikation x*(1/x) = 1 gilt, so für die Addition x+(-x) = 0. Die Zahl -x ist die Gegenzahl. Die Null spielt für die Addition die gleiche Rolle wie die Eins bei der Multiplikation. In beiden Fällen sind die Eins bzw. Null "neutrale Elemente". Verknüpft man sie mit einer beliebigen reellen Zahl, so ändern sie die Zahl nicht: x*1 = x und x+0 = x. Graphische Darstellungen top
Ableitungen
Stammfunktion
Kehrwert
von Funktionstermen top
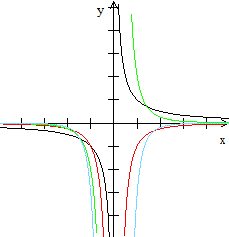
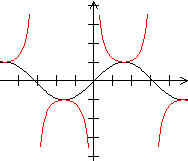
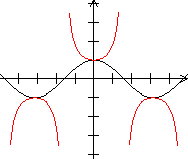
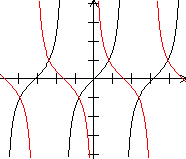
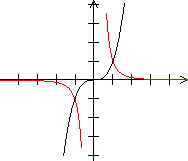
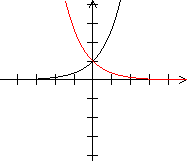
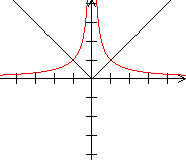
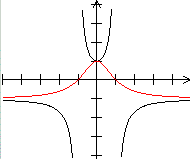
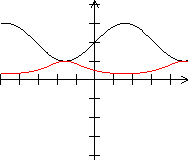
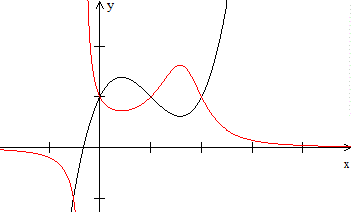
Umkehrfunktion Es gibt zu einer Funktion neben der reziproken Funktion auch die Umkehrfunktion. Das ist eine Funktion, bei der jedem y-Wert ein x-Wert eindeutig zugeordnet wird. Bei der Funktion gehört zu jedem x-Wert genau ein y-Wert. Die Umkehrfunktion kann leicht mit der reziproken Funktion verwechselt werden, nicht nur wegen des ähnlichen Namens, sondern auch wegen der Schreibweise des Funktionsterms. Man schreibt 1/f(x) besser nicht als f-1(x). Der Term f-1 beschreibt nämlich die Umkehrfunktion von f. Für f-1(x) sollte man deshalb, wenn überhaupt, [f(x)]-1 schreiben. Reziproke Funktion Es folgt eine Reihe von Graphen der Funktion und der reziproken Funktion.
Das sind Sinus und Kosekans, Kosinus und Sekans, Tangens und Kotangens.
Begründungen Die Aussagen (1), (2) und (3) sind einfach einzusehen. Zum Nachweis der Aussagen (4) und (4') muss man etwas rechnen. Es gilt nach der Kettenregel r' = (1/f)' = (f-1)' = -(f-2)f ' =-f '/f² und nach der Quotientenregel r'' = -(f ''f²-2f f '²)/f4= (-f ''f+2f '²)/f³. Gelten an der Stelle x2
die Aussagen f '(x) = 0 und f ''(x)>0, so ist dort ein Minimum.
(4') Ist an der Stelle x3 ein Maximum, so nimmt r(x) dort ein Minimum an. Der Beweis verläuft analog. Summe
von Kehrwerten top
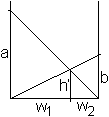
Sich kreuzende Strecken
Es sei w1+w2=w. Nach dem Strahlensatz gilt rechts w2:w=h':b oder w2=h'w/b und links w1:w=h':a oder w1=h'w/a. Daraus folgt mit w1+w2=w die Gleichung w=h'w/b+h'w/a oder 1=h'(1/b+1/a) oder h'=ab/(a+b) = (1/2)h, wzbw.. Die Figur stellt auch die bekannte Leiter-Aufgabe von den sich kreuzenden Leitern dar. Siebeneck
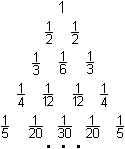
Harmonisches Dreieck
Reihen
aus Kehrwerten
Die Kehrwerte der natürlichen Zahlen heißen in der Bruchrechnung Stammbrüche. Die harmonische Reihe geht aus der harmonische Folge hervor. Sie ist die Folge der Partialsummen der harmonischen Folge. Alternierende harmonische Reihe Die alternierende harmonische Reihe geht aus der harmonischen Reihe hervor. Das Vorzeichen der Summanden wechselt sukzessive. Leibniz-Reihe In der alternierenden harmonischen Reihe setzt man an Stelle der natürlichen Zahlen die ungeraden Zahlen. Reihe mit den Kehrwerten der Quadratzahlen In der harmonischen Reihe setzt man an Stelle der natürlichen Zahlen Quadratzahlen. Kempner-Reihen Die Kempner-Reihen gehen aus der harmonischen Reihe hervor. Man entfernt alle Zahlen, die im Nenner die Ziffer 1 enthalten. Aus der Reihe 1+1/2+1/3+1/4+1/5+1/6+1/7+1/8,+1/9+1/10+1/11... wird dann 1+1/2+1/3+1/4+1/5+1/6+1/7+1/8,+1/9+1/20+1/22+... Wegen der 10 Ziffern gibt es 10 Kempner-Reihen. Das Besondere ist, dass alle Kempner-Reihen konvergent sind. Gefunden bei http://mathworld.wolfram.com (URL unten). Kehrwerte
bei Größen top
Kehrwert einer Größe Schwingungsdauer und Frequenz Eine kennzeichnende Größe der Schwingung ist die Schwingungsdauer T. Ebenso ist der Kehrwert, die Frequenz f, in Gebrauch. Beide Größen sind durch die Gleichung T*f=1 oder f = 1/T miteinander verknüpft. Es ist für die Anschauung sinnvoll, für langsame Schwingungen die Schwingungsdauer zu verwenden. > Ein Fadenpendel der Länge 1m hat z.B. die Schwingungsdauer T = 0,68 s. > Eine Stimmgabel mit der Schwingungsdauer T= 0.00227272727 s kennzeichnet man besser mit dem Kehrwert, nämlich f=440 1/s = 440 Hz. Mir sind noch zwei weitere Größenpaare geläufig, nämlich der elektrische Widerstand R und der elektrische Leitwert G = 1/R bzw. bei Brillen die Brennweite f und die Brechkraft D=1/f, gemessen in Dioptrien. Proportionale Größen Zwei Größen A und B sind proportional, wenn ihr Quotient A/B konstant ist. Es gibt Beispiele, da hat auch der Kehrwert des Proportionalitätsfaktors eine Bedeutung. Benzinverbrauch Die von einem Auto zurückgelegte Strecke und die dabei verbrauchte Benzinmenge sind im Mittel proportional. Der Proportionalitätsfaktor ist der Benzinverbrauch. Es ist bei uns üblich, den Benzinverbrauch eines Autos z.B. mit 8,5 l anzugeben. Genauer ist das der Quotient 8,5 l / 100 km. Damit ist gemeint, dass das Auto im Mittel für 100 km die Menge 8,5 l Benzin verbraucht. In Großbritannien oder in den USA wird der Benzinverbrauch durch den Kehrwert angegeben. Man gibt den Weg in Meilen an, den man mit einem Gallon fahren kann. Für einen Vergleich mit 8,5 l / 100 km muss man wissen, dass 1km = 0,6214 miles und 1 gallon = 3,7854 Liter oder 1 Liter = 0,2642 gallons ist. Dann gilt für den Kehrwert (100 km)/ (8,5 l) = (100*0,6214 miles )/(8,5*0.2642 gallons) = (27 miles)/(1 gallon) = 27 mpg. Um die Konfusion noch zu steigern: In Großbritannien wird der Benzinverbrauch zwar auch in der Einheit mpg angegeben, allerdings gilt nicht 1 gallon = 3,7854 Liter, sondern 1 gallon = 4,546 Liter. Einem Benzinverbrauch von 8,5 l entspräche dann der größere Wert 32,10 mpg. Im Englischen ist der Name Benzinverbrauch
eigentlich falsch, da er ja der Kehrwert des Benzinverbrauchs ist. Man
spricht auch von mileage und d.h. Fahrleistung oder Laufzeit.
Umrechnungskurs Man kann den Umrechnungskurs zwischen den Währungen Euro und britisches Pfund auf zweierlei Weise angeben, Geschwindigkeit Die Geschwindigkeit v kennzeichnet eine gleichförmige Bewegung. Sie ist der Proportionalitätsfaktor v=s/t zur Proportionalität s ~ t. Dabei sind s der zurückgelegte Weg und t die verstrichene Zeit. Grundsätzlich kann jeder Kehrwert eines Proportionalitätsfaktors gebildet werden. Die Frage ist nur, ob er sinnvoll ist und ob er "im täglichen Leben" auch benutzt wird. Dazu ein Beispiel. Bildet man den Kehrwert t/s, so ist er
ein Maß für die "Langsamkeit", denn bei einem konstantem Weg
ist der Quotient um so größer, je mehr Zeit verstreicht. - Man
könnte vielleicht die Bewegung einer Schnecke durch t/s ausdrücken,
zum Beispiel durch die Zeit, die sie für einen Meter braucht. Jedoch
fand ich z.B. auf der entsprechenden Wikipedia-Seite eine Geschwindigkeitsangabe:
Die Schnecke bewegt sich im Mittel mit 7cm / min im "Schneckentempo" fort.
Durch Wahl geeigneter Einheiten ist die Maßzahl einstellig und somit
anschaulich.
Ich stellte fest, dass Amerikaner, wenn sie mit dem Auto über größere Strecken fahren, die Entfernungen meist in Stunden angeben, auch weil es auf den Highways Geschwindigkeitsbegrenzungen gibt. Das ist für sie treffender als Meilen. - Wir Deutsche bevorzugen Kilometerangaben. Stunden geben wir nur an, wenn wir demonstrieren wollen, wie schnell wir wieder einmal waren oder wie lange wir im Stau standen. Antiproportionale Größen Zwei Größen A und B sind antiproportional, wenn ihr Produkt AB konstant ist. Der Graph ist eine rechtwinklige Hyperbel. Da ist eine Analogie zu Zahl und Kehrzahl. Bei ihnen ist das Produkt 1, und der Graph ist die spezielle Hyperbel f(x) = 1/x. Summe von Kehrwerten In der Schulphysik kommen Gleichungen mit Summen von Kehrwerten von Größen vor. Es folgt eine Auswahl. Ersatzwiderstand parallel geschalteter Widerstände
Ersatz-Kapazität hintereinander geschalteter Kondensatoren
Ersatz-Induktivität parallel geschalteter Spulen
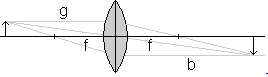
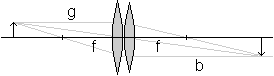
Linsenformel
Linsensystem
Kehrwert im Internet top Deutsch mathekram [at]
Wikipedia
Englisch Eric W. Weisstein (MathWorld)
Wikipedia
URL meiner Homepage:
© Oktober 2014 Jürgen Köller |
 ...
...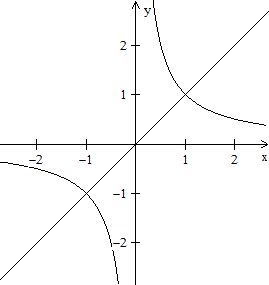 ...
...
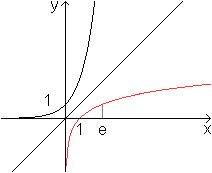 ...
...

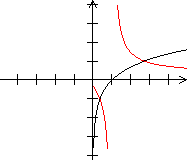



 ...
... ...
... ...
... ...
... ..
..