|
Was ist ein regelmäßiges Siebeneck?
|
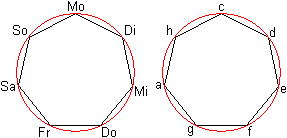
Das regelmäßige Siebeneck ist ein Vieleck mit
sieben Ecken
sieben gleich langen Seiten und
sieben gleich großen Innenwinkeln. |
Das regelmäßige Siebeneck heißt auch Heptagon oder manchmal
Septagon, auf dieser Seite meist einfach Siebeneck.
Größen des Siebenecks
top
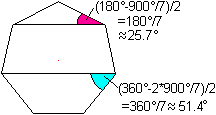
Winkel im Siebeneck
Weitere Größen
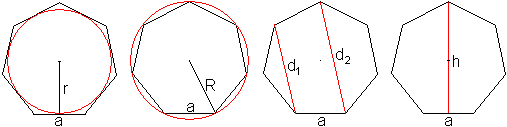
Ist die Seite a gegeben, so lassen sich daraus der Radius r
des Inkreises, der Radius
R des Umkreises, die Diagonalen
d1
und
d2
und die Höhe h, der Flächeninhalt
A
und der Umfang U errechnen.
Vorbemerkung
... ... |
In Formelsammlungen fehlt das Siebeneck. 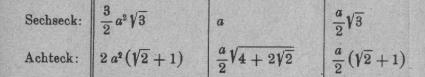Das liegt daran, dass man
seine Größen nicht wie zum Beispiel beim Sechs- und Achteck
durch Wurzelterme ausdrücken kann. |
Formeln
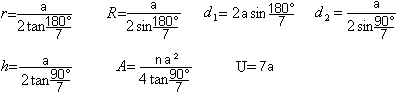
Herleitung der Formeln
Radius r des Inkreises und Radius
R
des Umkreises
|
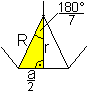
Es gilt sin(180°/7)=(a/2)/R und tan(180°/7)=a/(2r).
Daraus folgen die Formeln R=a/[2*sin(180°/7)] und r=a/[2*tan(180°/7)]. |
Erste Diagonale
|
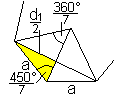
Es gilt sin(90°-180°/7)=cos(180°/7)=d1/(2a).
Daraus folgt d1=2a*sin(180°/7). |
Zweite Diagonale
und Höhe
|
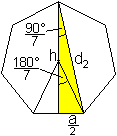
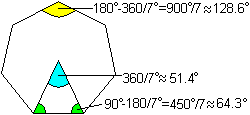
Wegen des Mittelpunktsatzes ist der Umfangswinkel halb so groß
wie der Mittelpunktwinkel.
Diese Aussage ist auf den Umkreis bezogen.
Es gilt tan(90°/7)=(a/2)/h. Daraus folgt h=a/[2*tan(90°/7)].
Es gilt weiter sin(90°/7)=(a/2)/d2. Daraus folgt d2=a/[2*sin(90°/7)]. |
Flächeninhalt
und Umfang
Der Flächeninhalt ergibt sich aus dem 7-fachen der Fläche
des Bestimmungsdreiecks: A=7(a*r/2)=7a²/[4*tan(180°/7)].
Der Umfang ist 7a.
Diagonalen top
Das Siebeneck hat 14 Diagonalen.
... ... |
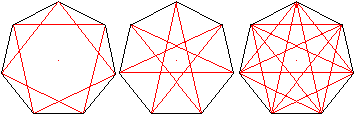Sieben Diagonalen verbinden jeden zweiten und sieben jeden dritten
Eckpunkt.
Die Diagonalen bilden zwei voneinander unabhängige Sterne (Heptagramme).
Sie können in einem Streckenzug gezeichnet werden. |
Die Winkel an den Spitzen der Heptagramme sind 540°/7 und 180°/7.
Zeichnen eines Siebenecks
top
Nicht konstruierbar
Nach Gauss (1796) sind die und nur die p-Ecke (p ist eine ungerade
Primzahl) konstruierbar, bei denen es natürliche Zahlen k gibt, so
dass p=2^(2k )+1 Primzahlen sind.
Das sind p=3, p=5, p=17, ... für k=0,1,2,... Darunter ist
also nicht p=7.
Weitergehende Untersuchungen gehen von der Gleichung z7=1
bezogen auf komplexe Zahlen aus. Näheres findet man bei Robert Geretschläger
(siehe unten).
Zeichnung
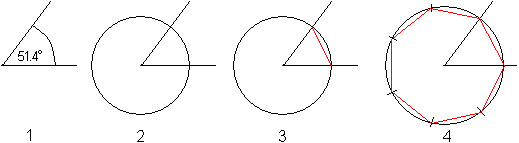(1) Zeichne einen Winkel von 51,4° mit einem Geodreieck.
(2) Zeichne einen Kreis um den Scheitelpunkt.
(3) Zeichne die Sehne.
(4) Trage sie sechsmal auf dem Kreisbogen ab. Zeichne alle Sehnen.
Es ist ein Siebeneck entstanden.
Erste Näherungskonstruktion
Wenn man das Siebeneck nicht exakt mit Zirkel und Lineal konstruieren
kann, so gibt es doch eine Reihe von Näherungskonstruktionen. Es folgen
zwei Beispiele.
... ... |
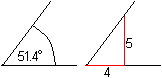Die Zeichnung oben setzt einen Winkel von 51,4° voraus, dann folgen
Konstruktionen.
Diesen Winkel kann man näherungsweise konstruieren.
Man geht von einem (Scheitel-)Punkt 4 Einheiten nach rechts und 5 Einheiten
nach oben. Das dazugehörige Dreieck enthält einen Winkel
von fast 360/7° oder gerundet 51,43°. |
Die Gleichung tan(alpha)=5/4 führt zu einen Winkel von 51,34°.
Dieser Winkel ist nur um 0,17% kleiner als 360/7° .
Man kann tan(alpha) beliebig nahe kommen,
wenn man den Kettenbruch tan(2pi/7) = [1,3,1,15,31,1,3,...] wählt.
Die ersten Näherungsbrüche sind 1, 4/3, 5/4, 79/63, 2454/1957,
2533/2020, 10053/8017, ...
Zweite Näherungskonstruktion
... ... |
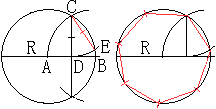>Zeichne einen Kreis um Punkt A mit dem Radius AB=R.
>Zeichne den Kreis um B mit dem Radius AB=R. Du erhältst Punkt
C.
>Zeichne die Höhe CD.
>Zeichne um C einen Kreis mit dem Radius CD. Du erhältst Punkt
E.
>Die Strecke CE ist angenähert die Seite eines Siebenecks. |
Man wählt also die Höhe eines gleichseitigen Dreiecks als Seitenlänge
des Siebenecks.
Überprüfung
... ... |
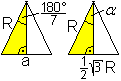Die Höhe in einem gleichseitigen Dreieck ABC oben ist CD=(1/2)sqrt(3)R.
Diese Strecke wird zur Grundseite im Grunddreieck des angenäherten
Siebenecks.
Für den halben Grundwinkel gilt sin(alpha/2)=(1/4)sqrt(3) oder
alpha/2=25,6589°.
Zum Vergleich ist 180/7°=25,7143°. Der Fehler ist 0,22%. |
Zu dieser Konstruktion gibt es auf der
Webseite http://de.wikipedia.org/wiki/Siebeneck eine Animation.
Dort steht auch, dass sich die Konstruktion schon bei Abu l-Wafa (10.
Jahrhundert) findet.
Es gibt im Internet eine zweite Quelle, nämlich eine Faksimile-Ausgabe
in der Sammlung Geometria [Matthäus Roriczer (15.Jahrhundert)] auf
der Webseite der Hochschule Augsburg (URL unten).
Die Hinweise auf diese Näherungskonstruktion und auf die Quellen
stammen von Lutz Führer.
Dreieck im Siebeneck top
... ... |
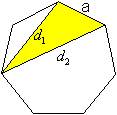Die lange Diagonale, die kurze Diagonale und die Seite des Siebenecks
bilden ein Dreieck. Zwischen den Seiten gelten folgende Beziehungen:
(I) d1²=ad2+a²
(II) d2²=d1d2+a²
(III) d2²=ad1+d1²
|
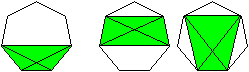
Beweis:
... ...
|
Im Siebeneck treten drei verschiedene gleichschenklige Trapeze mit
einem Umkreis auf.
Aus dem Satz des Ptolemäus ergeben sich die drei Formeln unmittelbar.
Der Satz wird auf meiner Seite Sehnenviereck
bewiesen und besprochen. |
Hier ist eine weitere Formel, die sich
aus dem Satz des Ptolemäus ergibt.
|
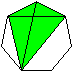
Dazu zeichnet man das nebenstehende grüne Sehnenviereck ein.
Es gilt: d1d2=ad1+ad2 .
Daraus folgt a=(d1d2)/(d1+d2).
Die Seite ist das halbe harmonische Mittel der beiden Diagonalen. |
Es gibt noch viele weitere interessante
Aussagen zum Dreieck in den Webseiten der Linkliste unten.
Ein Satz zum regelmäßigen
Siebeneck top
... |
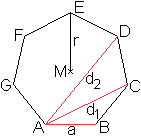Es gilt die Formel d1+d2-a=sqrt(7)r |
Herleitung
Man stelle sich vor, in den Eckpunkten eines Siebenecks liegen Punktmassen
m im Abstand r um eine Drehachse durch M.
>Dann ist das Trägheitsmoment bzgl. dieser Achse 7mr².
>Verschiebt man die Drehachse parallel nach A, so wird das Trägheitsmoment
AB²m+AC²m+AD²m+AE²m+AF²m+AG²m.
>Nach dem Satz von Steiner ist AB²m+AC²m+AD²m+AE²m+AF²m+AG²m
= 7MA²m+ 7mr².
Daraus folgt AB²+AC²+AD²+AE²+AF²+AG²
= 7MA²+ 7r² oder a²+d1²+d2²+d2²+d1²+a²=14r²
oder a²+d1²+d2²=7r².
>Nach dem Satz von Ptolemäus (s.o.) gilt d1d2=ad1+ad2
oder d1d2-ad1-ad2=0.
Es ist (d1+d2-a)²=d1²+d2²+a²+2(d1d2-ad1-ad2)=
d1²+d2²+a²=7r².
Dann ist d1+d2-a = sqrt(7)r, wzbw.
Quelle: (4)
Verschiedenes top
Figuren im Siebeneck
Hier wird besonders deutlich: Das Siebeneck ist achsensymmetrisch.
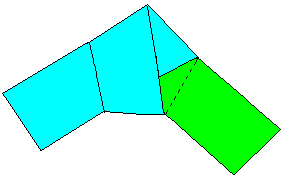
Unregelmäßige
Siebenecke aus Quadraten und gleichseitigen Dreiecken
Die beiden ersten Bilder folgen der Zerlegung 7=4+3.
Siebeneck-Knoten
... ...... |
 ... |
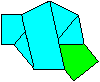So wie man aus einem Streifen Papier einen Fünfeckknoten bilden
kann, so auch einen Siebeneckknoten. |
Quelle: (3) Seite 57 f.
... ... |
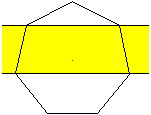Man erzeugt den Knoten am besten, indem man ein Siebeneck ausschneidet
und einen Streifen passender Breite herumwickelt. Anschließend kann
man das Siebeneck entfernen und den Streifen mit Hilfe der Faltlinien verweben. |
Regelmäßige
Siebenecke auf Münzen
... ... ... |
Alle Euromünzen sind rund bis auf das 20-Cent-Stück. Es hat
sieben Einkerbungen, die "Spanische Blume". |
Florian Pranghe teilte mir zur Spanischen
Blume als Münzsammler mit, dass die alte spanische 50-Peseten-Münze
auch diese Prägung hatte, um Blinden die Unterscheidung von anderen
Münzen zu erleichtern.
... ... |
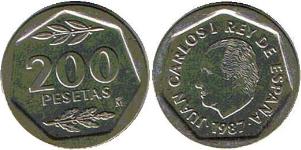Die alte spanische 200-Peseten-Münze enthält auf beiden Seiten
ein Siebeneck. |
... ...
|
Engländer hängen an ihrer Währung (2005).
Das 20-Pence- und das 50-Pence-Stück haben Siebeneckform.
Mehr auf meiner Seite Gleichdick. |
Perioden
... ... |
Periodische Erscheinungen veranschaulicht man gerne durch Vielecke.
Zur Periode 7 gibt es zum Beispiel die Wochentage und die Tonleiter. |
Siebeneck im Internet top
Deutsch
Joachim Mohr
Das Siebeneck,
die Dreiteilung des Winkels und die Kubikwurzel
Mathematikus
So kannst du ein regelmäßiges
Siebeneck falten und bauen.
NN (Lehrstuhl der Mathematik und ihre Didaktik, Universität Bayreuth)
Knoten regulärer
Vielecke
Ulrich Harsch (Hochschule Augsburg, bibliotheca
Augustana)
Matthäus
(Matheis) Roriczer
Wikipedia
Siebeneck, Heptagramm
Englisch
Eric W. Weisstein (MathWorld)
Heptagon,
Heptagonal
Triangle, Heptagon
Theorem, Trigonometry
Angles Pi7
Darren Abbey
Origami
heptagon
Dr.Math (Doctor Greenie. The Math Forum)
Curious
Property of a Regular Heptagon
Eric W. Weisstein (MathWorld)
Heptagon,
Heptagonal
Triangle
Jay Kappraff, Gary W. Adamson
A Unified
Theory of Proportion
"The heptagonal system is particularly rich in algebraic and geometric
relationships."
JIM ALISON
HEPTAGRAM CONSTRUCTION
John Page
Heptagon
Peter Steinbach
Golden
Fields: A Case for the Heptagon (.pdf file)
Robert Geretschläger
Folding the
regular heptagon (.pdf file)
Robin Hu
The Heptagon (Constructions)
Wikipedia
Heptagon, Heptagram
Referenzen top
(1) Bankoff, L. and Garfunkel, J. "The Heptagonal Triangle." Math.
Mag. 46, 7-19, 1973
(2) Robert Geretschläger: Folding the regular heptagon,
(im Internet verfügbar)
Crux Mathematicorum with Mathematical Mayhem, Vol 23, Nr. 2.März1997,
pp. 81-88
(3) H.Martyn Cundy, A.P.Rollett: Mathematical Models, Oxford 1961
(4) T. S. Tufton: ABCDEFG is a regular heptagon in a circle
of unit radius; to prove that AC+AD-AB=sqrt(7).
Mathematical Gazette 18, (1934) 274-275.
Feedback: Emailadresse auf
meiner Hauptseite
URL meiner
Homepage:
http://www.mathematische-basteleien.de/
©
2005, erweitert 2011, Jürgen Köller
top |
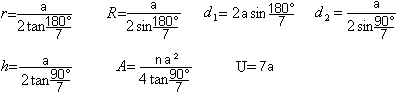
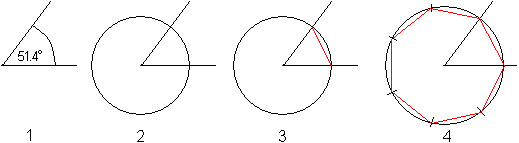
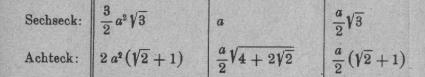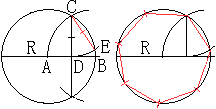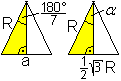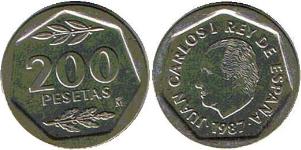