Fußpunktkurven
Inhalt dieser Seite
Was ist eine Fußpunktkurve?
Von der Kurve zur Fußpunktkurve
Fußpunktkurven des Kreises
Fußpunktkurven der Ellipse
Weitere Fußpunktkurven		 Gegenfußpunktkurve
Negative Fußpunktkurve
Fußpunktdreieck
Fußpunktkurven im Internet
.
Zur Hauptseite    "Mathematische Basteleien"

Was ist eine Fußpunktkurve?
...... Das wird an einem Beispiel erklärt.

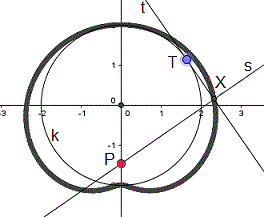
Gegeben sei die Kreislinie k und der Punkt P. 
Zeichnet man durch einen Kreispunkt T die Tangente t und fällt vom Punkte P aus das Lot auf die Tangente t, so entsteht der Schnittpunkt X. 
Bewegt sich der Punkt T auf der Kreislinie, so bewegt sich der Fußpunkt X des Lotes und beschreibt die "Fußpunktkurve".

Man ordnet also nach einer Vorschrift einer Kurve und einem festem Punkt P eine Fußpunktkurve zu. Bei de.wikipedia heißt die Webseite über die Fußpunktkurve deshalb Fußpunkt-Transformation. - Die englische Bezeichnung ist Pedal Curve. 
Auf dieser Webseite gebe ich das wieder, was ich bei einer ersten Begegnung mit Fußpunktkurven für bemerkenswert halte. 
Für die Zeichnungen verwende ich die "Dynamische-Geometrie-Software" (DGS) GeoGebra, auch in der Absicht, sie zu empfehlen. 
"GeoGebra ist kostenlos für nicht kommerzielle Nutzung."

Von der Kurve zur Fußpunktkurve       top
Vorweg wird an einem zweiten Beispiel - der feste Punkt P ist ein Kreispunkt - in fünf Schritten beschrieben, wie man in GeoGebra von einem Kurvenpunkt zu einem Punkt der Fußpunktkurve und schließlich zur vollen Fußpunktkurve gelangt.
1
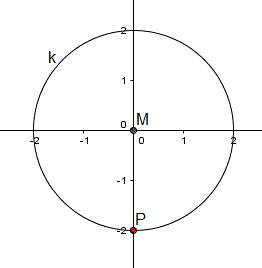...... Zeichne den Kreis k mit dem Radius r=2.
Markiere den Kreis und gehe oben links auf "Bewege um Punkt". 
Dann ändert sich der Kreis später nicht. 

Zeichne Punkt P(0|-2) und fixiere ihn auch. 
 

2
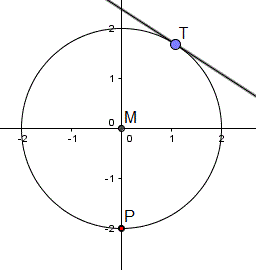...... Gib einen Kreispunkt T vor und zeichne durch ihn die Tangente.
3
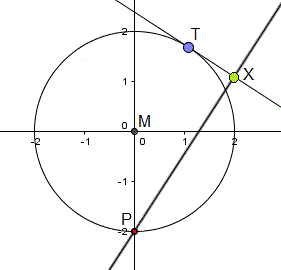...... Zeichne durch Punkt P die Senkrechte zur Tangente. Der Schnittpunkt sei Punkt X.
Er ist ein Punkt der gesuchten Fußpunktkurve.
4
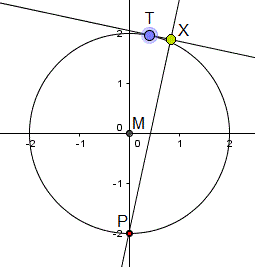...... Markiere Punkt T und gehe oben links auf "Bewege". So kann man Punkt T auf dem Kreis und mit ihm die Tangente, die Senkrechte und Punkt X  bewegen. Man gelangt zu allen Punkten X der  Fußpunktkurve. 
5
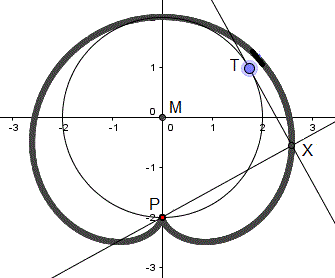...... Die Lage aller Punkte der Fußpunktkurve hält man fest, indem man mit dem Mauszeiger auf den Punkt X geht, die rechte Maustaste drückt und "Spur ein" einstellt. Bewegt man danach den Berührpunkt T auf der Kreislinie, dann wird die Fußpunktkurve als dicke Linie gezeichnet. 

Fußpunktkurven des Kreises       top
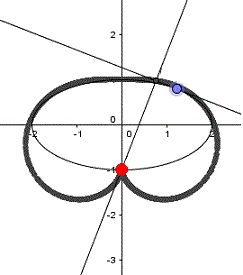
Gegeben sei ein Kreis und ein Punkt P. Wandert er von außen nach innen, so nimmt die Fußpunktkurve des Kreises verschiedene Formen an. 

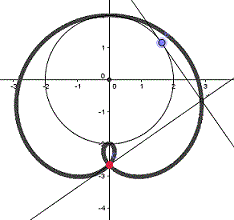
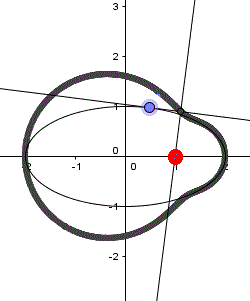
P liegt außerhalb der Kreises.

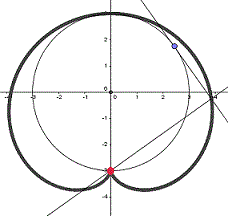
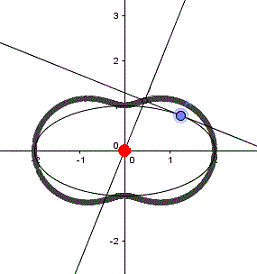
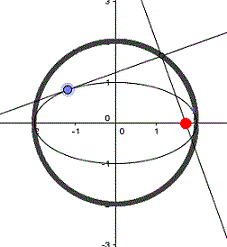
P liegt auf dem Kreis.

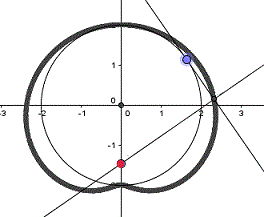
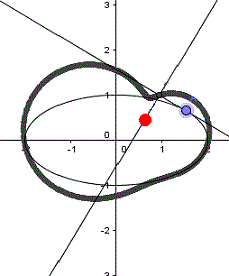
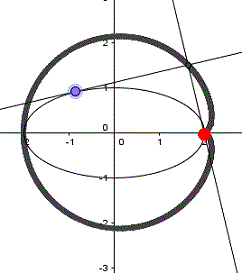
P liegt innerhalb der Kreises.

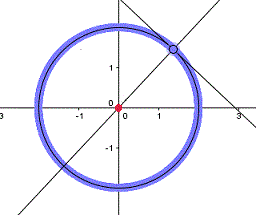
P liegt im Mittelpunkt des Kreises.

Die erste und die dritte Zeichnung zeigen verschiedene Formen der Pascalschen Schnecke, die zweite Zeichnung die Kardioide. In der vierten Zeichnung fallen die Kreislinie und die Fußpunktkurve zusammen.
Beschreibung durch eine Formel
Der Kreis mit dem Radius r sei in Parameterform gegeben: x = r cos(t) und y = r sin(t). Der feste Punkt P sei P(x0|y0).
Die Parameterform der Gleichung der Fußpunktkurve lautet 

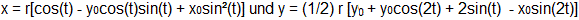
Quelle: http://mathworld.wolfram.com/CirclePedalCurve.html

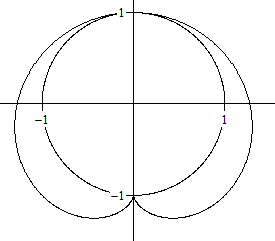... Für den Fall r=1 und P = P(0|-1) heißen die Gleichungen

x = cos(t) + cos(t)sin(t) und y = (1/2)[-1 - cos(2t) + 2sin(t)].

Das ist die Kardioide.

Fußpunktkurven der Ellipse       top
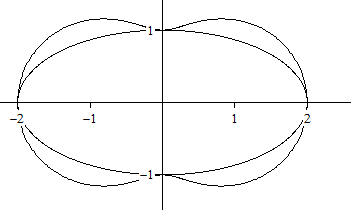
Die Fußpunktkurven der Ellipse sind vielfältiger als die des Kreises. 

Liegt der feste Punkt P in einem Brennpunkt der Ellipse, so ist die Fußpunktkurve ein Kreis.
Beschreibung durch eine Formel
Die Ellipse mit den Halbachsen a und b sei in der Parameterform x = a cos(t) und y = b sin(t)  gegeben. Der feste Punkt P sei P(x0|y0).
Die Parameterform der Gleichung der Fußpunktkurve lautet 

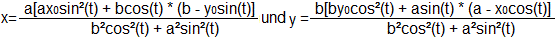
Quelle: http://mathworld.wolfram.com/EllipsePedalCurve.html 

... Für den Fall a=2, b=1 und P(0|0) lauten die Gleichungen 

x = [2cos(t)/[cos²(t)+4sin(t)] / [cos²(t) + 4sin(t)] 

und y = [4sin(t)] / [cos²(t) + 4sin(t)]. 

Weitere Fußpunktkurven top
Ich nenne jeweils den Namen der Ausgangskurve, die Gleichung und den festen Punkt. 

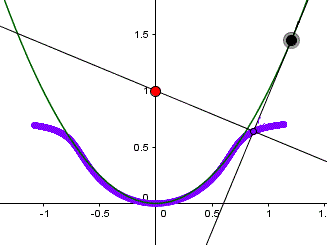
Parabel: y=x², P(0|1) 

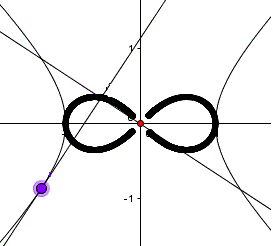
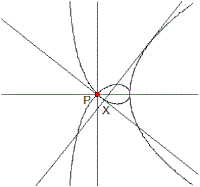
Hyperbel: x²-y²=1, P(0|0)

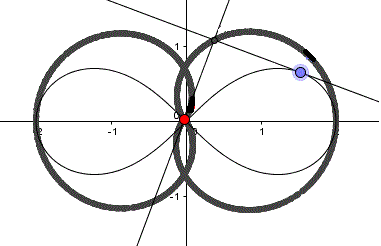
Lemniskate: (x²+y²)²=4(x²-y²),  P(0|0)


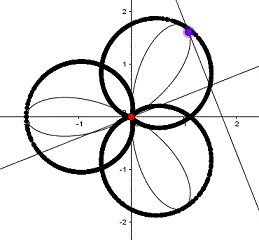
Trifolium: (x²+y²)(y²+2x)=8xy², P(0|0) 

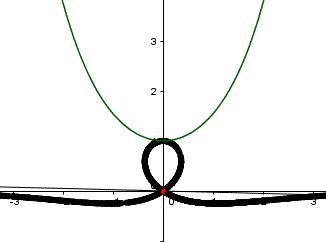
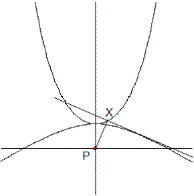
Kettenlinie: y = cosh(x), P(0|0) 

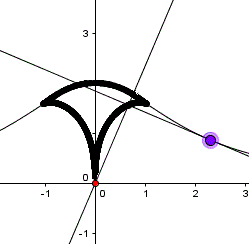
Versiera der Agnesi: y²(x²+4)=8, P(0|0)
Im Internet findet man Tabellen mit weiteren bekannten Kurven und ihren Fußpunktkurven. 
Ich verweise z.B. auf die Webseite Pedal Curve von MathWorld (URL unten) und die französische Webseite von Robert FERRÉOL (URL unten).
Das folgende Beispiel soll noch zeigen, wie verwickelt Fußpunktkurven sein können trotz einfacher Ausgangskurven.
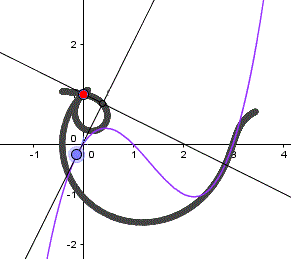... Gegeben sei der Graph der ganzrationalen Funktion f(x) = (1/2)x(x-1)(x-3).
Der feste Punkt sei P(0|1).

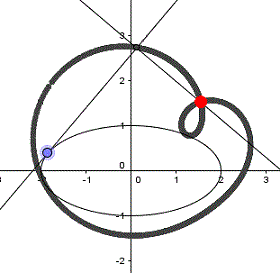
Gegenfußpunktkurve top
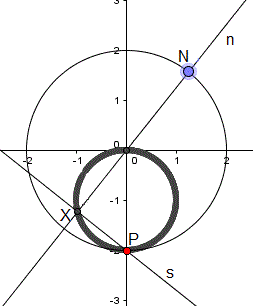... Zur Gegenfußpunktkurve gelangt man, indem man die Vorschrift zur Bestimmung der Fußpunktkurve abändert. Man zeichnet zu einem Kurvenpunkt N nicht die Tangente, sondern die Normale n.
Dann verfolgt man bei einer Bewegung des Kreispunktes N die Spur des Schnittpunktes X der Normalen n  mit der Senkrechten s. Die Gerade s steht senkrecht zu n und geht durch P. 

In diesem Falle ist die gegebene Kurve ein Kreis, der gegebene Punkt ein Kreispunkt und die resultierende Kurve ein Kreis mit halb so großem Radius. 

Die Gegenfußpunktkurve heißt im Englischen Contrapedal Curve.

Weitere Gegenfußpunktkurven 
Ich nenne jeweils den Namen der Ausgangskurve, die Gleichung und den festen Punkt. 

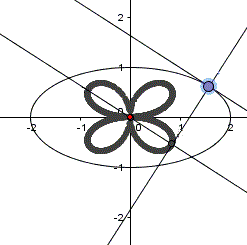
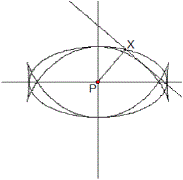
Ellipse: x²/4+y²/1=1, P(0|0)

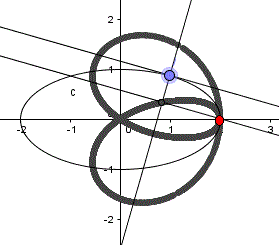
Ellipse: x²/4+y²/1=1, P(2|0)

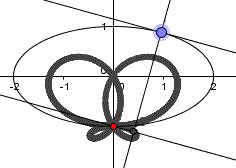
Ellipse: x²/4+y²/1=1, P(0|-1)

 

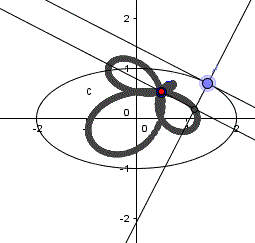
Ellipse: x²/4+y²/1=1, roter Punkt

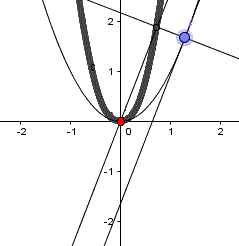
Parabel: y=x², P(0|0) 

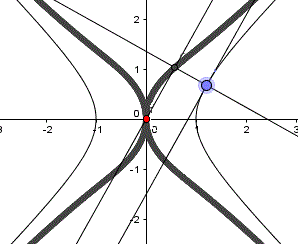
Hyperbel: x²-y²=1, P(0|0)
"The contrapedal curve is the pedal curve of the evolute of a given curve (Zwikker 1963, p. 151)".
Gefunden bei MathWorld 

Negative Fußpunktkurve top
Aus einer Kurve und einem festen Punkt leitet man nach einer weiteren Vorschrift die Negative Fußpunktkurve her. 
Dazu folgen zwei Beispiele, bearbeitet mit GeoGebra.
Negative Fußpunktkurve der Kardioide
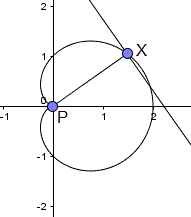...... Gegeben seien die Kardioide durch die Gleichung (x²+y²-x)² = x²+y² und der Punkt P(0|0).

Man wählt einen beliebigen Kurvenpunkt X und verbindet ihn mit Punkt P, also dem Nullpunkt. 
Dann zeichnet man durch den Kurvenpunkt X eine Senkrechte.

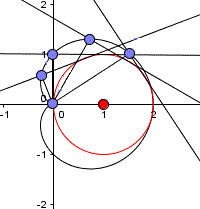...... Wählt man verschiedene Kurvenpunkte und zeichnet jedes Mal die Strecke und die Senkrechte, so werden diese zu Tangenten eines Kreises. 
Dieser Kreis ist die Negative Fußpunktkurve.
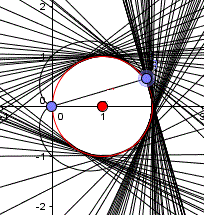...... Bewegt man den Punkt X auf der Kreislinie, so bewegen sich mit ihm die Senkrechten. Markiert man eine Senkrechte, drückt die rechte Maustaste, wählt Eigenschaften, setzt im geöffneten Fenster ein Häkchen bei "Spur anzeigen" und schließt das Fenster, so werden bei Bewegung des Punktes X die Senkrechten gezeichnet. Dabei bestimmt die Geschwindigkeit der Bewegung die Anzahl der Senkrechten. 
Eine gleichförmige Bewegung ist mir nicht gelungen, doch der Kreis kommt gut heraus.
Negative Fußpunktkurve der Normalparabel
Für die Normalparabel mit y=x² und dem festen Punkt P(0|0) kann man die Parametergleichung der Geradenschar relativ einfach bestimmen. 
Es sei X(a|a²) ein beliebiger Parabelpunkt. Dann wird eine Gerade durch den Punkt X durch die Gleichung y=ax beschrieben. 
Die dazu senkrechte Gerade gehorcht der Gleichung (y-a²)/(x-a) = -1/a. Das führt zu y=-(1/a)x+(1+a²). 
Mit GeoGebra kann man eine Geradenschar kontrolliert so zeichnen:
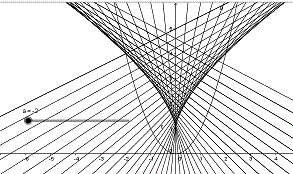... > Gib in die letzte Zeile y=-(1/a)x+1+a² ein und bestätige die Eingabe.
Es erscheint eine Gerade und ein Schieberegler.
> Markiere den Regler, drücke die rechte Maustaste und gehe auf Eigenschaften.
> Stelle -2 bis 2 ein und Schrittweite 0.1. Schließe das Fenster.
> Markiere die Gerade, drücke die rechte Maustaste und gehe auf Eigenschaften.
> Markiere "Spur anzeigen". Schließe das Fenster.
Bewege den Punkt des Schiebereglers. Die Geradenschar wird gezeichnet.
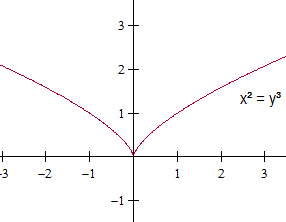... Die negative Fußpunktkurve ist ein Graph aus der Schar der neilschen Parabeln. 
Ich benutze meist das Programm WinPlot. Auch da kann man die Geradenschar kontrolliert zeichnen. 
Man geht so vor: Man wählt Fenster/2-dim/Gleichung/1.y=f(x) und gibt y=-(1/a)x+1+a² ein. Nach OK öffnet sich das Fenster "Inventar". Da wählt man "Schar" und gibt  -2 bis 2 und Schrittweite 10 ein.

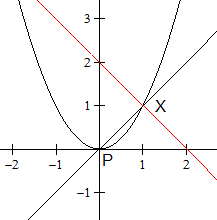
y=x und y=-x+2

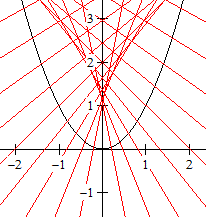
y=-(1/a)x+1+a² mit -2<a<2 und Schrittlänge 20
Weitere Negative Fußpunktkurven 
Ich nenne jeweils den Namen der Ausgangskurve, die Gleichung und den festen Punkt. 

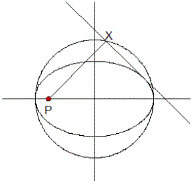
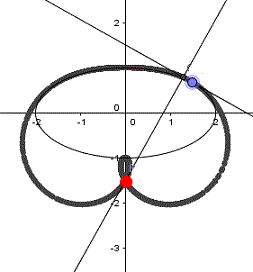
Kreis: x²+y²=1, roter Punkt 

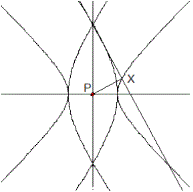
Hyperbel: x²-y²=1, P(0|0)

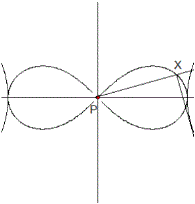
Lemniskate: (x²+y²)²=4(x²-y²),  P(0|0)

Gerade Strophoide: y²=x²(1-x)/(1+x), P(0|0) 

Kettenlinie: y = cosh(x), P(0|0) 

Ellipse: x²/4+y²/1=1, P(0|0)

Quelle: http://www-groups.dcs.st-and.ac.uk/history/Curves/Curves.html

Mehr über Negative Fußpunktkurven auf der Webseite Negative Pedal Curve von MathWorld (URL unten)

Fußpunktdreieck top
Das sollte noch erwähnt werden. 
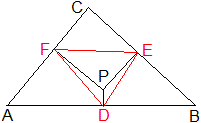...... Gegeben sei das Dreieck ABC und ein Punkt P innerhalb des Dreiecks. 
Fällt man von Punkt P aus die drei Lote auf die Seiten des Dreiecks, so bilden die Fußpunkte das Fußpunktdreieck.
Mehr auf meiner Seite Gleichseitiges Dreieck.

Fußpunktkurven im Internet       top

Deutsch

Alexandra Moese  (Zusammenfassung der Diplomarbeit) 
Konstruktionen spezieller Kurvenpaare und deren Untersuchung mit Mathematica

Wikipedia 
Fußpunkt-Transformation, Kardioide, Pascalsche Schnecke,  Neilsche Parabel,   Fußpunktdreieck,   Kaustik (Optik), Evolute, GeoGebra

Englisch

Eric W. Weisstein  (MathWorld)
Pedal Curve,  Circle Pedal Curve, Ellipse Pedal Curve,  Contrapedal Curve,  Negative Pedal Curve,  Cardioid Pedal Curve

Jan Wassenaar
Pedal curve

Richard Parris (Freeware-Programme) 
winplot

Wikipedia
Pedal curve,  Pedal equation,  Negative pedal curve,  Cardioid, Limaçon, Pedal triangle, Negative pedal curve, 
Evolute, Caustic (Mathematics)

Xah Lee
Pedal Curve

Französich

Robert FERRÉOL
PODAIRE D'UNE COURBE

 Feedback: Emailadresse auf meiner Hauptseite

URL meiner Homepage:
https://www.mathematische-basteleien.de/

©  Januar 2016 Jürgen Köller

top
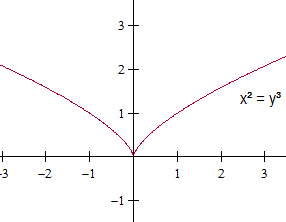
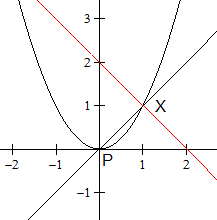