Was ist die Exponentialfunktion?
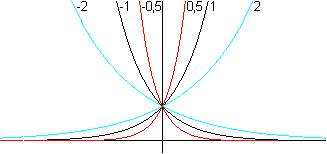
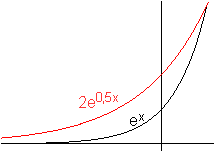
Im engeren Sinne ist die Exponentialfunktion die Funktion f mit f(x)=ex, wobei e die eulersche Zahl e=2,71828... ist. Sie heißt auch e-Funktion und der Funktionsterm auch exp(x). Die Funktion mit f(x)=ex ist Thema dieser Webseite. Graph top
Eulersche Zahl top
Deutlicher wird dieses Verhalten, wenn man die ersten Glieder der Folge a(n)=(1+1/n)n ausrechnet.
Beweis Trotz dieser Überlegungen muss die Existenz der Zahl e bewiesen werden. Geeignet dazu ist das erste Konvergenzkriterium "Jede beschränkte und monotone Zahlenfolge ist konvergent". Es muss also bewiesen werden, dass die Folge a(n)=(1+1/n)n für n gegen Unendlich nach oben und unten beschränkt und monoton (steigend) ist. Binomische Formel Ausgangspunkt ist die binomische Formel. Sie lautet: (a+b)n=C(n,0)anb0+C(n,1)an-1b1+C(n,2)an-2b2+...+C(n,n-2)a2bn-2+C(n,n-1)a1bn-1+C(n,n)a0bn mit (1+1/n)n =C(n,0)*1+C(n,1)(1/n)+C(n,2)(1/n²)+...+C(n,n-2)/(1/nn-2)+C(n,n-1)/(1/nn-1)+C(n,n)/(1/nn). Untere Schranke Da jeder Summand positiv ist, gilt a(n)>0. Obere Schranke Zur Bestimmung einer oberen Schranke muss man etwas weiter ausholen. Die binomische Formel lautet in der vertrauten Schreibweise "n über k" und mit dem Summensymbol 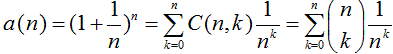 . .... 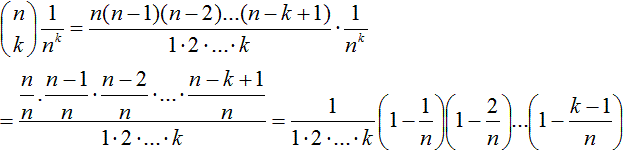
Dann gilt ... 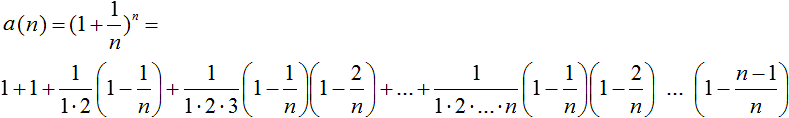 . .
Man schätzt die Summe ab. Ersetzt man jeden Klammerterm durch 1, so vergrößert man die Summe.
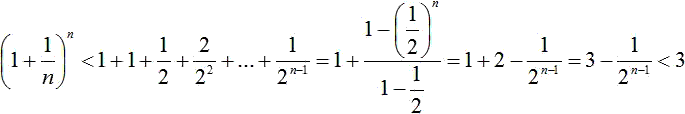 . .Ergebnis: Die Zahl 3 ist eine obere Schranke. Es gilt a(n)<3 für hinreichend große Zahlen n. Monotonie Zu zeigen ist a(n+1)>a(n). Dazu berechnet man analog zu a(n) die Summe für a(n+1). Es gilt ... 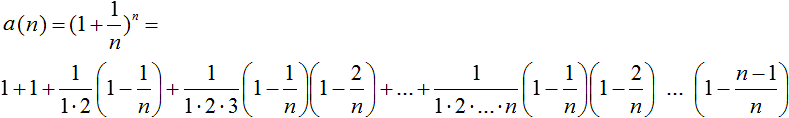 . .
Dann ist in Analogie dazu ... 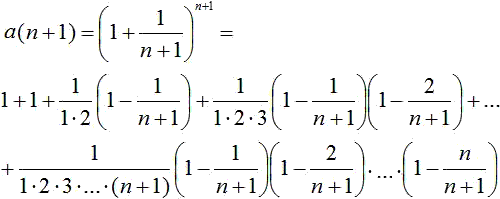 . .
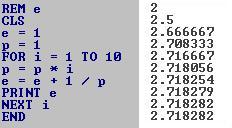
Zuerst stellt man fest, dass a(n+1) einen Summanden mehr hat. Außerdem ist in den Klammern der Nenner n+1 jeweils kleiner der Nenner n. Es wird also in der Summe von a(n+1) von 1 weniger subtrahiert. Daraus folgt, dass a(n+1)>a(n) gilt. Quelle: (2), Seite 98ff. Eulersche Zahl als Dezimalzahl Die eulersche Zahl ist eine transzendente Zahl und kann nur näherungsweise als Dezimalzahl angegeben werden, dann aber in gewünschter Genauigkeit. Der Taschenrechner TI 30 zeigt e=2.718281828. Auf einer Webseite der Universität
von Utah (URL unten) wird die Zahl e auf 10.000 Ziffern genau angezeigt.
Das sind die ersten 50 Dezimalen.
Ableitung top
Zum Beweis
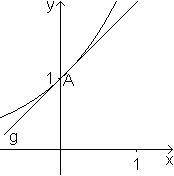
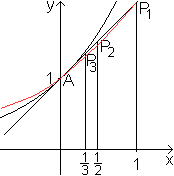
Der Graph von y=a2x verläuft durch P2(1/2|1+1/2); das bedeutet a2 =(1+1/2)2. ... Der Graph von y=anx verläuft durch Pn(1/n|1+1/n); das bedeutet an =(1+1/n)n. Daraus folgt: Geht n gegen Unendlich, so geht Pn gegen A(0|1) und an gegen e. Ergebnis: Die Gerade berührt die Kurve in A(0|1) und damit ist die Steigung im Punkte A(0|1) gleich 1.
Damit ist die Hauptarbeit getan. Ein letzter Schritt folgt. ... 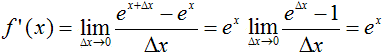
Das war zu beweisen. (1) Taylor-Reihe top
Für die Exponentialfunktion gilt f(0)=f '(0)=f ''(0)=f '''(0)= ... = 1 Dann ist ex= 1 + x/(1!) + x2/(2!) + x3/(3!) + x4/(4!) + ... oder ex = 1+x+(1/2)x2+(1/6)x3+(1/24)x4+(1/120)x5+(1/720)x6+(1/5040)x7+ ... . Setzt man x=1, so erhält man die Darstellung der Zahl e durch die Reihe e==1+1+(1/2)+(1/6)+(1/24)+(1/120)+(1/720)+(1/5040)+ ... .
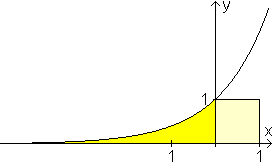
Stammfunktion top
Und das ist eine Veranschaulichung der Ergebnisse.
 Bekannte Funktionen
top
Hyperbelfunktionen
Mehr über die Funktion Cosinus Hyperbolicus findet man auf meiner Webseite Kettenlinie.
Umkehrfunktion top
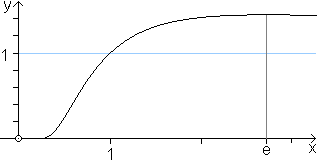
Behauptung: Die Ableitung der Funktion g(x)=ln(x) ist g'(x)=1/x. Herleitung Es gilt y=ln(x) oder x=ey. Für die Ableitung gilt allgemein g'(x)=1/f'(y), hier also [ln(x)]'=1/(ey)=1/x, wzbw.. Allgemeine
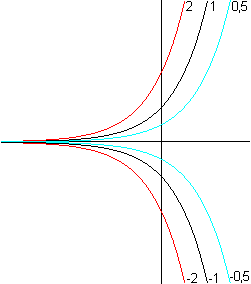
Exponentialfunktion top
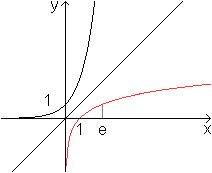
Oben wurde die Funktion mit f(x)=ax (a>0) als allgemeine Exponentialfunktion vorgestellt. Sie ist auch eine Exponentialfunktion, denn es gilt f(x)=ekx mit k=ln(a). Zum Beweis Es ist zu zeigen: eln(a)x =ax oder [eln(a)]x =ax. Diese Gleichung ist richtig, weil eln(a)=a ist. Ergebnis: Man kann die Funktion f(x)=ax (a>0) als f(x)=eln(a)x schreiben. Steiners Problem top
Es gilt f(x)=x(1/x)=e(1/x)ln(x). Dann ist f '(x)=[(1/x)ln(x)]'*e(1/x)ln(x)=[(1/x²)-(1/x²)ln(x)]e(1/x)ln(x)=(1/x²)[1-ln(x)]e(1/x)ln(x). Dann ist f '(x)= 0 für ln(x)=1 oder x=e, wzbw.. Es gilt ferner lim[n(1/n)]=1 für n gegen Unendlich. (3) Seite 421.f Zerfallsgesetz top
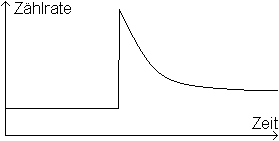
Betrachtet man eine Probe mit N instabilen Kernen, so hängt die Abnahme dN/dt instabiler Kerne im statistischen Mittel von der Anzahl N ab, und zwar ist dN/dt~N. Das führt zum Ansatz dN/dt= -kN(t) oder N'(t)= -kN(t). Die Variable k ist eine Konstante. Diese Differentialgleichung wird gelöst von der Exponentialfunkton N(t)=N0e-kt. Die Variable N0 wird durch die Anfangsbedingungen festgelegt. Zum Zeitpunkt t=0 ist N=N0. Setzt man N(t)=(1/2)N0 in die Gleichung N(t)=N0e-kt, so ist (1/2)N0=N0e-kT1/2. Das führt nach Logarithmieren der Gleichung zu ln(1)-ln(2)= -k T1/2 oder k==ln(2)/T1/2 oder k=0,693/T1/2. Das ist so zu deuten: Ist im Mittel die Hälfte der instabilen Kerne zerfallen, so ist die "Halbwertszeit" T1/2 verstrichen. Die Halbwertszeit ist eine kennzeichnende Größe radioaktiver Stoffe. Ergebnis: Das Zerfallsgesetz ist N(t)=N0e -(0,693/T1/2)*t. 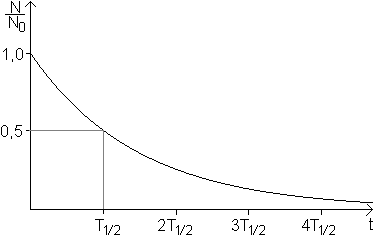 Gerne würde ich an dieser Stelle eine Abbildung aus dem Computermagazin 64'er aus den 1980er Jahren zeigen. Wächter über das Atomkraftwerk Grohnde bei Hameln verfolgten über Monate die radioaktive Strahlung in der Nähe. Mit einem Geigerzähler und dem Homecomputer C64 registrierten sie sie und erfassten auch zufällig den dramatischen Anstieg nach der Tschernobyl-Katastrophe von 1986.
Schlussbemerkung top
So wird die Routine der ganzrationaler Funktionen verlassen. Die Schüler lernen mit der Exponentialfunktion eine weitere Klasse von Funktionen mit vielen Anwendungen kennen. Exponentialfunktion im Internet top Deutsch Matroids Matheplanet
Wikipedia
Englisch Eric W. Weisstein (MathWorld)
Peter Alfeld (Department of
Mathematics, University of Utah)
Richard Parris (Freeware-Programme)
Wikipedia
Referenzen
top
URL meiner
Homepage:
© September 2012 Jürgen Köller |
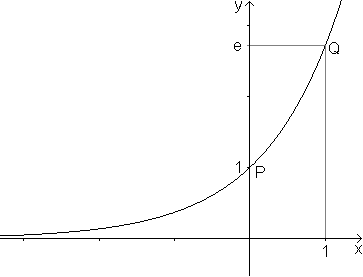 ...
... ...
... ...
... ...
...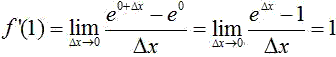
 ...
...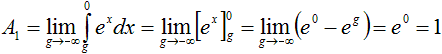
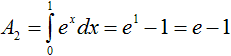
 ...
...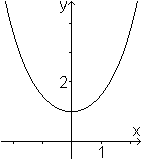
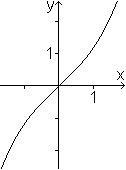
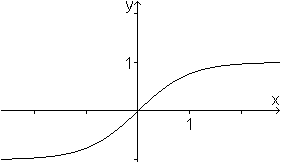
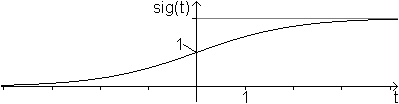
 ...
...
 ...
... ...
...