Was ist Bellmans Problem Verirrt im Wald? (Englisch: Bellman's lost in a forest problem) 

Ein Wanderer verirrt sich in einem Wald, dessen Form und Ausmaße ihm genau bekannt sind. Welcher Weg ist der beste, um aus dem Wald heraus zu kommen? (1)
Auf dieser Seite geht es nur um einen Sonderfall: Die Form ist ein Kreis, der Startpunkt ist der Mittelpunkt des Kreises. 

Wie kommt es zu dieser Seite?     top
Mir wurde das folgende Rätsel zugesandt, das beim Geocaching gefunden wurde. 
"Poldi hat sich im Wald verlaufen. Alles, was er weiß, ist Folgendes: Er befindet sich genau 500 Meter vom Waldrand eines riesigen Waldes entfernt. Der Wald wird von einer Geraden begrenzt. Leider weiß Poldi nicht, in welcher Richtung sich der Rand des Waldes befindet.
Wie viele Zentimeter muss Poldi mindestens zurücklegen, um auf jeden Fall aus dem Wald heraus zu finden?"

Erste Überlegung top

Der Startpunkt ist der Mittelpunkt des Kreises mit dem Radius r=500 m.  Die möglichen Waldränder sind Tangenten an den Kreis.

......

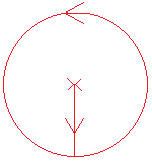Poldi erreicht sicher den Waldrand, wenn er radial in eine beliebige Richtung geht und dann den Kreis abläuft.  Der Weg ist w = r+2*pi*r oder angenähert 7,28r. Da es sich um ein Geocaching-Rätsel handelt, erfährt man nur, ob die Lösung falsch oder richtig ist.  Diese Lösung ist falsch.

Zweite Überlegung top

......

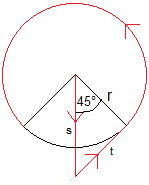Offenbar muss Poldi den Kreis verlassen. Dann bietet sich der folgende Weg an. Er geht radial über einen möglichen Waldrand hinaus, dreht sich um 45° und erreicht auf einer Tangente den Kreis. Dann geht er den Kreisbogen zu 270° ab. Der Weg beträgt w(45°)=s+t+[(270°/360°)(2*pi)]r = sqrt(2)r+r+(3/2)*pi*r oder angenähert 7,12r.

......

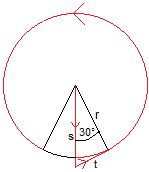Ist der Drehwinkel 60°, so gilt w = [s+t+(300°/360°)*(2*pi)]r. Für s und t gilt cos(30°)=r/s oder s=(2/3)sqrt(3)r und tan(30°)=t/r oder t=(1/3)sqrt(3)r. Dann ist w(30°) = [(2/3)sqrt(3)+(1/3)sqrt(3)+(5/3)*pi]r = [sqrt(3)+(5/3)*pi]r oder angenähert w=6,96r. .......................

Der Weg ist w = s+t+(2*pi*r-2xr).
Für s und t gilt cos(x)=r/s oder s=r/cos(x) und tan(x)=t/r oder t=r*tan(x). 
Dann ist w = r/cos(x)+r*tan(x)+2*pi*r-2xr = [1/cos(x)+tan(x)+2*pi+2x]r.

Die Formel kann als eine Funktionsgleichung aufgefasst werden, 
w(x) = 1/cos(x)+tan(x)+2*pi-2x. (Es sei o.E.d.A. r=1.)
Das Problem führt zu einer Extremwert-Aufgabe, bei der ein Winkel mit minimalem Weg gesucht wird. 

Der Graph weist darauf hin, dass (geschätzt) in x=0,5 oder alpha=[x/(2*pi)]*360°=18° eine Minimalstelle liegt und der Weg w=7r ist.

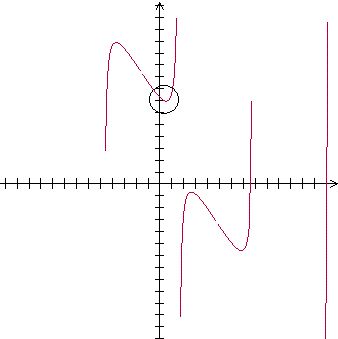
Das bestätigt die Rechnung.
Die Funktion w(x) hat eine Minimalstelle x, wenn w'(x)=0 und ferner w''(x)>0 gilt.
Es gilt also w'(x) = sin(x)/cos²(x)+1/cos²(x)-2 
und dann sin(x)/cos²(x)+1/cos²(x)-2 = 0 und sin(x)+1-2cos²(x) = 0 und sin(x) +1-2*[1-sin²(x)]=0 und sin²(x)+(1/2)sin(x)-1/2 = 0.

Das ist ein quadratische Gleichung in sin(x).
Mit y=sin(x) ist y²+(1/2)y-1/2= 0 und y_1'2=-1/2+-sqrt[(1/4)+1/2)] oder y_1'2 = -1/2+-(1/2)sqrt(3).
Die Lösung ist sin(x) = 1/2sqrt(3)-1/2.
Näherungsweise gilt x=0,366 oder alpha=20,9°.
Für den Weg ergibt sich w=[1/cos(20,9°)+tan(20,9°)+2*pi-2*0,366]r = 7,00r.

Auch diese Lösung ist falsch.

Isbell's path   top
Recherchen im Internet führen zur Lösung des Problems, siehe (1) und (2).

......

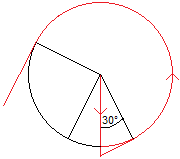Der Weg beginnt wie oben für alpha=30°, es folgt der Kreisbogen zu 210°. Dann wird der Kreis verlassen und der Weg endet mit der Länge r auf einer Tangente. Das ist die entscheidende Idee. Der Weg ist dann w=s+t+(210°/180°)*pi*r = [sqrt(3)+(7/6)*pi+1]r oder angenähert 6,40r.

Schlussbemerkung top
Man sollte nicht meinen, als sei Bellmans Problem eine mathematische Spielerei. Mathematiker haben sich ernsthaft um eine Lösung bemüht. Dabei sind viele Formen mit unterschiedlichen Startpunkten erfolgreich untersucht worden. Eine Übersicht findet man auf der Webseite (1).
Bellmans Problem gehört in der allgemeinen Formulierung zu den ungelösten Problemen der Mathematik.

Bellmans Problem Verirrt im Wald im Internet     top

Englisch

Steven R. Finch and John E. Wetzel
Lost in a Forest

stack exchange communities
Can this ant find its way back to the nest?

Wikipedia
Bellman's lost in a forest problem