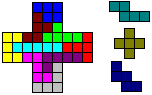
What are Pentominoes?
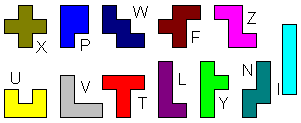 ... ... |
You call the 12 figures, which you can make of five squares,
pentominoes.
You must arrange the squares, so that they must have
in common at least one side.
The shapes are similar to capital letters, so they have
letters as names. |
Building Rectangles
top
The main problem of the pentomino 'research' is to combine
12 pieces to rectangles.
You can form four different rectangles:
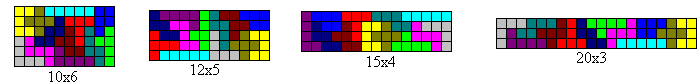 The rectangles have 2339 solutions (6x10), 2 solutions
(3x20), 368 solutions (4x15), 1010 solutions (5x12).
The rectangles have 2339 solutions (6x10), 2 solutions
(3x20), 368 solutions (4x15), 1010 solutions (5x12).
 You can form a rectangle 5x13, if you leave blank a pentimono
(5x13 = 65 = 60 + 5).
You can form a rectangle 5x13, if you leave blank a pentimono
(5x13 = 65 = 60 + 5).
Building New Figures
top
You can design more figures beside rectangles. Best you
don't plan a pattern, but start working. Then it is easier to discover
new figures.
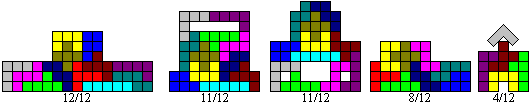 The results are the figures:
The results are the figures:
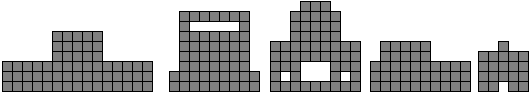
There are no limits for your fantasy.
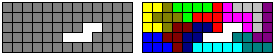
Figures with Holes
top
You can form a chessboard 8x8, if you admit 4 holes.
(8x8-4=60) (drawing 1).
You can derive new problems:
> Rectangles with isolated holes (drawing 2),
> Figures with as much as possible isolated holes (drawing
3). There are only two solutions with 13 holes (book 2).
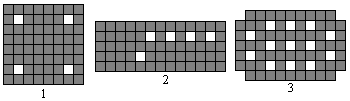 Solutions:
Solutions:

Magnification
Problems top
Pentominoes with triple magnification:
... ... ... |
... ... ... |
|
You build a pentomino with triple magnification. You
need nine pieces. Three pieces are left. |
... ... ... |
It is more difficult not to use the pentomino concerned. |
.. ..... .....
|
You can skip one pentomino in a triple pentomino and
fill up the rest with eight pentominoes. Four Pentominoes are left. |
Double Pentominoes:
..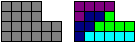 ..... .....
|
You can imitate some compact pentominoes in double size.
You need four pieces, eight ones are left. |
Darian Jenkins sent me the
following datas.
Number of ways to duplicate a pentomino using four pieces
Dup F =
1 |
Dup I =
2 |
Dup L =
8 |
Dup N =
7 |
Dup P =
50 |
Dup T =
1 |
Dup U =
7 |
Dup V =
0 |
Dup W =
5 |
Dup X =
0 |
Dup Y =
2 |
Dup Z =
7 |
Number of ways to triplicate a pentomino using any nine
of the twelve pieces
| Trip F = 443 |
Trip I = 201 |
Trip L = 938 |
Trip N = 610 |
Trip P = 9144 |
Trip T = 382 |
Trip U = 444 |
Trip V = 482 |
Trip W = 202 |
Trip X = 20 |
Trip Y = 809 |
Trip Z =
395 |
Number of ways to triplicate a pentomino not using the
piece being replicated
| Trip F = 125 |
Trip I = 19 |
Trip L = 113 |
Trip N = 68 |
Trip P = 497 |
Trip T = 106 |
Trip U = 48 |
Trip V = 63 |
Trip W = 91 |
Trip X = 15 |
Trip Y = 86 |
Trip Z =
131 |
Rings top
You can make rings of pentominoes, build bridges or make
other figures, in order to surround as many squares as possible.
- Students of the Belgian school TID in Ronse and their
teacher Odette de Meulemeester have specialized in these problems.
(URL http://pentomino.classy.be/indexnl.html).
- The ring on the left includes 120 squares. There
is a ring with 128 squares (URL: http://www.iread.it/lz/maximizing.html).
- The bridge on the right includes 251 squares.
There is a bridge with 278 squares (8).
Once Again: Rectangles
top
...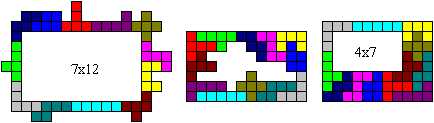 ... ... |
You can also lay pentominoes, so that the inside or the
border form rectangles.
Both is possible, too. |
There are 84 squares inside on the left, 90 are maximum.
(Book 6, W.F.Lunnon)
From
the Pentomino to the Pentacube top
... ... ... |
Pentomino pieces are mostly not two-dimensional, but
are made of cubes and form pentacubes in the plain. They are easier to
manage and make new 3D-puzzles possible. |
Boxes
of Pentacubes top
The main problem is forming boxes.
You can lay three:
Solutions:
The boxes have the measurements 3x4x5
(3940 solutions), 2x5x6 (264 solutions)
oder 2x3x10 (12 solutions).
Large
Pentacubes
top
You imitate a pentomino with double magnification and
triple height. A solution of the T-Pentomino follows.
Number of solutions: W (0), X(0), F(1), T(3), Y(7),
U(10), I(12), V(21), Z(24), N(51), L(99), P(1082).
More Figures
of Pentacubes top
You can design more complicated 3-D-shapes and build
them with pentominoes.
A tower with a hole in the middle follows as an example.
There are no limits for your fantasy.
Datas of the
Pentacubes
top
Meaning of the numbers:

|
V volume, O surface area, K sum
of edges
k number of edges, e number of corners,
a
number of sides |
There is the formula e + a - k = 2. (Thanks to 6c,
7a, 7c, 7d from 99/00)
More Pentacubes top
. .. .. |
There are 17 three-dimensional pentacubes besides the
standard ones. Five are symmetric with a plane (pink). The remaining pentacubes
appear as pairs of symmetric mirror solids. Three pairs have three
cubes in line (blue), three only two cubes (green). |
Making of Pentominoes
top
If you want to play with pentominoes you have to make
them with your hands.
Squares of cardboard will do because many problems are
restricted to two-dimensional figures.
You can make pentominoes of cubes. You buy a length of
wood which is square in cross-section, cut it into cubes and glue the cubes
together.
Another method is glueing dice. The best thing is to use
a two component glue, because it needs time to harden. Then you can form
the pentominoes without having to hurry.
A cheap method is making them from a sheet of paper. You
must design a base of every pentomino and fold it.
Pentominoes im
Internet top
German
Andrew Clarke
Polyominoes
B.Berchtold
Pentominoes
- Lösung 6x10 - Applet Online
Dr. Nagy László
Pentomino
HungarIQa
Das Element der Pentominoes ist kein Quadrat mehr,
sondern ein Rhombus. Puzzle-Aufgaben mit jetzt 20 Pentominoes
Thimo Rosenkranz
Pentomino-Figuren
Wikipedia
Pentomino,
Polyomino
English
Andrew Clarke
Polyominoes
c.w.ricken
play pentacubes online
David J. Eck
Pentomino
Solver(8x8 with 4 holes), Applet
Eithan Samara
Pentominoes-3D
Solver
Eric W. Weisstein (MathWorld)
Pentomino,
Polyomino
Gerard's Home Page
Gerard's
Universal Polyomino Solver
Kevin Gong
The
Mathematics of Polyominoes
Michael Reid
Michael
Reid's polyomino page
Miroslav Vicher (Miroslav Vicher's Puzzles Pages)
Polyominoes
Snaffles home page
Pentomino
Relationships
Torsten Sillke
Tiling
and Packing results
Wikipedia
Pentomino,
Polyomino
Russian
Leonid Mochalov [PUZZLES of LEONID MOCHALOV]
Puzzles
with Polyominoes
References (German)
top
(1) Martin Gardner: Mathematical Puzzles & Diversions,
New York 1959
(2) bild der wissenschaft 7/1976
(3) Pieter van Delft, Jack Botermans: Denkspiele der
Welt, München 1980
(4) Martin Gardner: Bacons Geheimnis, Frankfurt a.M.
1986 (Polywürfel)
(5) R.Thiele, K.Haase: Der verzauberte Raum, Leipzig,
1991
(6) Jens Carstensen: Legespiele, MU26:2 1980 (Seite 5
bis 36)
(7) Solomon W.Golomb: Polyominoes, Princeton, New Jersey
1994 (ISBN0-691-08573-0)
(8) Pieter Torbijn: Pentominos Bridges, Cubism For Fun
59, November 2002
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
1999 Jürgen Köller
top |