|
Was ist das magische Ei?
... ... ... |
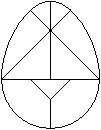 ... ...
|
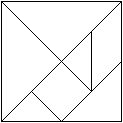
Das magische Ei ist ein Puzzle ähnlich dem
Tangram.
Es entsteht, wenn man statt eines Quadrates eine Ei-Figur
aufteilt.
Das magische Ei heißt auch Ei des Columbus
und im Englischen auch Scrambled Egg. |
... ... ... |
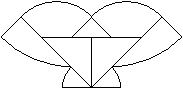 ... ... |
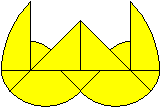
Eine Aufgabe besteht darin, eine vorgegebene Figur aus
den neun Stücken nachzubauen.

|
Es ist vielleicht interessanter, eigene Figuren zu erfinden.
Sinnigerweise findet man in der Literatur
und im Internet fast nur Vögel. Logisch, sie schlüpfen aus Eiern.
Anker-Geduldspiele
top
Eigentlich sollte ich aus historischen
Gründen diese Webseite besser in Ei des Columbus umbenennen.
In Buch (4) kann man u. a. Folgendes
nachlesen.
Schon ab 1882 produzierte die Firma Richter aus Rudolstadt
große Mengen an Tangram-ähnlichen Spielen verschiedenster Form,
die Anker-Puzzles.
... ... ... |
Darunter war auch das magische Ei unter dem Namen
Ei
des Columbus. Später hieß es auch Wunderei.
Interessant war das Material, aus dem die "Steine" hergestellt
wurden.
Die rote Ziegelmasse bestand aus Kaolin, Sand und Leinöl. |
Die Silhouette des fliegenden
Vogels oben stammt aus einem Anleitungsbuch der Ankerwerke.
...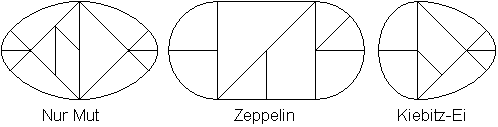 ... ... |
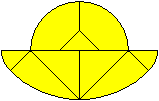
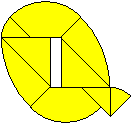
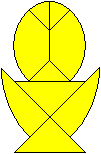
Aus Gründen der Wirtschaftlichkeit verwendete man
möglichst die gleichen Formen für das zeitweise 36 Tangram-Spiele
umfassende Sortiment.
Das demonstrieren die drei ovalen Varianten. |
Durch meine Homepage bin
ich in Kontakt zu Puzzle-Sammlern gekommen. Sie schätzen sich glücklich,
wenn sie in ihrer Sammlung auch historische Anker-Puzzles (bzw. Anchor
Puzzles) mit möglichst wenig beschädigten Steinen und möglichst
in Original-Verpackung besitzen.
In Rudolstadt werden noch
heute einige Tangram-Spiele aus Ziegelmasse produziert, darunter auch das
Ei des Columbus. Unten gebe ich einen Link auf die Homepage der Firma Anker
Steinbaukasten GmbH an.
Eine Variante top
...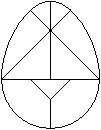 ... ... |
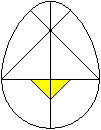 ... ... |
Es liegt nahe, dass man das kleine Dreieck halbiert,
so wie der Viertelkreis oben auch halbiert wird.
So gelangt man zu einem Puzzle aus zehn Stücken,
das viele neue Figuren ermöglicht.
Für diese Variante bietet Michael Bischoff im Internet
(URL unten) eine umfangreiche Sammlung von Vögeln. |
Herstellung
der Ei-Figur top
...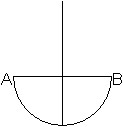 |
Zeichne einen Halbkreis über Strecke AB mit dem
Radius AB/2.
Zeichne die Mittelsenkrechte zur Strecke AB.
 |
...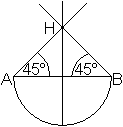 |
Trage den Winkel von 45° an AB in A ab.
Trage den Winkel von 45° an AB in B ab.
Nenne den Schnittpunkt der freien Schenkel H.
 |
...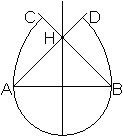 |
Zeichne den Kreisbogen BD um Punkt A mit dem Radius AB.
Zeichne den Kreisbogen AC um Punkt B mit dem Radius AB.
 |
...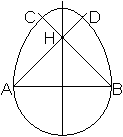 |
Zeichne den Kreisbogen CD um Punkt H mit dem Radius HD. |
...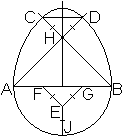 |
Verschiebe das Dreieck DCH vertikal nach unten,
so dass die Seite CD auf AB liegt.
Es gilt somit HD=HC=FE=EG.
Das magische Ei ist fertig.
 |
...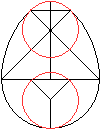 ... ... |
Man kann auch statt des Dreiecks DCH den Berührkreis
betrachten und diesen vertikal nach unten verschieben.
Dann wird deutlich, dass auch EJ zu HD (=HC=FE=EG) kongruent
ist.
 |
...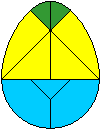 ... ... |
Die Ei-Figur enthält einen Halbkreis, zwei Achtelkreise,
die sich überlappen, und ein Viertelkreis, zerlegt in zwei Achtelkreise.
Die Radien sind r, 2r und, wie im nächsten Kapitel
gezeigt werden wird, [2-sqrt(2)]r.
|
Berechnungen
top
Der Radius des Halbkreises r=AB/2 sei gegeben.
...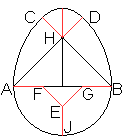 ... ... |
Dann ist
AH=(1/2)sqrt(2)*AB=(1/2)sqrt(2)(2r)=sqrt(2)r
HD=AD-AH=2r-sqrt(2)r=[2-sqrt(2)]r
FG=CD=sqrt(2)*HD=sqrt(2)*[2-sqrt(2)]r=[2sqrt(2)-2]r
AF=[2r-FG]:2=r-FG/2=r-[sqrt(2)-1]r=[2-sqrt(2)]r
EJ=r-FG/2=r-[sqrt(2)-1]r=2r-sqrt(2)r=[2-sqrt(2)]r |
gerundet
AH=1,41r
HD=0,59r
FG=0,83r .
. |
Es fällt auf, dass Seiten der Länge [2-sqrt(2)]r
achtmal auftreten. Sie sind rot markiert.
Der Flächeninhalt der
Ei-Figur ist
A=(1/2)pi*r²+[2*(1/8)pi*(2r)²-r²]+(1/4)pi*[2-sqrt(2)]²r²
= ... =[3*pi-1-sqrt(2)pi]r², angenähert A=3,98r².
Der Umfang der Ei-Figur ist
U=(1/2)[2pi*r]+2*(1/8)*[2pi*(2r)]+(1/4)*[2pi*[2-sqrt(2)]r]
= ... = [3pi-(1/2)pi*sqrt(2)]r, angenähert U=7,20r.
Figuren top
Zahlreiche Vögel findet
man auf der Webseite von Michael Bischoff.

|
Mein Exemplar von der Spielkiste Bethel |
Magisches Ei
im Internet top
Deutsch
Ankerstein GmbH
Anker
Jettes Merkzettel
Das
magische Ei (.pdf-Datei)
Michael Bischoff
Tangram for you
Wikipedia
Ei
des Kolumbus
Englisch
John Rausch
Put-Together
- Egg Of Columbus
Michael Bischoff
Tangram for you
Wikipedia
Egg
of Columbus (tangram puzzle), Egg
of Columbus, Egg
of Columbus (mechanical puzzle)
Referenzen top
(1) Karl-Heinz Koch: ...lege Spiele, Köln 1987 [ISBN
3-7701-2097-3]
(2) Rüdiger Thiele, Konrad Haase: Teufelsspiele,
Leipzig/Jena/Berlin 1991 (Urania-Verlag)
(3) Pieter van Delft, Jack Botermans: Denkspiele der
Welt, München 1998 [ISBN 3-88034-87-0]
(4) Jack Botermans, Jerry Slocum: Geduldspiele der Welt,
Augsburg 2005 [ISBN 3-8289-4949-5]
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2010 Jürgen Köller
top |
 ...
... ...
... ...
... ...
...
 ...
... ...
... ...
...
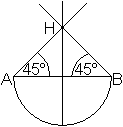



 ...
... ...
... ...
...