|
What is a Magic Hexagon?
The magic square first
... ... ... |
This is certainly well known:
You can distribute the numbers 1 to 9 in a 3x3 square
in such way that the sums vertically, horizontally and diagonally have
the same value. It is 15.
 |
You find more on my page Magic
Square.
...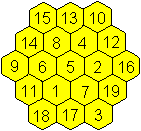 ... ... |
Correspondingly a magic hexagon is a figure, which contains
the numbers 1 to 19 and where the sums horizontally (-), sloping up to
the right (/) and up to the left (\) are equal. It is 38.
There is only one hexagon, too.
 |
Searching
for Magic Hexagons
top
Hexagons of the degree n
The magic hexagon is in a sequence of increasing
hexagons.
...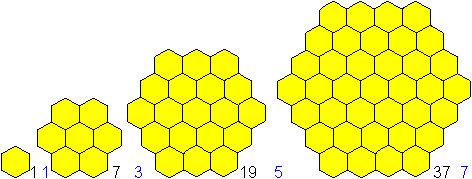 ... ... |
The hexagons have 1,7,19, 37, ... small hexagons.
Generally the hexagon of the order n has 3n²-3n+1
hexagons.
The hexagons have 1,3,5,7,...,
generally
2n-1, rows. |
Derivation
of the term 3n²-3n+1
If you calculate the differences of the numbers 1,7,19,37,...,
you get 6,12,18, ... and then as the difference of the differences 6, 6,
6, ... .
Thus you have a sequence of the form f(n)=an²+bn+c.
n=1 makes1=a+b+c
n=2 makes 7=4a+2b+c
n=3 makes 19=9a+3b+c |
The system of equations has the solution a=3, b= - 3
and c=1.
Thus the n-th term of the sequence is 3n²-3n+1. |
There is 3n²-3n+1=3n(n-1)+1.
This is the idea for the following geometric view.
...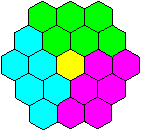 ... ... |
You can divide every hexagon in three parallelograms
with the measurements n and (n-1).
A small hexagon is left.
In the drawing is n=3. |
Searching
for the magic number
There are equal sums in a magic
hexagon. This sum H is called the magic number of the hexagon. If you add
all numbers in a hexagon, you have the sum S=H+H+...+H (z times) or S=zH.
The variable z is the number of parallel rows.
The number of rows is 1, 3, 5, 7, generally z = 2n-1.
According to the sum formula 1+2+3+...+m = m(m+1)/2
you get
S = (3n²-3n+1)[3(n+1)²-3(n+1)+1]/2
= (9n4-18n³+18n²-9n+2)/2.
Then you have H = S/z = S/(2n-1) = (9n4-18n³+18n²-9n+2)/[2(2n-1)]
= (9n4-18n³+18n²-9n+2)/(4n-2).
The magic number, given as a quotient, must be an integer.
You can show by a clever calculation that there is the
only solution n=3.
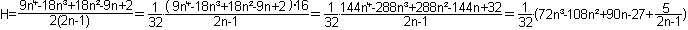
You recognize that H or 32H is only a whole number, if
5/(2n-1) is, too. n=3 is a solution that fits. The numbers n= -2, 1,0 don't
fit.
You can also find this solution by a computer. You replace
n by "all" numbers in the term H=(9n4-18n³+18n²-9n+2)/(4n-2)
and find the integers -2, 1,0, and 3.
Searching
for the places of the 19 numbers
... ... ...
|
You see that, if there is a magic hexagon, it must have
the order 3.
It exists!
It is amazing that there is only one magic hexagon. It
isn't easy to find the distributions of the numbers 1 to 19. The search
is a combination of logic and trial.
You find descriptions at (3), (6), (Torsten Sillke, URL
below).
 |
To
the History of the Magic Hexagon top
Martin Gardner
made this topic popular like he did with many problems lately.
He tells a nice story in book (4).
He heard of the magic hexagon by a letter sent by Clifford
W.Addams, a retired employee at a railway company from Philadelphia. This
man started in working on the hexagon in 1917 and found a solution in 1957
by trial and error. He lost it and found it again in 1962.
Gardner highly regarded the problem, when he put the
mathematician Charles W. Trigg of the university of Los Angeles on it.
He found out that the magic hexagon is unique and obviously unknown in
the mathematical literature.
Trigg published his proof in "Recreational Mathematics"
(3) in 1964. You can read his article at Torsten Sillke (URL below).
The problem was already known
in the end of the 19th century.
You can read at Harvey Heinz (URL below): "Jerry Slocum
mailed me a copy of an advertisement (?) dated 1896, crediting W. Radcliffe,
Isle of Man, U.K. with this discovery in 1895".
Heinrich Hemme published
an article in the magazine Bild der Wissenschaft (1988) and Hans
F. Bauch in Wissenschaft und Fortschritt (1990) that the royal
architect (königlicher Baumeister) Ernst von Haselberg from Stralsund
knew, solved and proved the definiteness of this problem in 1887 (1), (5),
(6).
... ... ... |
This is a decoration wall beside the town hall of Stralsund,
which was renovated during "von Haselberg"'s period of office.
When I visited Stralsund in 1995 I thought it was worth
taking a photo. |
Magic T-Hexagon top
There is another magic hexagon
however formed by triangles. It is called the magic T-hexagon (triangle
hexagon). The hexagon above is called H-hexagon (hexagon hexagon) in difference.
...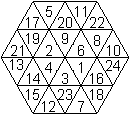 ... ... |
The hexagon is an arrangement of 24
equilateral triangle.
You can distribute the numbers 1 to 24, so that it becomes
magic.
12 sums horizontally (-), sloping up to the right (/)
and up to the left (\) are equal. It is 38.
 |
Number
of the triangles
The magic hexagon is in a sequence of increasing hexagons.
...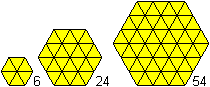 ... ...
|
The hexagon of the order n has 6n² triangles.
 |
Magic
numbers
It is S=zH again.
S = 1+2+3+ ... +6n² = 6n²(6n²+1)/2 = 18n4+3n²
and z = 2n makes
H = S/z = (18n4+3n²)/2n =[3n(6n²+1)]/2
The right hand term H is only then an integer, if the
numerator is even. The consequence is, n must be an even number.
Thus only the middle one of the three hexagons shown
above can be magic.
There are many magic hexagons of this kind.
To the History
of Magic T-Hexagons top
...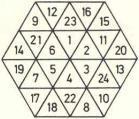 ... ... |
As far as known today the magic T-hexagon was investigated
by Hans F. Bauch for the first time. He published his results in the Mathematischen
Semesterberichten in
1991 (7).
The drawing is an example from the original version,
a T-hexagon with a simple inner hexagon.
 |
The T-hexagon is called "magic hexagon D(4)". D is for Dreieck
(triangle), 4 for the number of rows.
You find the name T-Hexagon on John Baker's web
site (URL below). Obviously John Baker and David King found the T-Hexagons
once more, independent from Hans F. Bauch. You can read on John Baker's
Site: "This arrangement was discovered on 13th September, 2003 and as far
as we can ascertain is the first example of a magic T-hexagon."
Variants
of the Magic Hexagon top
1) Magic hexagon with integers
...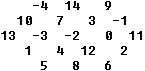 ... ... |
You can find an arrangement of the successive numbers
-4, -3, -2, ..., 13, 14 in a hexagon of the order 3, so that it is
magic.
The magic number is 19. |
...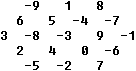 ... ... |
This hexagon contains the numbers -9 to +9
with the magic number 0.
 |
You can probably generalize it: You can find an arrangement
of the numbers -3n(n-1)/2 to +3n(n-1)/2 in a hexagon
of the order 3, so that a magic hexagon with the magic number 0 develops.
(Information by Torsten Sillke, URL below).
There is no proof yet.
You find magic hexagons of
the orders 4, 5 and 7 at en.wikipedia. They have start numbers >1.
Zahray Arsen is the author.
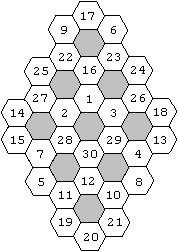
2)
Magic hexagon and a mean
... ... ...
|
The hexagon of the order 3 contains the numbers 1 to
19 like the magic hexagon above.
All the 15 rows don't have the same sum, but the same
mean 10.

|
Origin: Fred W. Helenius ( Torsten Sillke)
3)
Magic star
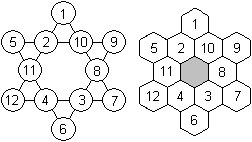
|
It has the numbers 1 to 12.
There are 6 equal sums.
The magic number is 26.
 |
The magic star was known in the 19th
century. There are 96 arrangements in book (2).
You find more on the internet
at "Suzanne Alejandre and Mutsumi Suzuki's Magic Stars" (URL below)
4)
Hexagram
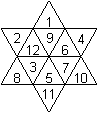
|
It has the numbers 1 to 12.
There are 6 sums with 4 summands.
The magic number is 33.
 |
Found at MathWorld (Bolt, B.; Eggleton, R.; and Gilks,
J. "The Magic Hexagram." Math. Gaz. 75, 141-142, 1991)
5)
First figure of 9 hexagons
...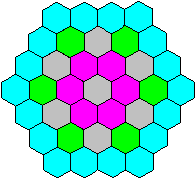 ... ...
|
 ... ...
|
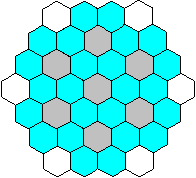
If you take away 7 small hexagons at a hexagon of the
order 4, you get a figure with 3 concentric rings and a chain of 6 hexagons. |
... ... ... |
You can distribute the numbers 1 to 30 in this hexagon
(2 views) in such a way that it becomes magic.
There are 9 equal sums with 6 summands produced by the
numbers in the corners of the small hexagons.
The magic number is 93.
There are many solutions. |
Origin: Harvey Heinz (URL below)
6)
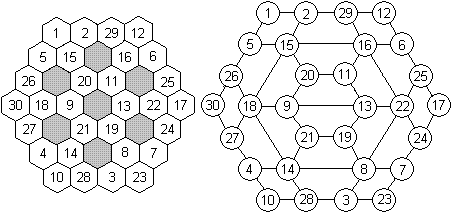
Second figure of 9 hexagons
... ... ... |
There is another arrangement of 9 hexagons, which you
can fill with the numbers 1 to 30, so that it becomes magic.
The figure is formed by 9 rings with common parts.
The magic number is 93. This is the sum of the numbers
of one hexagon.
There are many solutions.
I found an information on Jaewook Shin's site with a picture
as a reference:
"The original source of the problem: Gu-Su-Ryak by Choi,
Seok Jung (1646~1715). This book is displayed in the museum of Daejeon
history in Daejeon, Korea." |
Origin: http://www.mcs.anl.gov/~jaewook/papers/ms_thesis.html
(2006 online)
The
Magic Hexagon on the Internet top
German
Wikipedia
Magisches
Sechseck, Ernst
von Haselberg
English
David King
Hall
of Hexagons
Eric W. Weisstein (World of Mathematics)
Hexagon,
Talisman
Hexagon,
Magic
Hexagon, Magic
Hexagram
Frank R. Kschischang;
The
Magic Hexagon
Hans F Bauch
The
magic hexagon of Ernst v. Haselberg (.pdf-file)
Mutsumi Suzuki (bei mathforum)
Magic
Stars (recommended)
Torsten Sillke
Magic
Hexagon, Magic-Hexagon-Trigg
Wikipedia
Magic
hexagon
References top
(1) Ernst von Haselberg:
Section 795: Zeitschrift für mathematischen
und naturwissenschaftlichen Unterricht 19 (1888) 429
Aufgabe
Section 801: Zeitschrift für mathematischen
und naturwissenschaftlichen Unterricht 20 (1889) 263-264 Auflösung
(2) Hermann Schubert: Mathematische Mußestunden, Neubearbeitung
von F.Fittig, Walter de Gruyter und Co, 1935
(3) Charles W. Trigg: A Unique Magic Hexagon, Recreational Mathematics
Magazine (January-February 1964)
(4) Martin Gardner: Mathematisches Labyrinth, Braunschweig/Wiesbaden
1979 [ISBN 3-528-08402-2]
(5) Heinrich Hemme: Das magische Sechseck, Bild der Wissenschaft (Oktober
1988) 164-166
(6) Hans F. Bauch: Zum magischen Sechseck von Ernst v. Haselberg, Wissenschaft
und Fortschritt 40:9 (1990)
(7) Hans F. Bauch: Magische Figuren in Parketten, Mathematische Semesterberichte
38:1 (1991)
(8) Klaus-Peter Rudolph, Hans Friedrich Bauch: Gurami - das neue Zahlenrätsel,
Berlin 2011 [ISBN 978-3-9811892-3-0]
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
2006 Jürgen Köller
top |
 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...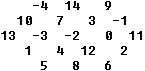 ...
...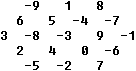 ...
... ...
...

 ...
... ...
... ...
... ...
...