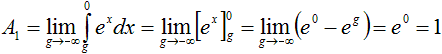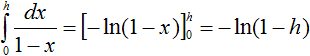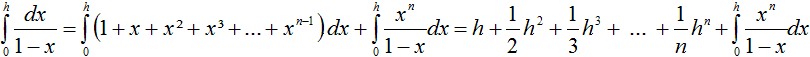|
Was ist die Logarithmusfunktion?
... ... ... |
Die Logarithmusfunktion ist die Umkehrfunktion der Exponentialfunktion
mit f(x)=ax (a>0). D.h., dass in der Darstellung y=ax
die Variablen x und y vertauscht werden: x=ay.
Es wird also bei fester Basis nicht dem Exponenten eine
Potenz zugeordnet, sondern der Potenz ein Exponent. |
Statt der impliziten Darstellung x=ay
führt man die Schreibweise y=loga(x) bzw. g(x)=loga(x)
ein.
Man liest loga(x)
als Logarithmus von x zur Basis a.
Der Logarithmus ist eine Hochzahl.
Beispiele
Die Gleichung 9=3y führt zu y=2 oder
log3(9)=2.
Die Gleichung 3=3y führt zu y=1 oder
log3(3)=1.
Die Gleichung sqrt(3)=3y führt zu y=1/2
oder log3[sqrt(3)]=1/2.
Die Gleichung 1/3=3y führt zu y= -1 oder
log3(1/3)= -1.
Drei Logarithmen top
Von Bedeutung ist die Logarithmusfunktion, wenn die Basis
2, e (eulersche Zahl) oder 10 ist.
Nach ISO 31-11 gibt es für die zugehörigen
Funktionsterme einfachere Schreibweisen, nämlich
log2(x)=lb(x), loge(x)=ln(x)
und log10(x)=lg(x).
lb(x) heißt binärer oder dualer, ln(x) natürlicher
und lg(x) dekadischer Logarithmus.
...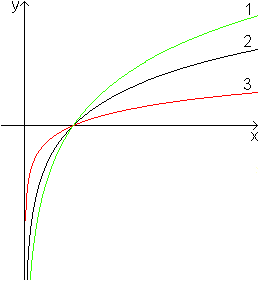 ... ... |
Die Graphen links gehören zu
g1(x) = lb(x), g2(x) = ln(x)
und g3(x) = lg(x).
Beschreibung
>Die Logarithmusfunktion hat bei dem größtmöglichen
Definitionsbereich D=|R+ den Wertebereich W=|R.
>Der Graph ist streng monoton steigend.
>Die y-Achse ist Asymptote.
>Die y-Werte sind für x<1 negativ und für
x>1 positiv.
>Für x gegen Unendlich geht auch y gegen Unendlich. |
Rechengesetze top
Die Potenzgesetze führen zu den Logarithmusgesetzen
(I), (II), (III) und (IV).
(I) log(pq)=log(p)+log(q)
Herleitung
Es sei h=loga(p) oder ah=p und
k=loga(q) oder ak=q.
Dann ist pq = ah * ak=ah+k
.
Die Potenzgleichung ah+k =pq führt zu
loga(pq)=h+k oder loga(pq)=loga(p)+loga(q),
wzbw..
(II) log(p/q)=log(p)-log(q)
Herleitung
Es sei h=loga(p) oder ah=p und
k=loga(q) oder ak=q.
Dann ist p/q = ah / ak=ah-k
.
Die Potenzgleichung ah-k =p/q führt zu
loga(p/q)=h-k oder loga(p/q)=loga(p)-loga(q),
wzbw..
(III) log(xn)=n*log(x)
Herleitung
Es sei h=n*loga(x) oder h/n = loga(x)
oder ah/n=x.
Die Potenzgleichung ah/n =x führt zu
ah = xn oder loga(xn)=h oder
loga(xn)=n*loga(x), wzbw..
(IV) log(x1/n)=(1/n)*log(x)
Herleitung
Es sei h=(1/n)*loga(x) oder hn = loga(x)
oder ahn=x.
Die Potenzgleichung ahn =x führt zu ah
= x1/n oder loga(x1/n)=h oder loga(x1/n)=(1/n)*loga(x),
wzbw..
Basisumrechnung
Es stellt sich z.B. die Frage, welcher Zusammenhang zwischen
den Logarithmen lg(x) und ln(x) besteht.
Behauptung: lg(x)=ln(x)/ln(10)
Beweis:
Es folgt aus y=lg(x) oder y=log10(x) die Potenzgleichung
10y=x.
Dann ist ln(x)/ln(10) = ln(10y)/ln(10)=y*ln(10)/ln(10)=y.
Das heißt aber lg(x) = ln(x)/ln(10), wzbw..
Auf dem gleichen Wege kann
man allgemein zeigen: logb(x) = loga(x)/loga(b).
Ermittlung
der Logarithmen top
Im Allgemeinen sind die Logarithmen transzendente Zahlen,
die angenähert als Dezimalbrüche angegeben werden können.
Diese werden über konvergente Reihen gewonnen, dann aber in beliebiger
Genauigkeit.
Taschenrechner
... ... ... |
Es ist heute keine Schwierigkeit, sich Logarithmen zu
verschaffen. Es gibt Taschenrechner.
Der TI30 z.B. hat dafür die Tasten LOG und LN. |
Mit LOG bestimmt man z.B. lg(2) mit der Tastenfolge 2 LOG
und erhält lg(2)=0.301029996.
Mit LN bestimmt man z.B. ln(2) mit der Tastenfolge 2
LN und erhält ln(2)=0.693147181.
Es ist unsinnig, alle Dezimalen vom Rechner zu übernehmen.
Es genügen wohl vier Dezimalen, so dass gilt: lg(2)=0,3010
und ln(2)=0,6931.
Soll man umgekehrt die Potenz
bestimmen, wenn der Logarithmus gegeben ist, so stehen die Tastenkombinationen
2nd LOG und 2nd LN bereit.
So berechnet man z.B. x=100,3010 durch die
Tastenfolge 0.3010 2nd LOG und erhält x=1.99986187.
So berechnet man z.B. x=e0,6931 durch die
Tastenfolge 0.6931 2nd LN und erhält x=1.999905641.
Gerundet ist das in beiden Fällen 1,9999 oder sinnvoll
gerundet 2.
Logarithmentafel
In Vor-Rechner-Zeiten las man die
Logarithmen (für die Multiplikation von Zahlen) aus Tabellen ab (1).
...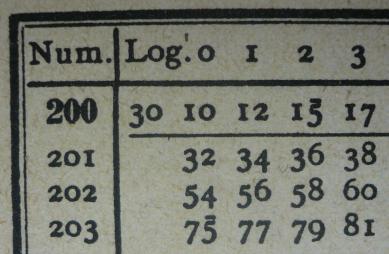 ... ... |
Das ist der Ausschnitt einer Tabelle. Man findet lg(2)=0,3010.
Allerdings liefern die Logarithmentafeln nur die Ziffernfolge. Das Komma
muss man selbst setzen, wie, das zeigen die folgenden Beispiele.
|
lg(2)=0,3010
|
lg(20)=1,3010
|
lg(200)=2,3010
|
|
Wie man sieht, heißt die Zahl x in y=log10(x)
auch Numerus.
Logarithmus
als Rechenhilfe top
Bevor es Rechner gab, erleichterten
dekadische Logarithmen aus Tafeln das Multiplizieren, das Dividieren, das
Potenzieren und das Wurzelziehen, allerdings auf Kosten der Genauigkeit.
Addieren statt
Multiplizieren
Das Vorgehen soll am Produkt 896*271
erklärt
werden.
>Aus dem Tafelwerk liest man ab: lg(896)=2,9523
und lg(271)=2,4330
>Die Summe der Logarithmen ist dann 2,9523+2,4330=5,3853.
>Aus dem Tafelwerk findet man rückwärts 5,3853=lg(242800).
>Ergebnis: 896*271=242800. Das Produkt 896*271=242816
ist auf 4 Stellen genau ermittelt worden.
Die Gleichung lg(896*271)=lg(896)+lg(271)
ist die Erklärung.
Logarithmieren
Sind in einer Gleichung b=ax die Potenz und
Basis gegeben, so berechnet man den Exponenten durch Logarithmieren.
Das heißt, man geht von b=ax zu lg(b)=lg(ax)
oder lg(b)=x*lg(a) und schließlich zu x=lg(b)/log(a) über.
Beispiel
282475249=7x führt zu x=lg(282475249)/lg(7)=8,4510/0,8451=9,93
(Genauer Wert x=10).
Bestimmt man die Logarithmen
z.B. mit dem Taschenrechner TI 30 genauer, so erhält man mit
lg(896)+lg(271) = 8,4509804/0,84509804 = 10 den genauen
Wert.
Multiplizieren
mit dem Rechenstab
Schon bevor es Rechner gab, wurden
die logarithmischen Tafeln durch den Rechenstab ersetzt. Man begnügte
sich mit einer Genauigkeit auf etwa 3 Stellen.
Dieses Multiplizieren soll am Beispiel 121*127 erklärt
werden.

>Man stellt die 1 der Grundskala der Zunge über 1.21
der Grundskala der Körpers.
>Man stellt den Läufer auf 1.27 der Skala der Körpers
ein.
>Man liest darunter die Ziffernfolge ab: 1538. (Die 8
ist unsicher.)
>Durch die Überschlagrechnung 100*100=10.000 ermittelt
man die Größenordnung des Produkts.
>Ergebnis: 121*127=15.380. Das genaue Produkt ist 15367.
Es handelt sich auch hier
um das Addieren von Logarithmen. Man hängt Strecken hintereinander.
Logarithmische Skala
top
Wählt man für der y-Achse eine logarithmische
Skala, wie sie beim Rechenstab auftritt, so werden die Graphen von Exponentialfunktionen
zu Geraden.
...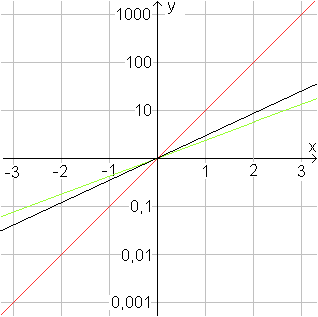 ... ... |
Logarithmiert man die Funktionsgleichung y=10x,
so erhält man lg(y)=lg(2)x oder lg(y)=x.
Trät man lg(y) gegen x auf, so erhält man als
Graphen die erste Winkelhalbierende. Das ist die rote Gerade.
Die Skala der y-Achse heißt logarithmische Skala.
Es gilt z.B. lg(100)=2 und lg(0,01)= -2.
Die schwarze Gerade ergibt sich durch Logarithmieren von
y=ex als lg(y)=lg(e)*x, die grüne Gerade als lg(y)=lg(2)*x. |
...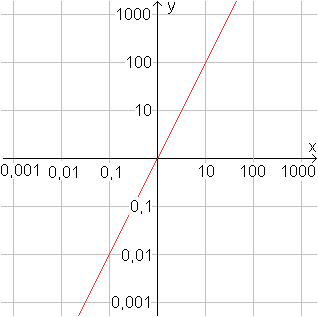 ... ... |
Verwendet man für beide Achsen eine logarithmische
Skala, so stellt sich z.B. die Normalparabel mit p(x)=x2 als
Nullpunktgerade mit der Steigung 2 dar.
Logarithmiert man die Gleichung y=x2 , so erhält
man nämlich lg(y)=2*lg(x).
Der Vorteil dieser Darstellung liegt darin, dass ein weiter
Defintionsbereich und damit auch Wertebereich dargestellt werden kann. |
...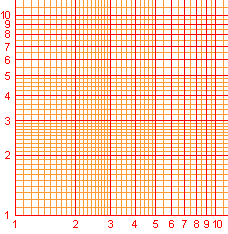 ... ... |
Wegen der Beschriftung der Skalen mit Potenzen von 10
entsteht ein quadratisches Gitter.
Beim doppelt-logarithmischen Papier sieht man, dass bei
einer feineren Einteilung die Abstände nicht gleich sind. |
Ableitung
und Stammfunktion top
Die folgenden Aussagen beziehen sich auf den natürlichen
Logarithmus.
Ableitung
...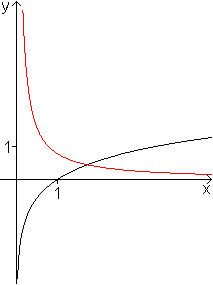 ... ... |
Die Logarithmusfunktion ist als Umkehrfunktion der Exponentialfunktion
differenzierbar.
Behauptung: Die Ableitung der Funktion mit g(x)=ln(x)
ist g'(x)=1/x.
Herleitung
Aus y=ln(x) folgt x=ey.
Für die Ableitung gilt allgemein g'(x)=1/f'(y),
hier also [ln(x)]'=1/(ey)=1/x, wzbw.. |
Stammfunktion
...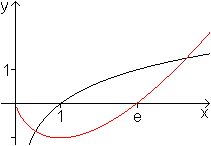 ... ... |
Behauptung: Die Stammfunktion der Logarithmusfunktion
ist G(x)=x*ln(x)-x+C.
Herleitung
Nach der Produktregel gilt [x*ln(x)-x+C]'=ln(x)+x(1/x)-1=ln(x),
wzbw.. |
Deutung
als Flächenstück
...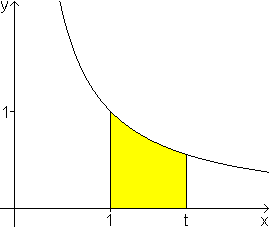 ... ... |
Gegeben sei die Funktion h(x)=1/x.
Dann gilt für das gelbe Flächenstück 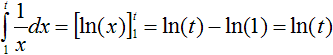 . .
Die Logarithmusfunktion kann also als das Flächenstück,
das von der x-Achse, dem Graphen der Funktion h(x)=1/x und den Vertikalen
x=1 und x=t begrenzt wird, veranschaulicht werden. |
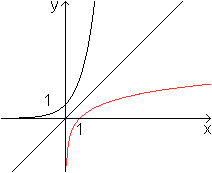
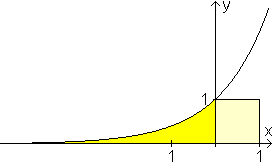
Der Graph der Exponentialfunktion
mit f(x)=ex begrenzt im zweiten Quadranten ein Flächenstück,
das bis ins Unendliche reicht. Trotzdem ist die Fläche endlich, nämlich
1 FE.
... ... ... |
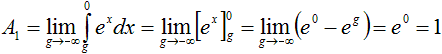 |
Übertragen auf die Umkehrfunktion g(x)=ln(x) heißt
das, dass das im vierten Quadranten eingeschlossene Flächenstück
auch den Flächeninhalt 1 FE hat.
Reihenentwicklungen
top
ln(1+x) und ln(1-x)
Eine bekannte Reihe ist ln(1+x)=x-(1/2)x²+(1/3)x³-
... mit dem Konvergenzbereich -1<x<=1.
Zur Herleitung
Man geht von der folgenden geometrischen
Reihe aus.
1/(1-x)=1+x+x2+x3+
... +xn-1+xn/(1-x)
Dann berechnet man ein Integral
auf zweierlei Weise.
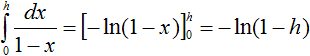 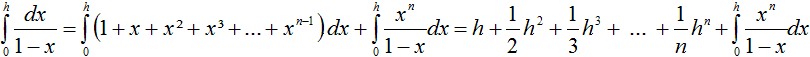
Man kann das Integral ganz rechts
vernachlässigen [(2) Seite 176f.].
Auf diese Abschätzung gehe
ich nicht ein.
Es gilt also ln(1-x)=-x-(1/2)x²-(1/3)x³-
... . Die Reihe ist konvergent für -1<=x<1.
Setzt man in -ln(1-x)=x+(1/2)x²+(1/3)x³+
...den Randwert x=1 ein, so entsteht die Leibniz-Reihe 1+(1/2)+(1/3)+ ...
. Sie ist divergent.
Ersetzt
man x durch -x, so ergibt sich ln(1+x)=x-(1/2)x²+(1/3)x³- ...
.
Die Reihe ist konvergent für
-1<x<=1.
Setzt man in ln(1+x)=x-(1/2)x²+(1/3)x³-
... den Randwert x=1 ein, so ergibt sich ln(2)=1-1/2+1/3-1/4+ ... .
ln(1-x)/ln(1+x)
Oben steht, dass man die Logarithmen
über Reihen berechnen kann. Die beiden Reihen zu
ln(1-x) und ln(1+x) sind weniger gut zur Berechnung geeignet, da sie nur
langsam konvergieren
[(3) Seite 126f. und Zahlenbeispiel
unten].
Aber man kann die beiden Reihen
kombinieren.
Es gilt ln[(1+x)/(1-x)]=2[x+(1/3)x3+(1/5)x5+...].
Zur Herleitung
Für -ln(1-x) schreibt man
ln[1/(1-x)].
Dann addiert man die Reihen ln[1/(1-x)]=x+(1/2)x²+(1/3)x³+
... und ln(1+x)=x-(1/2)x²+(1/3)x³- ... gliedweise und erhält
ln[(1+x)/(1-x)]=2x+(2/3)x3+(2/5)x5+...
=2[x+(1/3)x3+(1/5)x5+...].
Zahlenbeispiel:
> Die Folge zu ln(1+x) ergibt für
x=2 und 4 Summanden ln(2)=1-1/2+1/3-1/4=0,58.
> Die Folge zu ln(1-x)/ln(1+x)
ergibt für x=1/3 und 3 Summanden ln(2)=2[1/3+(1/3)(1/3)3+(1/5)(1/3)5]=0,693004114
oder gerundet 0,693.
> Der Tabellenwert ist ln(2)=0,693147181.
Euler-Mascheroni-Konstante
In diesem Zusammenhang ist die Folge mit (1+1/2+1/3+
... 1/n)-ln(n) bemerkenswert.
Die Folge ist konvergent mit dem
Grenzwert gamma, der Euler-Mascheroni-Konstante. Sie hat die Dezimalbruchdarstellung
gamma=0,5772... .
Quelle: http://mathworld.wolfram.com/Euler-MascheroniConstant.html
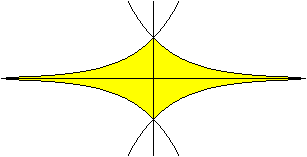
exp(x), exp(-x), -exp(-x), -exp(x)
|
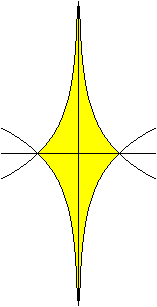
-log(x), -log(-x), log(-x), log(x)
|
Logarithmusfunktion
im Internet top
Deutsch
Jutta Gut
Logarithmen,
Übungen,
Ergebnisse
Wikipedia
Logarithmus,
Dekadischer
Logarithmus, Exponentialfunktion,
Integrallogarithmus,
Harmonische
Reihe, Euler-Mascheroni
Constant
Englisch
Eric W. Weisstein (MathWorld)
Logarithm,
Common
Logarithm,
Natural
Logarithm,
Natural
Logarithm of 2, Cologarithm,
Alternating
Harmonic Series, Harmonic
Series
Juergen Kummer
Draw
Function Graphs
Wikipedia
Logarithm,
Common
logarithm,
Natural
logarithm,
Exponential
function
Referenzen top
(1) F. G. Gauß: Vierstellige logarithmische und
trigonometrische Tafeln, Stuttgart 1953
(2) Lambacher/Schweizer: Analysis, Stuttgart 1954
(3) H.v.Mangoldt / K.Knopp: Einführung in die höhere
Mathematik 2, Leipzig 1957
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2012 Jürgen Köller
top |

 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...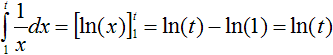 .
.
 ...
...