Leiter-Aufgaben
Inhalt dieser Seite
Was ist eine Leiteraufgabe?
Leiter-Wand-Aufgabe
Leiter-Kiste-Aufgabe
Leiter-Ecke-Aufgabe
Aufgabe von den sich kreuzenden Leitern		 Aufgaben zur rutschenden Leiter
Leitergeschichten
Leiteraufgaben im Internet
Referenzen
.
Zurück zu Hauptseite    "Mathematische Basteleien"

Was ist eine Leiteraufgabe?
Eine Leiteraufgabe ist ein Problem, bei dem eine Leiter eine Rolle spielt. 
Zwei Aufgaben sind Klassiker, nämlich die Leiter-Kiste-Aufgabe (Bild) und die Aufgabe von den sich kreuzenden Leitern. 
Ihr Reiz liegt darin, dass die Fragestellung und der Lösungsansatz einfach sind, die Rechnungen aber schwierig.

Leiter-Wand-Aufgabe top
Die folgende Aufgabe fehlt in kaum einem Schullehrbuch im Zusammenhang mit dem Satz des Pythagoras.
...... 1.Aufgabe
Eine Leiter der Länge c=7 m wird in der Entfernung von d=1,4 m vor einer senkrechten Wand aufgestellt. In welcher Höhe h berührt die Leiter die Wand?
Lösung
Aus c²=h²+d² folgt h=sqrt(c²-d²)=sqrt(7²-1,4²)m=6,9m
Ergebnis: Die Leiter erreicht eine Höhe von 6,9m.

Bei Einführung der Kosinusfunktion wird dann noch der Neigungswinkel bestimmt.
Es gilt cos(alpha)=d/c. Daraus folgt alpha=arc cos (d/c)=arc cos (1,4/7)=78,5°.

Leiter-Kiste-Aufgabe top
Wenn von der Leiteraufgabe die Rede ist, ist meist die folgende Aufgabe gemeint. 
......
 2.Aufgabe:
Eine Kiste in Form eines Würfels der Kantenlänge b=1m steht vor einer Wand. Eine c=5m lange Leiter lehnt an der Wand und berührt dabei die Kiste an einer Kante. Wie hoch reicht die Leiter?

Zwei Lösungen
......
 Offenbar gibt es zwei Möglichkeiten, die Leiter an die Wand zu stellen. 

Damit die Aufgabe nur eine Lösung hat, fragt man bei dieser Aufgabe i.a. nach der "maximalen Höhe". Die Lösung, bei der die Leiter steiler steht, kommt der Wirklichkeit näher.
Formel
...... Es ist nicht günstig die gesuchte Höhe und den Abstand des Fußpunktes der Leiter von der Wand als Variable einzuführen. 

Die Rechnung wird einfacher mit den Teilabschnitten x und y wegen der Symmetrie in den Variablen.
Es gelten zwei Gleichungen: 
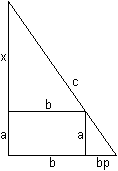
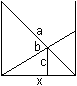
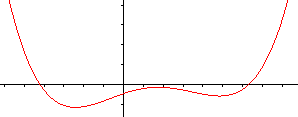
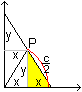
Nach dem Satz des Pythagoras ist (#) c²=(b+x)²+(b+y)². 
Wegen zweier ähnlicher Dreiecke (gelb) ist (##) x:b=b:y oder xy=b². 
Isoliert man y aus (##) und setzt y in (#) ein, so erhält man c²=(b+x)²+(b+b²/x)² oder x4+2bx³+(2b²-c²)x²+2b³x+b4=0.
Das ist eine Gleichung 4.Grades. 
Näherungslösung
In der Aufgabe sind b=1 und c=5. Das führt zur Bestimmungsgleichung x4+2x³-23x²+2x+1=0. 
Man findet eine Näherungslösung, wenn man z.B. den Graphen der Funktion f(x) = (x4+2x³-23x²+2x+1)/64 zeichnet und die Nullstellen bestimmt. Der Faktor 1/64 ist willkürlich gewählt und ermöglicht einen ansehnlichen Graphen.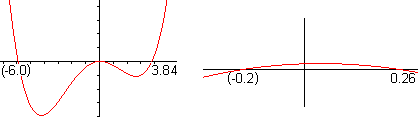
Mit x=0,26 und y=1/x=3,84 ist die Höhe der Leiter 3,84m+1m = 4,84m.
Mit x=3,84 und y=1/x=0,26 ist die Höhe der Leiter 1,26m.
Rechnerische Lösung
Man kommt mit der pq-Formel der quadratischen Gleichungen aus um x4+2x³-23x²+2x+1=0 exakt zu lösen. 
Dazu setzt man in die Gleichung (#) c²=(x+b)²+(y+b)²  c=5 und b=1 und dann y=1/x.
Es ergibt sich (x+1)²+(y+1)²=25 oder (x+1)²+(1/x+1)²=25 oder x²+2x+1+1/x²+2/x +1=25 oder [x²+2+1/x²]+ [2x+2/x]=25. 
Für z=x+1/x ist z²=x²+2+1/x² und 2z=2x+2/x. 
Damit gelangt man zu einer quadratischen Gleichung in z:  z²+2z=25=0. Der weitere Lösungsweg ist:

Ergebnis: Die Leiter erreicht die Höhen 4,84m oder 1,26m.
Variationen
>Man kann nach ganzzahligen Lösungen der Gleichung vierten Grades suchen. 
>Die negativen Lösungen können auch geometrisch gedeutet werden. 
>Man kann an Stelle eines Würfels einen Quader vorgeben.
>Man kann nach dem Verhältnis fragen, in dem die Leiter geteilt wird.
>Man kann den Würfel stauchen:
...... Dann kann man das Leiterproblem auch als Dreiecksaufgabe deuten.
In einem beliebigem Dreieck sind die Seite c, der Winkel gamma und die Winkelhalbierende wgamma gegeben. Gesucht ist die Seite a. 
Für die Leiteraufgabe ist gamma=90°.
Eine Lösung mit Hilfe trigometrischer Formeln, zugesandt von Cavan Orwell 
Noch einmal die Aufgabe:
Gegeben sind eine Leiter der Länge c, die gegen eine Wand lehnt. 
Dabei berührt sie gerade eine Kiste der Kantenlänge b.  Wie hoch reicht die Leiter?
Bei dieser Lösung wird das Augenmerk auf den Winkel t gelenkt. 
Wie oben sind b=1 und c=5. 
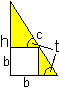
Wegen ähnlicher Dreiecke gilt 5=1/sin(t)+1/cos(t).
Dann ist 5=[sin(t)+cos(t)]/[sin(t)cos(t)] oder 5[sin(t)cos(t)]=sin(t)+cos(t).
Es gilt sin(2t)=2 sin(t)cos(t).
Dann ist 2,5sin(2t)=sin(t)+cos(t).
Quadrieren ergibt 6,25sin²(2t)=[sin(t)+cos(t)]²=sin²(t)+2sin(t)cos(t)+cos²(t)=2sin(t)cos(t)+12 wegen sin²(t)+cos²(t)=1.
So ist 6,25sin²(2t)=sin(2t)+1.
Das ist eine quadratische Gleichung in sin(2t)=y. Es gilt 6,25y²=y+1 oder y²-0,16y-0,16=0.
Sie hat die Lösungen y1=0,08+sqrt(0,1664) und y2=0,08-sqrt(0,1664).
Es gilt y=sin(2t). 
Dann ist sin(2t1)=0,08+sqrt(0,1664) oder 2t1=29,20° oder 2t2=180°-29,2°=150,80°.
Wegen h=c*sin(t) ergibt sich h1=5*sin(t1)=5*sin(14,60°)=1,26 oder h2=5*sin(t2)=5*sin(75,40°)=4,84.
Die Lösung  y2=0,08-sqrt(0,1664) ist negativ und führt nicht zu Winkeln, die von der Leiter angenommen werden können.
Die folgende Lösung sandte mir Hans-Joachim Simon zu.





Mehr über diese Leiteraufgabe findet man in der Homepage von Torsten Sillke (URL unten).
Dort findet man auch die Angabe, dass sich schon Newton mit dem Problem "segment in a corner" beschäftigt hat.
Kent Holing (2) ist der Frage nachgegangen, wann und wo die Aufgabe "Single Ladder Problem" zum ersten Male aufgetaucht ist. "The oldest reference to the square box problem we know is from 1754 (Thomas Simpson: A Treatise of Algebra, John Nourse, Lomndon 1745, page 250). For the general box problem the oldest reference we know is from 1907 (A.Cyril Pearson: The Twentieth Century Standard Puzzle Book, George Routledge&Sons, Ltd., London 1907, page 103)."

Leiter-Ecke-Aufgabe top
...... 3.Aufgabe:
Eine Leiter der Länge c soll einen Flur der Breite b entlang getragen werden. Unglücklicherweise verläuft der Flur am Ende rechtwinklig weiter. Wie lang darf eine Leiter sein, damit sie gerade noch horizontal um die Ecke getragen werden kann?
Das ist eine Extremwertaufgabe. Die Leiterlänge c (bzw. aus rechentechnischen Gründen c²) soll einen größten Wert annehmen. 
......
 Es gilt nach dem Satz des Pythagoras (#) c²=(x+b)²+(y+b)²
Wegen der gelben ähnlichen Dreiecke (##) ist y:b=b:x oder y=b²/x. 
Setzt man y in (#) ein, erhält man die Zielfunktion c²=(x+b)²+(b²/x+b)² oder c²=x²+2bx+b4/x²+2b³/x+2b².
Die erste Ableitung ist (c²)'=2x+2b-2b4/x³-2b³/x². [Die zweite (c²)''Ableitung ist positiv für x>0.] 
Setzt man (c²)'=0, ergibt sich die Gleichung vierten Grades x4+bx³-b³x-b4=0. Man erkennt, dass x=b eine Lösung ist. 
x=b führt zu c/2=sqrt(b) oder zu c=2sqrt(2)b. Diese Lösung wird in der Zeichnung oben dargestellt. 
Ergebnis: Die Leiter ist am kürzesten, wenn c=2sqrt(2)b gilt.

Eine allgemeine Lösung, zugesandt von Johan Asma
Es ist günstig, die Variable p einzuführen, so dass (1+p)b die horizontal liegende Strecke ist. 
Dann gilt  x:(a+x)=b:(b+bp) oder x=ap.

Der Satz des Pythagoras liefert c²=(a+a/p)²+(b+pb)² or c²=a²(1+1/p)²+b²(1+p)²
or c²=a²(1+2/p+1/p²)+b²(1+2p+p²).

Man muss einen Wert für p bestimmen, so dass die Leiterlänge c=c(p) ein Minimum annimmt. 
Dazu benötigt man die Ableitung c'(p) oder einfacher (c²)'=a²(-2/p²-2/p³)+b²(2+2p).
(c²)'=0 führt zu a²(-2/p²-2/p³)+b²(2+2p)=0 or a²(-2p-2)+b²(2p³+2p4) oder -2a²(p+1)+2b²p³(1+p) oder (-2a²+2p³b²)(p+1)=0. 
Die Lösung ist p³=a²/b² or p=(a/b)2/3.

Falls b=a ist wie oben, dann ist p=1 und c²=a²(1+2/p+1/p²)+b²(1+2p+p²)=b²(1+2+1)+b²(1+2+1)=8b² oder c=2sqrt(2)b.

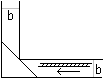
Diese Aufgabe kann auch als Leiter-Kiste-Aufgabe formuliert werden: 
Eine Kiste in Form eines Würfels der Kantenlänge b=1m steht vor einer Wand. Eine Leiter lehnt an sie und berührt dabei die Kiste an einer Kante. Wie lang ist die kürzeste Leiter dieser Art? 

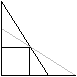
Aufgabe von den sich kreuzenden Leitern       top
Die folgende Aufgabe hat Martin Gardner (1) zur Diskussion gestellt und damit populär gemacht. Wie bei der Leiter-Kiste-Aufgabe ist der Ansatz einfach, die Lösung unerwartet kompliziert.
...... 4.Aufgabe:
Zwischen zwei Hauswänden stehen zwei sich kreuzende Leitern. 
Wie groß ist der Abstand x der Wände, wenn die Leiterlängen a und b und die Höhe c der Kreuzung über dem Erdboden gegeben sind?

Versuch einer Lösung
Es werden die vier Größen h, k, y and z eingeführt (Zeichnung).

Nach dem zweiten Strahlensatz gilt  (#) y:c=x:h und z:c=x:k. Die Produktgleichungen sind yh=cx und zk=cx.
Nach dem Satz des Pythagoras gilt (##) a²=x²+h² und b²=x²+k².
Schließlich ist (###) x=y+z
Man bestimmt aus (##) h und k und setzt sie zuerst in (#) und dann in (###) ein. Es gilt:
Wenn man die Wurzeln beseitigen will, muss man zweimal quadrieren. 
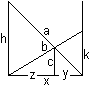
Das führt auf diesem Wege zu einer Gleichung 8. Grades :-(.
Ersatzlösung
Der Abstand der Wände wird nicht direkt bestimmt, sondern über die Höhe h der längeren Leiter.

Aus (#) und (##) folgt 1=c/h+c/k und k=ch/(h-c). 
Aus (##) folgt a²-h²=b²-k². 
Setzt man k=ch/(h-c) in a²-h²=b²-k² ein, ergibt sich nach längerer Rechnung h4-2ch3-(a²-b²)h²+2c(a²-b²)h-c²(a²-b²)=0.

Zahlenbeispiel
...... In einer Skizze werden in eine Schlucht der Breite  x=5 die Leiterlängen a=8,0 und b=7,0 eingezeichnet. Dann ist c=2,8. 
Passend für Leitern sei die Einheit 1m. 

Dann heißt die Gleichung vierten Grades 

h4-5,6h3-15h²+84h-117,6=0.
Zur Gleichung kann die Funktion
f(h)=(h4-5,6h3-15h²+84h-117,6)/256=0
definiert werden. Der zugehörige Graph hat die positive Nullstelle h=6,3. Daraus folgt weiter nach dem Satz des Pythagoras x=4,9.		 ......
Ergebnis: Skizze und Graph liefern etwa die gleichen Ergebnisse.
Ein Reiz dieser Aufgabe besteht nicht unbedingt darin, den Abstand zweier Häuserwände zu berechnen. Die Aufgabe ist in der Unterhaltungsmathematik bekannt geworden, weil es eine Herausforderung ist, Gleichungen mit ganzzahligen Lösungen  und darüber hinaus noch Lösungen mit möglichst kleinen Zahlen für die einzelnen Längen zu finden. In Gardners Buch (1) findet man eine Sammlung. 
Kent Holing (2) hat sich auch mit dieser Leiteraufgabe beschäftigt und ist der Frage nachgegangen, wann die Aufgabe "Crossed Ladders Problem" (CLP) zum ersten Male aufgetaucht ist.
Zitat: "The oldest reference to the CLP we know is from 1894. (Problem 24. The American Mathematical Monthly, 1 (1894), 353-354)"

Aufgaben zur rutschenden Leiter      top
..... Eine Leiter bleibt nur stehen, wenn sie an der Wand und vor allem am Boden haftet.
Es muss Reibung auftreten.

5.Aufgabe:
Welche Kurve beschreibt der Mittelpunkt einer rutschenden Leiter?
......
 P(x|y) sei ein beliebiger Kurvenpunkt.
c sei die :Länge der Leiter.
Ist x=0, so ist y=c/2. - Ist y=0, so ist x=c/2.
Für eine beliebige Lage des Mittelpunktes gilt der Satz des Pythagoras  x²+y²=(c/2)². 
Das ist eine Kreisgleichung. 
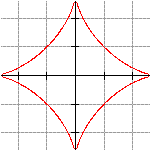
Ergebnis: Der Mittelpunkt der Leiter bewegt sich auf einer Kreislinie.
Es gibt eine praktische Anwendung: Ein Steinsetzer soll einen Halb- oder Viertelkreisbogen pflastern und kann den Bogen aber nicht mit einer Schnur aufreißen, weil im Kreismittelpunkt oder auch davor ein Hindernis (Baum, Wand,...) steht.
(Hinweis von Joachim Grabinski)
Erweiterung
Die Kurve wird zu einer Ellipse, wenn ein beliebiger, aber dann fester Punkt der rutschenden Leiter betrachtet wird. 

Astroide
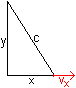
...... Hält man alle Positionen der rutschen Leiter fest, so ergibt sich als Einhüllende eine Astroide.

Rechts die vollständige Astroide mit |x|^(2/3)+|y|^(2/3)=c^(2/3) und c=2.

 ......
Noch einmal: Welche Kurve beschreibt der Mittelpunkt einer rutschenden Leiter?
Robert Jablko teilte mir die folgenden Überlegungen zur Aussage mit, dass sich der Mittelpunkt der Leiter auf einer Kreislinie bewegt.
"Ich habe eine alternative Idee, die ohne Gleichungen auskommt und nur elementargeometrisch argumentiert.
Idee: Umkehrung des Satz von Thales
Die abrutschende Leiter bildet mit der Ecke (E) stets ein rechtwinkliges Dreieck mit gleicher Hypotenuse (Länge der Leiter). Nach Umkehrung des Satzes von Thales befindet sich der Mittelpunkt des Umkreises (M) in einem rechtwinkligen Dreieck immer auf der Mitte der Hypotenuse. Damit wissen wir, dass der Abstand von M und E (Radius des Umkreises) immer gleich groß sein muss, nämlich die halbe Leiterlänge. Dadurch ergibt sich die Kreisbahn mit Radius halbe Leiterlänge."

6.Aufgabe:
Eine c=5m lange Leiter lehnt gegen eine Wand und rutscht. Das untere Leiterende hat eine Geschwindigkeit von vx =0,3m/s, wenn der Fuß der Leiter x=3m von der Wand entfernt ist. Wie groß ist im gleichen Moment die Geschwindigkeit der Leiterspitze an der Wand?
Allgemeine Lösung
...... c sei die Leiterlänge. 
x(t) und y(t) seien die Entfernungen der Leiter-Enden vom Eckpunkt Wand/Boden. Die Abhängigkeit von der Zeit gibt das Anhängsel (t) an.
Dann sind vx =x'(t) und vy =y'(t)die entsprechenden Geschwindigkeiten.
Es gilt [x(t)]²+[y(t)]²=c².
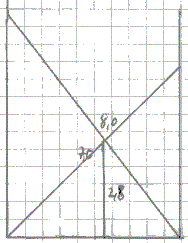
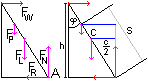
Die Ableitung ist 2x[x'(t)] +2y[y'(t)]=0. Daraus folgt mit y(t) =sqrt{c²-[x(t)]²} die Gleichung y'(t)=-{x[x'(t)]}/sqrt{c²-[x(t)]²}=vy.
Zahlenlösung für c=5m, x=3m und vx =0,3m/s
vy=-3*0,3/sqrt(5²-3²)m/s=-0,23m/s
Ergebnis: Die Leiterspitze bewegt sich mit einer Geschwindigkeit von 0,23 m/s nach unten.
7.Aufgabe: 
Eine homogene Leiter der Länge c=5m und der Masse m=30kg lehnt an einer Wand unter einem Winkel phi=30°. Eine Person der "Masse" M=60kg steigt die Leiter hoch. Wie hoch darf sie steigen, bevor die Leiter gerade rutscht? An der Wand soll keine Haftreibung vorhanden sein, am Boden eine Haftreibung mit der Haftreibungszahl f=1/3. 
Lösung

Kräftebetrachtung:
...... Bei einer Leiter treten die Gewichtskräfte der Person (FP=Mg) und der Leiter (FL=mg) auf. 
Durch den Boden und die Wand entstehen die Normalkräfte FN und FW.
Durch die Reibungskraft FR am Boden wird die Leiter gehalten. 

Kräftebilanz: 
Es gilt im abgeschlossenen System FW=FR und FN=FP+FL.
Bilanz der Drehmomente bezüglich des Drehpunktes A:
(#) FW*c cos(phi)=FP*s sin(phi)+FL*(c/2)*sin(phi)
Weitere Rechnung
Die Leiter beginnt zu rutschen, wenn gerade FR=f FN ist. Daraus folgt, dass in (#) FW durch f(FP+FL) ersetzt werden muss:
f (FP+FL)*c cos(phi)=FP*s sin(phi)+FL*(c/2)*sin(phi)
Die Kräfte ersetzt man durch die Massen über FP=Mg und  FL=mg: 
f(M+m)c*cos(phi)=Ms sin(phi)+m*(c/2)*sin(phi) oder 
(##)   cf(M+m)=Ms tan(phi)+m(c/2)tan(phi) 
Nach s aufgelöst:
Zahlenlösung
Setzt man c=5m, f=1/3, m=30kg, M=60kg und phi=30° ein, ergibt sich s=3,1m.
Ergebnis: Die Person kann 3,1m hoch steigen. 
Die Lösung der folgenden Aufgabe ist in der obigen Rechnung als Sonderfall enthalten.
8.Aufgabe:
Eine homogene Leiter der Länge c=5m und der Masse m=30kg lehnt an einer Wand. An der Wand soll keine Haftreibung sein, wohl aber am Boden mit der Haftreibungszahl f=1/3. Bei welchem Winkel beginnt die Leiter zu rutschen?
Lösung
Man setze in (##) M=0 und erhält fmc=m(c/2)tan(phi). Daraus folgt f=(1/2)tan(phi) oder phi=arc tan(2f).
Zahlenlösung
phi =arc tan(2/3)=33,7°. 
Ergebnis: Der Winkel zwischen der Leiter und der Wand beträgt im Grenzfall 33,7°.

Leitergeschichten top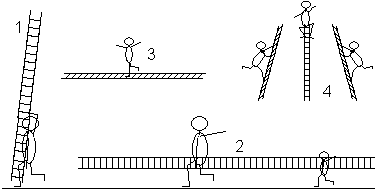

1 Vater trägt eine Leiter.
2 Vater und Sohn tragen eine Leiter.
3 Ein Kind balanciert auf einer Leiter.
4 Ein Zirkusartist steigt auf eine freie Leiter und auf der anderen Seite hinunter. Oben macht er vielleicht einen Handstand oder geht ein Stückchen mit der Leiter.

Alle Vorgänge kann man "verstehen", wenn man Drehmomente betrachtet.

Leiteraufgaben im Internet  top

Deutsch

Bernd R. Mentjes
Das Leiterproblem  (Leiter-Kiste-Aufgabe)

Hans-Jürgen Caspar (bei Mathroids Matheplanet))
Die Leiter und die Sternkurve    (Die Astroide heißt auch Sternkurve) 

Mathematischer Korrespondenzzirkel (Universität Göttingen)
Aufgabe 2   (Leiter-Kiste-Aufgabe)

Matroids Matheplanet Forum Index
Malerarbeit mit Hindernissen
Aufgabe: Malermeister Patzmann hat ein Problem. Er soll einen Saal ausmalen und muss dazu erst eine (möglichst lange) Leiter durch die Kellergänge transportieren. Die Gänge sind rechtwinklig verzweigt und haben quadratischen Querschnitt, 3m breit und 3m hoch. 

René Grothmann
Der Stab, der um die Ecke muss, und einhüllende Kurven

Englisch

Philip Spencer
Classic Fallacies: A Ladder Will Fall Infinitely Fast when Pulled

Eric W. Weisstein (MathWorld)
Crossed Ladders Problem,  Crossed Ladders Theorem,  Moving Ladder Problem

Frank Wolfs
Sample Problem 13-3 (Ladder and Friction)

Jim Wilson
Ladder and Box Problem,  Help with equations

Marek Szapiel (Lawrence S. Husch, visual calculus)
Shortest Ladder over a Fence,  The Longest Ladder

Torsten Sillke
Ladder-Box Problem,  Ladder- move a ladder around a corner,  Hinged Ladder - distance problem

Wikipedia
Crossed ladders problem

Referenzen   top
(1) Martin Gardner: Mathematischer Zirkus, Ullstein Berlin Frankfurt Wien 1988 [USBN 3 550 07692 4]
(2) Kent Holing (Statoil Research Center, Trondheim, Norway): Ladder Problems Revisited (privater Zugang)
(3) Duncan Graham u.a.:A Level Mathematics, Letts Editional London 1995 [ISBN 1 85758 338 8]


Feedback: Emailadresse auf meiner Hauptseite

Diese Seite ist auch in Englisch vorhanden.

URL meiner Homepage:
https://www.mathematische-basteleien.de/

©  2004 Jürgen Köller

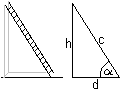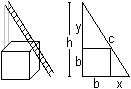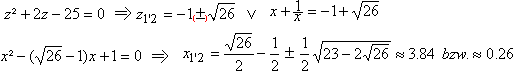
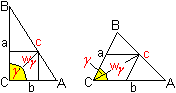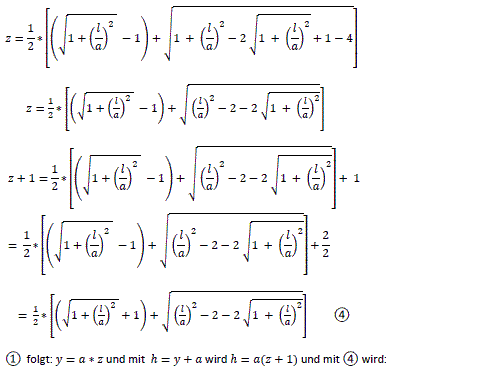
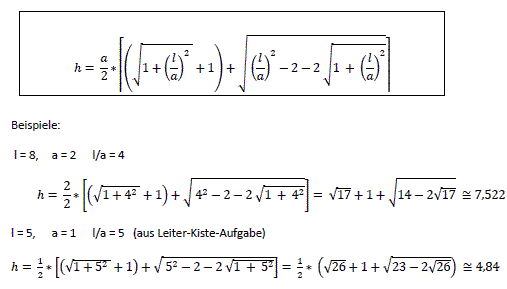
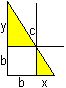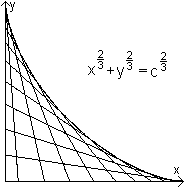top