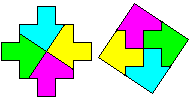Kreuz-Puzzles
Inhalt dieser Webseite
Was sind Kreuz-Puzzles?
Kreuz als geometrische Figur
Neun Kreuz-Puzzles
Lösungen der Kreuz-Puzzles
Kreuze aus Pentominos		 Dreidimensionale Kreuze
Buchstaben zerlegen
Kreuz-Puzzles im Internet
Referenzen
.
Zur Hauptseite    "Mathematische Basteleien"

Was sind Kreuz-Puzzles?
Das wird an einem Beispiel erklärt.
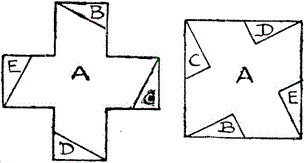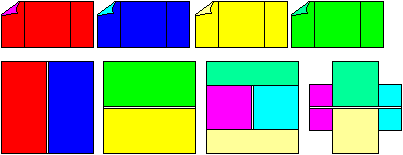
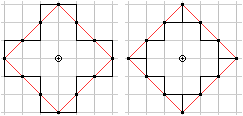
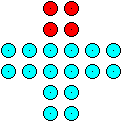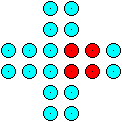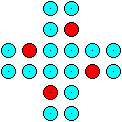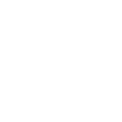
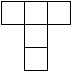
...... Gegeben ist ein griechisches Kreuz. 
Lege durch das Kreuz vier Schnittlinien, so dass man aus den entstehenden Teilstücken ein Quadrat bilden kann.

In diesem einfachen Fall schneidet man vier Ecken ab und füllt die Lücken aus. 

Die Zerlegen des Kreuzes und das Zusammensetzen von z.T. skurrilen Figuren zu einem Kreuz war wohl schon immer eine beliebte Beschäftigung der Unterhaltungsmathematik. Davon zeugen auch einige Kapitel in Dudeneys Werk (s.u.) von 1917. Auf dieser Seite stehen seine Puzzles im Mittelpunkt. Außerdem stelle ich ein 3D-Kreuz aus Pentominos und ein anderes 3D-Kreuz aus "Happy Cube"-Stücken vor.

Kreuz als geometrische Figur      top
 
......
 Auf dieser Seite ist das Kreuz eine Figur mit zwölf gleich langen Seiten, mit acht Innenwinkeln von 90° und vier Innenwinkeln von 270°.

...... Einfacher ist diese Beschreibung.
Es ist eine Figur aus fünf Quadraten. Auf die vier Seiten eines Quadrates wird je ein Quadrat gesetzt. Die vier Quadrate heißen bei einem Kreuz Arme.
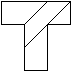
...... Es entsteht auch, wenn man zwei Rechtecke mit dem Seitenverhältnis 1:3 übereinanderlegt, so dass eine symmetrische Figur mit vier Achsen, also eine vierstrahlige Figur, entsteht. 
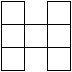
...... Das Kreuz entsteht auch, wenn man ein Quadrat in neun gleiche Quadrate aufteilt und die Quadrate in den Ecken entfernt..............
...... Das Kreuz auf dieser Webseite ist ein spezielles griechisches Kreuz. 
Allgemein hat das griechische Kreuz auch gleich lange Arme und ist vierstrahlig, aber Quadrate kommen nicht zwingend vor.
Größen der Kreuzfigur
Dem Kreuz kann man Größen und Formeln zuordnen. Das ist beim Kreuz einfach. 
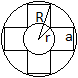...... Gegeben ist die Seitenlänge a. 
Dann ist der Flächeninhalt A = 5a², der Umfang U = 12a, der Radius des Inkreises r = (1/2)sqrt(2)a oder ungefähr 0,74a und der Radius des Umkreises R = (1/2)sqrt(9a²+a²) = (1/2)[sqrt(10)]a oder ungefähr 1,6a.
Unten folgen Puzzles, in denen flächengleiche Quadrate (mit der Seitenlänge x) gesucht werden.
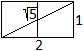... Es gilt die Formel 5a² = x². Aus ihr folgt x = [sqrt(5)]*a.
Da ist es gut zu wissen, dass Wurzel aus 5 die Länge der Diagonalen in einem Doppelquadrat ist.........................
Beim Suchen muss man also das Kreuz so aufteilen, dass 1-2-sqrt(5)-Dreiecke auftreten.

Neun Kreuz-Puzzles top
1
... Zerlege die Figur so in vier gleiche Teile, dass man aus ihnen ein Kreuz bilden kann............................

2
... Zerlege die Figur so in vier gleiche Teile, dass man aus ihnen ein Kreuz bilden kann.........................
3
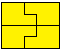... Lege aus den vier Teilen des Rechtecks ein Kreuz..............................................
4
... Lege aus den vier Teilen des Quadrates ein Kreuz................................................................
5
... Lege durch das Kreuz vier gerade Schnitte, so dass man aus den Teilstücken ein Quadrat legen kann.
6
... Lege durch das Kreuz zwei gerade Schnitte, so dass man aus den Teilstücken ein Quadrat legen kann.
7
... Lege durch das Kreuz zwei gerade Schnitte, so dass man aus den Teilstücken zwei Quadrate legen kann. 
8
... Lege aus den vier Teilen ein Quadrat mit einem Kreuz im Inneren......................................................

9
...... Lege aus den acht Teilen des Rechtecks auch ein Hohlkreuz..............................................................
10
...... Zerlege das Kreuz so, dass ein Quadrat mit einem Kreuz im Inneren entsteht. 
Die Ecken des Kreuzes sollen auf je einer Quadratseite liegen..........................................................................................

Lösungen der Kreuz-Puzzles      top
 
1
...

...

 2

3

 

4

5

6

7

 

8

9

10

Kreuze aus Pentominos top
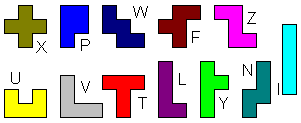...... Die zwölf Figuren aus je fünf Quadraten heißen Pentominos. Die Quadrate muss man so zusammenstellen, dass sie mindestens eine Seite gemeinsam haben. Wegen ihrer mehr oder weniger großen Ähnlichkeit mit großen Buchstaben hat man sie nach ihnen benannt.
Unter den 12 Pentominos befindet sich auch das Kreuz (X). 
Mehr auf meiner Seite Pentominos.

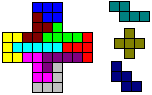...... Es ist eine Herausforderung, aus den Pentominos größere Kreuze zu legen. Die 12 Pentominos haben zusammen 12*5 = 60 Quadrate. Aus ihnen kann man kein ähnliches Kreuz bilden. Nimmt man aber drei Pentominos weg, so ist ein Kreuz mit 3x3-Quadraten möglich. Es hat nämlich 60-3*5 = 45 Quadrate und es ist 45 = 5*9.
Es ist möglich, aus den 12 Pentominos leicht abgeänderte Trost-Kreuze zu entwerfen. Hier sind vier Beispiele. 

8*8-4=60

4*(3*3)+5*5-1=60

4*15=60

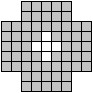
9*9-4*4-5=60
Die Lösungen findet man auf der Webseite von Thimo Rosenkranz (URL unten).

Dreidimensionale Kreuze       top
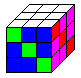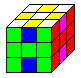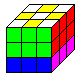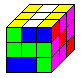
Die drei folgenden Körper kann man als dreidimensionale Kreuze bezeichnen.

Die Bilder wurden mit Hilfe der App "Think 3D Free" von Paul Hangas erstellt.  (URL unten)
Dreidimensionales Kreuz aus Pentominos
............ Pentominos sind meist nicht zweidimensional, sondern sie werden aus Würfeln hergestellt und bilden dann ebene Pentawürfel. Sie sind dann handlicher und ermöglichen Raum-Puzzles.
...... ...... So kann man die fünf Quadrate des Kreuzes in 2x2-Teilquadrate aufteilen und dann zu einem Würfelkörper mit drei Schichten übergehen. Es gilt 3*(5*4) = 60. Somit ist es (nach der Theorie) möglich, aus allen Pentominos diesen Körper zu legen.
Man hat mit Computerhilfe festgestellt, dass es für drei Pentominos keine Lösung gibt, ausgerechnet auch für X nicht. 
Das Pentomino T hat z.B. eine Lösung. 
...
Man kann aus den Pentominos neue Körper bauen. Es folgt ein Kreuz mit kurzen Armen und einem Loch.
...
3D-Würfel aus "Happy Cube"-Stücken
Das Puzzle "Happy Cube" besteht aus 6 Matten aus dickem, weichem Schaumstoff. Jede Matte enthält, von einem Rahmen umgeben, sechs Stücke in der Form von 5x5-Quadraten. Es ist möglich, aus sechs Stücken einen 5x5x5-Würfel zusammenzusetzen. Man kann aber auch kompliziertere Körper bauen wie z.B. einen 3D-Würfel. Der Bauplan steht auf meiner Webseite Happy Cube.

Kreuze auf meiner Homepage

Solitär

Quadrat legen

Zauberwürfel

Game of Life


Magische Karte

Taxi-Geometrie

Figuren in einer Figur zählen

Buchstaben zerlegen     top
Man kann das Kreuz auch als den Buchstaben x ansehen, der aus Quadraten gebildet wird.
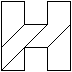
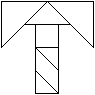
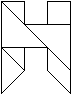
In diesem Zusammenhang sind Puzzles beliebt, die durch Zerschneiden von Buchstaben wie T und H entstehen. Dabei wird Wert darauf gelegt. dass die Teilstücke einfach sind und dass bei Ihrer Ansicht nicht auf den Buchstaben geschlossen werden kann.

Es ist eine Herausforderung, aus Tangramsteinen Buchstaben zu legen.

Kreuz-Puzzles im Internet      top

Deutsch

Martin Scheufens  (Rätsel der Woche, Spiegel)
Ein Kreuz muss dran glauben

Thimo Rosenkranz
Pentomino-2D-Figuren-Übersicht

Wikipedia
Griechisches Kreuz

Englisch

Eric W. Weisstein (MathWorld)
Greek Cross 

Alexander Bogomolny  (cut-the-knot)
Between a Cross and a Square

David Butler
Quarter-the-cross

justpuzzles
Dissections – the Greek cross
Dissections – the Greek cross (2)

Mr Puzzle
Aluminium Cross take apart puzzle

National Centre for Excellence in the Teaching of Mathematics (NCETM)
Focus on...Dudeney’s Greek cross dissection puzzles

NN
Squaring a cross

NN
Crosses and stars

Paul Hangas
Think 3D Free

Theobald, Gavin and Weisstein, Eric W.  (MathWorld)
Dissection

Wikipedia
Cross

Wikimedia Commons
Sangaku of Konnoh Hachimangu 1859   (mittlere Figur)

Yan Kow Cheong (singaporemathplus)
The Mathematics of the Cross

Französisch

La croix de Nob yoshigahara

Referenzen   top
Sam Loyd, Martin Gardner: Noch mehr mathematische Rätsel und Spiele, Köln 1979 [ISBN 3-8321-1145-x] 
HENRY ERNEST DUDENEY: AMUSEMENTS IN MATHEMATICS 1917 bei Gutenberg

Feedback: Emailadresse auf meiner Hauptseite

URL meiner Homepage:
https://www.mathematische-basteleien.de/

©  2017 Jürgen Köller

top
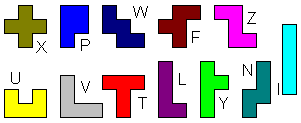