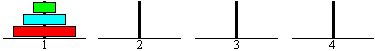|
Was ist der Turm von Hanoi?
Der Turm von Hanoi ist ein klassisches Knobelspiel.
... ... ... |
In seiner einfachsten Form besteht der Turm aus drei
Kreisscheiben, die ein Loch haben und auf einen Pfosten gesteckt werden.
Die Form erinnert an Pagoden. Das sind vielstöckige
Tempeltürme im fernen Osten. So ist der Name zu erklären. |
Er heißt auch der Turm des Brahmanen. Er und eine Geschichte
dazu wurden 1883 von Édouard Lucas erfunden.
Zum Turm von Hanoi gehören noch
zwei freie Pfosten.
...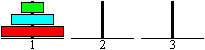 ... ...
|
Der Turm steht zu Beginn auf Platz 1.
Man soll ihn auf Platz 2 neu aufbauen. |
... ... ...
|
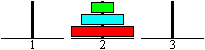
Dabei sind zwei Regeln zu beachten:
(I) Man darf immer nur eine Scheibe umlegen.
(II) Man darf eine größere nicht auf eine
kleinere Scheibe legen.
Der Pfosten auf Platz 3 dient als zusätzliches Zwischenlager.
Lösung
top
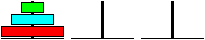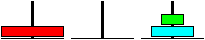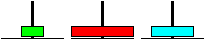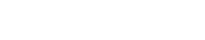
Notation der sieben Züge: 1-2, 1-3, 2-3, 1-2, 3-1,
3-2 und 1-2. - Es genügt die Platzwechsel festzuhalten.
Dieses ist auch der kürzeste Lösungsweg. Er
besteht aus 7=2³-1=2^3-1 Zügen.
Zur Strategie:
Man beachte die kleine grüne Scheibe: Sie wandert
von Platz 1 nach 2, nach 3, zurück nach 1 und nach 2. Die Zahlen 1,2,3
werden zyklisch durchlaufen. Diese Wanderung hilft bei einer Lösung.
Der Turm aus
n Scheiben top
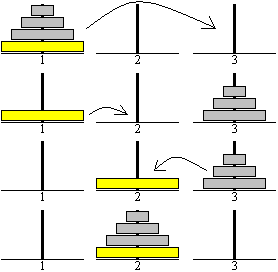
Soll man einen Turm mit vier Scheiben
umsetzen, so führt man diesen Vorgang auf das Drei-Scheiben-Problem
zurück. Man setzt in sieben Schritten den Dreierturm von 1 nach 3,
legt die gelbe Scheibe in die Mitte und baut in wiederum sieben Schritten
den Turm von 3 auf die gelbe Scheibe auf Platz 2 auf.
Man benötigt mindestens 2x7+1=15=2^4-1
Schritte:
 Man kann schrittweise weitergehen:
Man kann schrittweise weitergehen:
Für den 5-Scheiben-Turm braucht man mindestens 2x15+1=31=2^5-1
Schritte,
für den 6-Scheiben-Turm mindestens 2x31+1=63=2^6-1
Schritte.
Verallgemeinerung:
Sind n Scheiben vorgegeben, so braucht man mindestens
2^n-1 Schritte.
Das Problem ist in dieser Aufbereitung beliebt, um den
Unterschied zwischen rekursiver Darstellung [(x(1)=1 und x(n+1)=2x(n)+1]
und expliziter Darstellung [x(n)=2^n-1] einer Folge zu demonstrieren.
Der
Turm von Hanoi mit vier Pfosten top
Wie bei vielen Puzzles sind Abänderungen interessant
und werfen neue Probleme auf.
Oben standen drei Pfosten zur Verfügung. Man kann
in mindestens 7 Schritten den Turm auf einem freien Pfosten neu aufbauen.
Steht ein vierter Pfosten zur Verfügung, so kommt
man mit 5 Zügen aus.
Anfangsstellung:
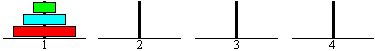
Endstellung:

Die Züge heißen 1-3, 1-4, 1-2, 4-2 und 3-2.
Tabelle für n Scheiben (n=2, 3, 4, 5,...)
|
Anzahl der Züge bei 3 Pfosten
|
03, 07, 15, 31, 63,...
|
Sloane A0002256
|
|
Anzahl der Züge bei 4 Pfosten
|
03, 05, 09, 13, 17,...
|
Sloane A007664
|
Gibt man vier Pfosten statt 3 vor, so verringert sich
die Mindestzahl der Züge.
Bau des Turms
von Hanoi top
1.Version:
Wenn man auf das Äußere des Spiels keinen
Wert legt und mehr an dem logischen Problem interessiert ist, genügen
einfache Pappquadrate unterschiedlicher Größe oder nummerierte
Karten wie die von "Elfer raus" zum Spielen.
2.Version:
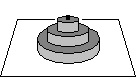
Man kann den Turm von Hanoi wie in der folgendem Bild
herstellen. Die Version mit vier Pfosten ist etwas Besonderes.
 Es ist angebracht mehr Kreisscheiben als im Bild anzufertigen.
Es ist angebracht mehr Kreisscheiben als im Bild anzufertigen.
3.Version:
Im Allgemeinen stehen die Pfosten in einer geraden Linie.
Die drei Pfosten können auch ein gleichseitiges Dreieck bilden. Dann
wird deutlich, dass die größte Scheibe nur einmal gelegt werden
kann. Das Spielfeld hat die Form eines Kleeblatts.
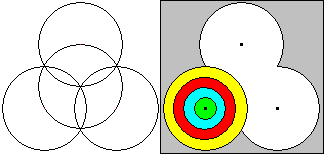 Die Maße sind frei wählbar. Eine genaue Beschreibung
findet man in Buch 2.
Die Maße sind frei wählbar. Eine genaue Beschreibung
findet man in Buch 2.
Mersenne-Zahlen
top
Die Zahlen 2^n-1 heißen Mersenne-Zahlen. Sie waren
von Interesse, da man glaubte, in ihnen eine unendliche Folge von Primzahlen
gefunden zu haben. Diese Frage ist nicht entschieden.
Mersenne-Zahlen sind auch heute noch wichtig, weil man
unter ihnen die größten Primzahlen findet.
Für n=2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127
ergeben sich Primzahlen.
2^127-1 war bis 1952 die größte mit Ziffern
bekannte Primzahl.
Sie hat 39 Stellen und heißt 170141183460469231731687303715884105727.
Den Beweis erbrachte Edouard Lucas.
Danach hat man mit Computerhilfe einige kleinere und vor
allem immer größere mersennesche Primzahlen gefunden.
Die Ergebnisse seit 1999 sind:
Nr.38
Nr.39
Nr.40
Nr.41
Nr.42
Nr.43
Nr.44
Nr.45
Nr.46
Nr.47
Nr.48 |
2^06.972.593 - 1
2^13.466.917 - 1
2^20.996.011 - 1
2^24.036.583 - 1
2^25.964.951 - 1
2^30.402.457 - 1
2^32.582.657 - 1
2^37.156.667 - 1
2^42.643.801 - 1
2^43.112.609 - 1
2^ 57.885.161- 1 |
2.098.960 Stellen
4.053.946 Stellen
6.320.430 Stellen
7.235.733 Stellen
7.816.230 Stellen
9.152.052 Stellen
9.808.358 Stellen
11.185.272 Stellen
12.837.064 Stellen
12.978.189 Stellen
17.425.170 Stellen |
1999
1999
2003
2004
2005
2005
2006
2008
2009
2008
2013 |
Quelle: http://www.mersenne.org/prime.htm
Zur Geschichte
top
Der französische Mathematiker Édouard Lucas
(1842-1891) erfand dieses Spiel und verkaufte es als Spielzeug erstmals
im Jahre 1883.
Zu diesem Spielzeug dachte sich Lucas eine Geschichte
aus, die man im Internet nachlesen kann. Hindupriester sollten auf Geheiß
ihres Gottes Brahma 64 Scheiben umlegen. Dazu benötigten sie theoretisch
mindestens 2^64-1 = 1.8*10 ^19 Züge. Wird in jeder Sekunde eine Scheibe
umgelegt, so dauert das 580 000 000 000 Jahre (!).
Der Turm
von Hanoi im Internet top
Deutsch
Bernhard Berchtold (mathematik.ch)
Hanoi
mit Grafik
Wolfgang Appell (Mathe-Zaubergarten mit Spaß)
Der
Turm von Hanoi
Wikipedia
Türme
von Hanoi, Mersenne-Zahl
Englisch
David E. Wilkins
The
Tower of Hanoi Problem
Eric W. Weisstein (MathWorld)
Tower
of Hanoi
Jaap Scherphuis
Tower
of Hanoi
Miroslav Kolar
Tower of Hanoi
(TH) Puzzle
Neil J. A. Sloane
A183111 Magnetic
Tower of Hanoi
Wikipedia
Tower
of Hanoi
Referenzen
top
(1) Martin Gardner, Mathematical Puzzles & Diversions,
New York 1959
(2) Pieter van Delft /Jack Botermans: Denkspiele der
Welt, München 1980 (1998 neu aufgelegt)
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2002 Jürgen Köller
top |



 ...
... ...
... ...
...