|
Dreiteilung eines Winkels
|
Was ist die Dreiteilung eines Winkels?
... ... ... |
Das Problem der Teilung eines Winkels in drei gleich
große Teilwinkel gehört zu den bekannten Problemen der antiken
Mathematik, wenn man noch hinzufügt ...zu ermitteln allein
mit Zirkel und Lineal.
Es ist gelöst in der Weise, dass die Dreiteilung
unmöglich ist. |
Man bezeichnet das Zeichnen
mit Zirkel und Lineal als Konstruieren. Es geht also um die Konstruktion
der Dreiteilung.
Dazu findet man auf dieser
Seite einige Überlegungen.
Außerdem werde ich, das ist naheliegend, am Ende
auf die Dreiteilung von Figuren und Körpern eingehen.
Teilung des
rechten Winkels
top
... ... ... |
Wenn oben steht, dass die Dreiteilung eines Winkels unmöglich
ist, so ist der allgemeine Winkel gemeint. Es gibt Sonderfälle, für
die es Konstruktionen gibt.
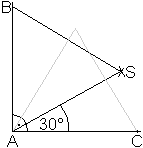
Man denke nur an den rechten Winkel von 90°. Man konstruiert
einen Winkel von 30°, indem man über der Strecke AB ein gleichseitiges
Dreieck errichtet.
Errichtet man über AC ein gleichseitiges Dreieck,
erhält man die andere "Winkelteilende". |
Unmöglichkeitsnachweis
top
Zeichnung
Der Nachweis, dass eine Konstruktion nicht möglich
ist, erfolgt über die Berechnung einer Strecke.
Quelle: (1) Seite 5
...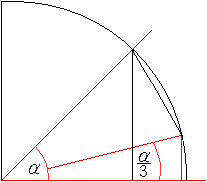 |
Grundlage für die Rechnung ist die nebenstehende
Figur. |
...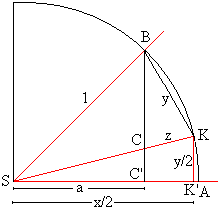 |
Die Figur wird beschriftet.
Der gegebene Winkel sei BSA. Er wird durch die Strecke
a bestimmt, cos(alpha)=a.
SK drittelt den Winkel. Der gesuchte Drittelwinkel wird
durch die Strecke x/2 bestimmt, cos(alpha/3)=x/2.
|
Rechnung
Die Dreiecke SKB und BCK sind ähnlich:
>Sie haben den Winkel SKB gemeinsam.
>Das rote Dreieck SK'K ist dem halben Dreieck von SKB
kongruent. Es gilt Winkel SKK' gleich Winkel SBK.
Als Wechselwinkel an Parallelen sind die Winkel K'KS,
Winkel BCK gleich.
Also sind die Dreiecke SKB und BCK gleichschenklig.
Gleichschenklige Dreiecke mit einem gleichen Winkel sind
ähnlich.
Es gilt dann z:y=y:1 oder
(I) z=y².
>Es gilt der erste Strahlensatz: SC:SK=SC':SK' oder (II)
(1-z):1=a:(x/2).
>Es gilt nach dem Satz des Pythagoras im Dreieck SKK':
(III) (x/2)²+(y/2)²=1.
Das sind drei Gleichungen in der Variablen x, y und z,
aus denen x bestimmt werden soll.
(I) z=y²
(II) (1-z):1=a:(x/2) ergibt 1-z=2a/x oder z=1-2a/x
Daraus folgt y²=1-2a/x.
(III) (x/2)²+(y/2)²=1 führt zu y²=4-x²
Die Variable y wird eliminiert. Das ergibt 1-2a/x=4-x²
oder x³-3x-2a=0.
Sonderfall
Ist a=0, so wird aus der Gleichung x³-3x-2a=0
die einfache Gleichung x³-3x=0 mit den Lösungen x1=0,
x2=+sqrt(3) und x2=-sqrt(3).
Von Interesse ist x2=+sqrt(3). Dann ist cos(alpha/3)=x2/2
oder cos(alpha/3)=+sqrt(3)/2 oder alpha/3=30°.
Das passt zu a=0. Denn nach der Zeichnung ist für
a=0 der Winkel alpha=90°.
Ergebnis
Für beliebige Variable a ist x die Lösung einer
kubischen Gleichung x³-3x-2a=0, also eine Wurzel dritten Grades.
Dann kann x und damit alpha/3 nicht durch eine Konstruktion
gefunden werden.
Das kann man einsehen, wenn man bedenkt, dass beim Konstruieren
nur Geraden und Kreise und ihre Schnittpunkte ermittelt werden und dass
dahinter lineare und quadratische Gleichungen stehen, die nie zu dritten
Wurzeln führen, sondern zu quadratischen.
Konstruierbare
Dreiteilungen
top
Welche Winkel kann man mit Zirkel und Lineal in drei
gleiche Teilwinkel zerlegen?
Dazu sollte man sich zunächst einmal eine Übersicht
über die konstruierbaren Winkel verschaffen.
>Der rechte Winkel 90° wurde schon oben genannt.
>Das gleichseitige Dreieck liefert den Winkel 60°.
>Das Fünfeck ist konstruierbar und hat das Grunddreieck
54°-72°-54°.
Von diesen vier Winkeln aus gelangt man zu weiteren,
denn das Halbieren, das Verdoppeln, das Addieren und Subtrahieren
kann durch Konstruktionen erreicht werden.
Ausgangswinkel sind also
90°, 60°, 54° und 72°.
Halbiert man den Winkel von 72° zweimal, gelangt
man zu 18°.
Halbiert man den Winkel von 60° zweimal, gelangt
man zu 15°.
Der Differenz 18°-15°=3° ist also ein Winkel,
der konstruiert werden kann, damit auch alle Vielfachen des Winkels von
3°. Das sind die Winkel 3°, 6°, 9°, ..., 87°, 90°.
Bildet man die Winkel mit
dreifacher Winkelgröße, gelangt man zu Winkeln, die man dreiteilen
kann. Das sind die Winkel 9°, 18°, 27°, 36°, 45°, 54°,
63°, 72°, 81° und wie gehabt 90°.
Damit wird nicht behauptet, dass dieses alle Winkel sind.
Es gibt unendlich viele.
Zu einem Winkel gibt es eine
Strecke, die ihn charakterisiert. Sie ist z.B. in einem rechtwinkligen
Dreieck die Gegenkathete, wenn die Hypotenuse gleich 1 ist. Das führt
zur Sinusfunktion.
Der folgende Term zu 3° steht auf der Wikipedia-Seite
Exact
trigonometric constants.
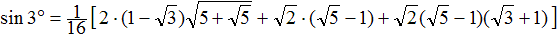 Wie oben gesagt, schlägt sich die Konstruierbarkeit
in einem quadratischen Term nieder.
Wie oben gesagt, schlägt sich die Konstruierbarkeit
in einem quadratischen Term nieder.
Näherungskonstruktion
für kleine Winkel top
...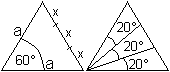 ... ... |
Teilt man die dem 60°-Winkel gegenüberliegende
Seite in drei gleiche Teile und verbindet die Teilpunkte mit dem Scheitel
des Winkels, so entstehen drei Winkel von etwa 20°, wie man durch Nachmessen
bestätigen kann. |
Offenbar kann man die Methode auf beliebige Winkel erweitern,
indem man vom Scheitelpunkt aus auf den Schenkeln zwei gleiche Strecken
abträgt und die Verbindungslinie der Endpunkte wieder in drei gleiche
Teile teilt.
Diese Methode führt
nicht zu einer genauen Drittelung eines Winkels.
...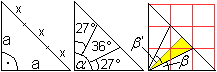 ... ... |
Das zeigt die Teilung des rechten Winkels. Durch Nachmessen
stellt man fest, dass die Winkel von 30° weit entfernt sind.
- Legt man auf die Figur ein Gitter, so kann man tan(beta)=1/2 und tan(beta'/2)=1/3
ablesen. Das führt zu den Winkeln beta=26,6° und beta'=36,9°. |
Auskunft über die Genauigkeit
gibt die folgende mit Computerhilfe erstellte Tabelle.
alpha
alpha/3
beta
Abweichung |
10°
3,3°
3,3°
0,1% |
20°
6,7°
6,6°
0,3% |
30°
10°
9,9°
0,5% |
40°
13,3°
13,1°
1,9% |
50°
16,7°
16,2°
3,0% |
60°
20°
19,1°
4,5% |
70°
23,3°
21,9°
6,3% |
80°
26,7°
24,4°
8,6% |
90°
30°
26,6°
11,5% |
...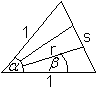 ... ... |
Die zugehörige Rechnung geht zweimal vom Kosinussatz
und vom Sinussatz aus.
> s²=2-2cos(alpha)
>r²=1+(s/3)²-(2/3)s*cos[(pi-alpha)/2]
>sin(beta)
:
sin[(pi-alpha)/2] = (s/3) :
r |
Ergebnis: Diese einfache
Methode wird umso genauer, je kleiner der zu teilende Winkel ist.
Variation
...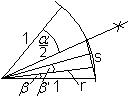 ... ... |
Nach einer Idee von Hugo Steinhaus (3, Seite 264) kann
man dieses Verfahren verfeinern. Man halbiert zuerst den gegebenen Winkel
und teilt den halben Winkel wie oben in drei Teile. Der Winkel beta+beta'
ist angenähert alpha/3. - Die Raffinesse liegt darin, dass der Teilwinkel
beta etwas kleiner und beta' etwas größer als (alpha/2)/3 sind.
So ist diese Methode genauer als die von oben. |
Die Methode
des Archimedes
top
Figur
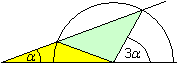 ... ... |
In der Figur aus zwei gleichschenkligen Dreiecken und
einem Halbkreis treten die Winkel alpha und 3*alpha auf.
Sie dient dazu, einen Winkel zu dritteln. |
Beweis
der Winkelbeziehung
...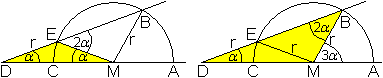 ... ... |
Die beiden Dreiecke DME und BEM sind gleichschenklig,
da die Schenkel gleich dem Radius des Halbkreises sind.
Da der Außenwinkel gleich der Summe der nicht anliegenden
Innenwinkel in einem Dreiecks ist, ergeben sich im linken Dreieck 2*alpha
und weiter im rechten Dreieck 3*alpha als Außenwinkel. |
Zeichnung
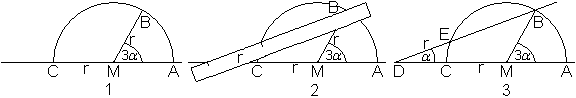 1 Zeichne den gegeben Winkel 3*alpha und einen Kreis um den
Scheitelpunkt mit einem beliebigen Radius.
1 Zeichne den gegeben Winkel 3*alpha und einen Kreis um den
Scheitelpunkt mit einem beliebigen Radius.
2 Markiere auf einem Papierstreifen eine Strecke der
Länge r und passe r zwischen Horizontaler und Kreis außen so
ein, dass die Kante des Streifens auch durch B verläuft.
3 Der Winkel MDB ist der gesuchte Winkel alpha/3.
Ergebnis
Da als Hilfsmittel ein präparierter Papierstreifen
verwendet wird, ist die Zeichnung zwar exakt, aber keine Konstruktion.
Halbkreisgerät
top
Statt des Papierstreifens steht auch eine Kuriosität,
das Halbkreisgerät ("Tomahawk"), zur Verfügung.
...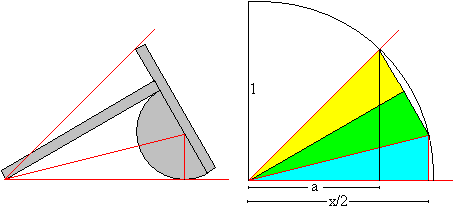 ... ... |
Die Funktionsweise erklärt sich aus der Zeichnung.
Man passt das Gerät im Winkel ein und zeichnet eine
Halbgerade entlang des Lineals.
Dann dreht man es um und erhält eine zweite Halbgerade.
Die Halbgeraden dritteln den Winkel.
|
Weitere klassische
Probleme
top
Die Dreiteilung eines Winkels gehört zu den antiken
Problemen, von denen man weiß, dass sie nicht lösbar sind.
Ich gehe auf andere an anderen Stellen meiner Homepage
ein.
>Die Dreiteilung des Winkels
>Die
Verdoppelung des Würfels
>Die
Quadratur des Kreises
Man könnte noch die Konstruktion vieler regelmäßiger
Vielecke hinzufügen.
Liest ein mathematisch Interessierter
von den Unmöglichkeiten der Konstruktionen, so ist es für ihn
verführerisch, es studierten Mathematikern zu zeigen, dass es doch
geht. Nach etlichen Kontakten in den zehn Jahren meiner Internetpräsenz
habe ich erfahren müssen, dass es sie gibt und dass man nichts ausrichten
kann.
Dreiteilung von
Figuren top
Damit ist nicht gemeint, dass die
Teilfiguren unbedingt kongruent sein müssen. Es reicht die Flächengleichheit.
Strecke
...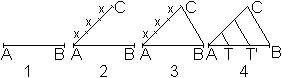 |
1 Die gegebene Strecke sei AB.
2 Trage auf einer Geraden durch A dreimal die beliebige
Strecke x ab. Du erhältst C.
3 Verbinde C mit B.
4 Zeichne durch die Teilpunkte auf AC die Parallelen
zu BC.
Du erhältst die Teilpunkte T und T', die die Strecke
AB dritteln. |
Die Begründung liegt im ersten Strahlensatz.
Quadrat
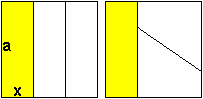
x=(1/3)a
|
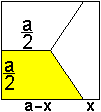
x=(1/6)a
|
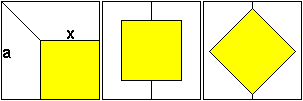
x=(1/3)sqrt(3)a
|

x=(1/6)a
|
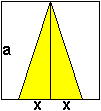
x = (1/3)a
|
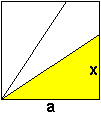
x = (2/3)a
|
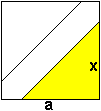
x = (1/3)sqrt(6)a
|

x:y:a = sqrt(6) : sqrt(3) : 3
|
Kreis

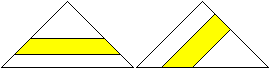
Gleichseitiges
Dreieck
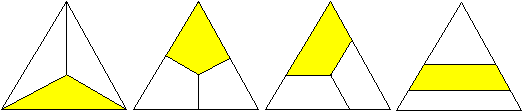
Gleichschenkliges
Trapez, Sechseck, 45-90-45-Dreieck
Die Figuren haben ein Merkmal
gemeinsam: Man gibt eine Drittelfigur vor und halbiert dann die Restfigur.
Das führt zu einem Paar kongruenter Teilfiguren. In einigen Fällen
sind alle Teilfiguren kongruent.
Dreiteilung von
Körpern
top
Man kann die Figuren oben zu Prismen bzw. Zylindern ergänzen,
indem man die Figuren zu ihren Grundflächen macht.
Prismen
...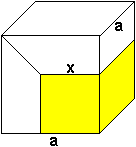 ... ... |
Als Beispiel dient die Aufteilung in ein Quadrat und
zwei rechtwinklige Trapeze, die zu einem Würfel ergänzt werden. |
Würfel
...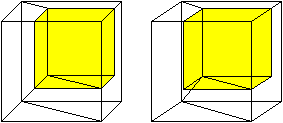 ... ... |
Man kann das Quadrat auch zu einem Würfel werden
lassen. Dann ergibt sich die nebenstehende Aufteilung in 3D-Ansicht.
Es gilt x³=(1/3)a³ oder x=(1/3)*3^(2/3)a oder
ungefähr x=0,69a |
Zylinder
oder Kugel
...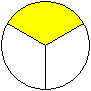 ... ... |
Man kann die nebenstehende Figur in zweierlei Weise dreidimensional
deuten.
Sie kann einen Zylinder oder eine Kugel darstellen, die
in drei gleiche Teilkörper aufgeteilt sind. |
Pyramiden
im Würfel
...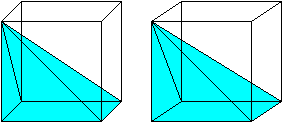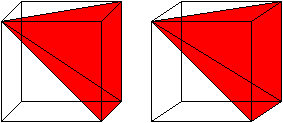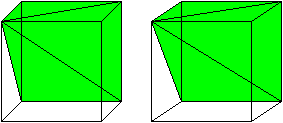 ... ... |
Drei Pyramiden gleicher Grundfläche, gleicher Höhe
und damit gleichen Volumens passen in einen Würfel.
So kann man den Faktor 1/3 in der Volumenformel der Pyramide
einsehen.
Das ist eine 3D-Ansicht. |
...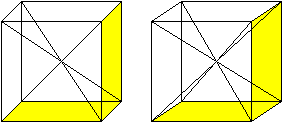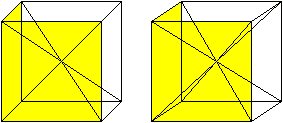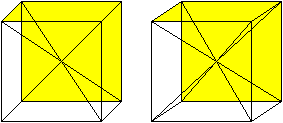 ... ... |
Zeichnet man die Raumdiagonalen eines Würfels, so
teilen diese ihn in sechs quadratische Pyramiden. Setzt man zwei Pyramiden
mit einer gemeinsamen Seitenfläche zu einem neuen Körper zusammen,
so erhält man eine Dreiteilung in kongruente Körper.
Rechts werden der Klarheit halber nur die Grundflächen
der Pyramiden gelb gekennzeichnet. |

Eine Fundgrube
Dreiteilung
des Winkels im Internet top
Deutsch
Jutta Gut
Die
Dreiteilung des Winkels
Matroids Matheplanet
syn: Winkeldreiteilung
und der Satz von Haga, Florian Modler: Der
Schmetterling und der Satz von Morley
Wikipedia
Dreiteilung
des Winkels, Klassische
Probleme der antiken Mathematik,
Englisch
Alexander Bogomolny (Cut The Knot)
Angle
Trisection by Archimedes of Syracuse, Angle
Bisector
Eric W. Weisstein (MathWorld)
Angle
Trisection
Wikipedia
Angle
trisection,
Exact
trigonometric constants, Morley's
trisector theorem
Referenzen top
(1) W. Breidenbach: Die Dreiteilung des Winkels, Leipzig
1933
(2) Jan Gullberg: Mathematics- From the Birth of Numbers,
New York, London 1997 (ISBN0-393-04002-X)
Seite 423 ff.
(3) Martin Gardner: Mathematischer Karneval , Ullstein
Berlin-FrankfurtMain-Wien, 1975 (ISBN 3 550 07675 4)
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2009 Jürgen Köller
top |
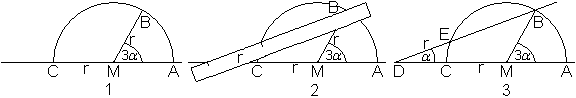



 ...
... ...
...

 ...
... ...
...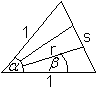 ...
...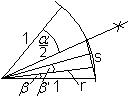 ...
... ...
...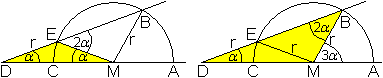 ...
... ...
...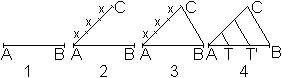








 ...
... ...
... ...
... ...
... ...
...