|
What is a Paper Cup?
... ... ... |
A paper cup is a cup which you can fold from a sheet
of paper.
If the paper is not printed inside and sturdy, you can
even drink from it. |
If the paper cup is large enough, you can turn it and use
it as a hat.
Folding of a Paper
Cup top
1
... ... ...
|
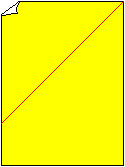
Take a sheet of paper of the size A4 (8 1/2" x 11"). Paper
used for ink jet printers will do.
Fold the upper half down on the red line.

 |
2
 ... ...
|
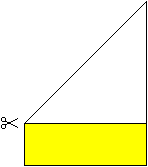
Cut off the lower strip.
 |
3
... ... ...
|
The result is a square.
 |
4
... ... ... |
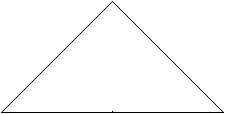
Fold the upper triangle downwards on the red line.  |
5
|
The result is a isosceles, right-angled triangle.
 |
6
|
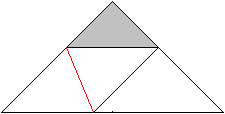
Fold the left corner upwards on the red line. Mind, that
you get a new isosceles, right-angled triangle (grey) and that its basic
side is parallel to the basic side of the whole triangle.
 |
7
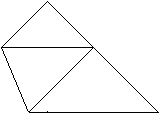
|
It must look like this.
 |
8
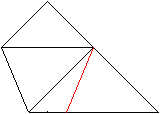 |
Fold the right corner upwards on the red line.
 |
9
... ... ...
|
It must look like this.
 |
10
|
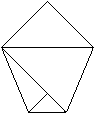
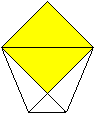
Fold the upper triangle downwards on the red line.
 |
11
|
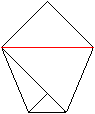
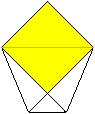
It must look like this. There is a second triangle.
 |
12
|
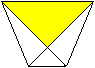
Fold this triangle backwards.
 |
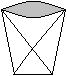
13
 ..... ..... ....... .......
|
Open it. The paper cup is finished. It has no stand.
 |
Variation top
...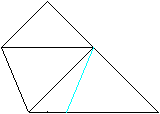 ... ... |
After step 1 to 7 fold the left triangle backwards at
the blue line.
Both triangles, in front and on the rear side, form pockets.
You can put in the upper triangles. You can cut them, so that they fit.
Then the paper cup looks better. |
Some Mathematics
top
If you unfold the paper, you can
recognize the shapes of the cup in the shape of a trapezoid.
...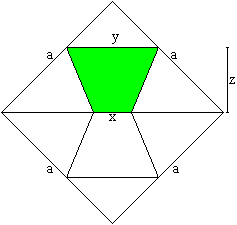 ... ... |
How can you calculate the measurements of the cup, when
the side of the square is given as a?
A trapezoid is given by the parallel sides x, y and the
height z for instance. |
If you like to calculate yourself, stop reading further.
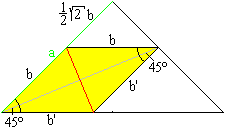 |
If you fold on the red line, you lay the left yellow
triangle on the right. Thus the yellow quadrilateral has the sides b and
b' twice. Both diagonals are perpendicular to each other. Therefore the
quadrilateral is a rhombus and all sides have the same length. The upper
triangle is isosceles and right-angled. Its two sides have the length sqr(2)/2*b.
If the side of the starting square is a (green), there
is a=b + sqrt(2)/2*b. Then b is [2-sqrt(2)]*a.
 |
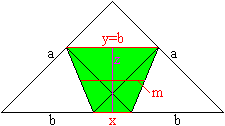 |
The trapezoid, which develops, is given by x, y and z.
There is:
x=sqrt(a)-2b = [3*sqrt(2)-4]*a
y=b=[2-sqr(2)]*a
z=[sqr(2)/2]*a - b/2 = [sqr(2)-1]*a
 |
The median is m=(x+y)/2=[sqrt(2)-1]*a =z. Thus the median
and the height of the trapezoid have the same lengths.
By the way the upper corners of the trapezoid devide
the side a in the ratio 1:sqrt(2). This is the ratio of the format
A.
Paper Cup on
the Internet top
German:
Andreas Bauer
Becher
- traditionell
Besser Basteln
Origami
Becher
Labbé (zzzebra)
Trinkbecher
aus Papier
Mathekiste
Symmetrie
und Papierfalten
origami.ch
Trinkbecher
English:
Kids Web Japan
Let's
Make Origami!
ViewDo LLC
Paper
cup (Video)
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
2003 Jürgen Köller
top |
 ...
... ...
... ...
... ...
... ...
...



 ...
...


 .....
..... .......
....... ...
... ...
...
