|
Was ist die archimedische Spirale?
...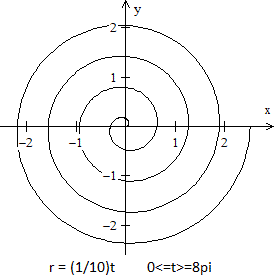 ... ... |
Die archimedische Spirale ist der Graph der Relation
mit der Polargleichung r(t) = kt.
Dabei ist die Variable k eine positive reelle Zahl.
Sie heißt auch Spirale des Bernoulli und
im Englischen Equiangular Spiral. |
Drei
Gleichungen top
Polargleichung
Die Spirale kann man durch eine Überlagerung zweier
Bewegungen eines Punktes erzeugen, nämlich durch eine gleichförmige
Bewegung längs eines Strahls von einem Anfangspunkt aus und durch
eine gleichförmige Kreisbewegung des Strahls um den Anfangspunkt herum.
... ... ... |
Die gleichförmige Bewegung links bewegt einen
Punkt nach rechts. - Das Bild enthält neun Momentaufnahmen. |
... ... ... |
Die gleichzeitig stattfindende gleichförmige Kreisbewegung
bringt die Punkte auf eine Spiralbahn.- Nach jeder Achteldrehung wird ein
Punkt gesetzt. |
...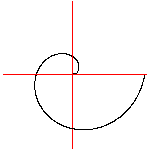 ... ... |
Die Spirale entsteht als Kurve, wenn der Ort zu jedem
Zeitpunkt festgehalten wird. |
...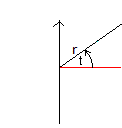 |
Bei der Spirale sind also Radius r(t) und Winkel t proportional.
So bietet sich die folgende Polargleichung an:
r(t) = kt (k ist im einfachen Fall eine positive
reelle Zahl). |
Parametergleichungen
...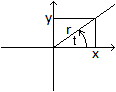 |
Die Parametergleichungen der archimedischen Spirale sind
x(t)
= kt cos(t) und y(t) = kt sin(t).
Herleitung
r = sqrt[x²(t)+y²(t)] = sqrt[k²t²cos²(t)+k²t²sin²(t)]
= sqrt[k²t²] = kt, wzbw.. |
Koordinatengleichung
Die Koordinatengleichung lautet
sqrt(x²+y²) = k*arc tan(y/x) oder tan[(1/k)sqrt(x²+y²)]=y/x.
Herleitung
Es gilt tan(t)=y/x oder t = arc
tan(y/x) und r = sqrt(x²+y²).
Das führt mit der Polargleichung
r=kt zur Koordinatengleichung sqrt(x²+y²) = k*arc tan(y/x) oder
tan[(1/k)sqrt(x²+y²)]=y/x.
Graph
... ...
...
|
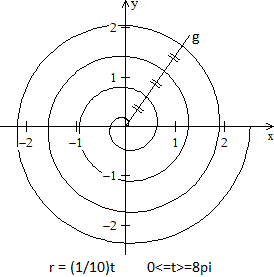
Die archimedische Spirale beginnt im Nullpunkt und beschreibt
um ihn eine immer weiter werdende Kurve.
Der Abstand der Spiral-Äste bleibt gleich. Genauer:
Die Entfernungen benachbarter Kurvenpunkte auf einer Nullpunktsgeraden
g sind gleich. |
Doppelspiraletop
...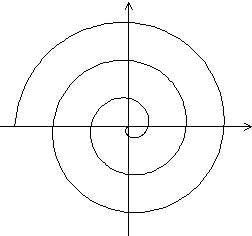 |
Eine Spirale erhält man auch mit der Polargleichung
r= - kt. |
...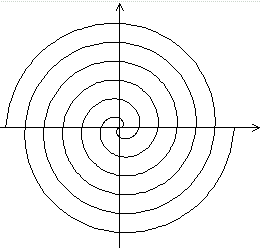 |
Die beiden Graphen zu r = kt und r= - kt bilden eine
Kurve, die auch als Doppelspirale bezeichnet wird. |
Kurvenstück
einer Spirale top
Die Länge eines Kurvenstücks einer Spirale
mit r=kt bis zum Winkel t beträgt L = (1/2)k[arsinh(t)+t*sqrt(1+t²)].
Herleitung
Ist eine Kurve in der Parameterform gegeben, so ist die
Länge eines Kurvenstücks
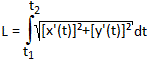
Für die Spirale heißt
das x(t) = kt*cos(t) und y(t) = kt*sin(t) und x'(t) = k*cos(t)-kt*sin(t)
und y'(t) = k*sin(t)+kt*cos(t) .
Weiter ist [x'(t)]² = k²cos²(t)-2k²t*sin(t)cos(t)+k²t²*sin²(t)
und [y'(t)]² = k²sin²(t)+2k²t*sin(t)cos(t)+k²t²*cos²(t)
und [x'(t)]²+ [y'(t)]² = k²+k²t²
= k²(t²+1). Die Wurzel ist k*sqrt(t²+1).
Also gilt es, das Integral aus sqrt(t²+1)dt zu lösen.
Da hilft eine Sammlung von Integralen mit ihren Stammfunktionen.
 Die gesuchte Länge ist dann
Die gesuchte Länge ist dann
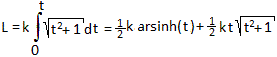
Zahlenbeispiel
k=1, t=pi
...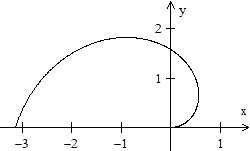 |
L = (1/2)k[arsinh(t)+t*sqrt(t²+1)] = (1/2)[arsinh(pi)+pi*sqrt(pi²+1)]
= (1/2)[1,862+10,357] = 6,109 LE |
Flächenstück
unter einer Spirale top
Der Flächeninhalt zwischen der Spirale mit r=kt
und einer Nullpunktsgeraden bis zum Winkel t beträgt A = (1/6)k²t³.
Herleitung
...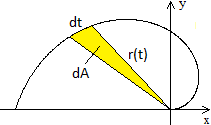 ... ... |
Man betrachtet einen Ausschnitt zwischen zwei Radien
und einem Kurvenstück dt. Er kann als Kreisausschnitt angenommen werden,
wenn dt hinreichend klein ist.
Für den Flächeninhalt dA gilt dann dA:(pi*r²)
= dt:(2pi) oder dA = (1/2)r²dt = (1/2)(kt)²dt.
Für den Flächinhalt A gilt "Integral von 0
bis t von (1/2)(kt)²dt".
Das heißt, A = (1/2)k²(1/3)t³ = (1/6)k²t³,
wzbw.. |
Zahlenbeispiel
k=1, t=pi
...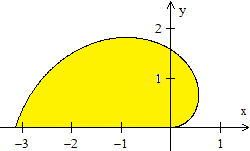 |
A = (1/6)k²t³ = (1/6)pi³ oder ungefähr
5,168 FE |
Bänder aufwickeln
top
... ... ... |
...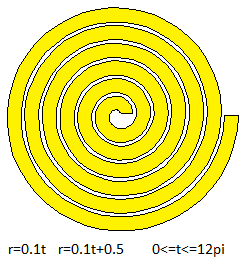 ... ... |
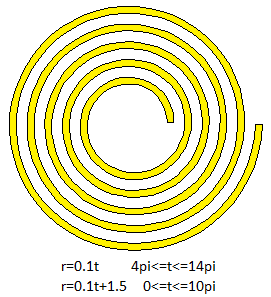
Man kann wie links ein Band in Form einer archimedischen
Spirale aufwickeln. Dabei berühren sich die Ränder.
Beispiele: Lakritz-Schnecke, Rosinenschnecke, Papierrolle,
Klebeband, Schlange, ... |
Zum
Klebeband
...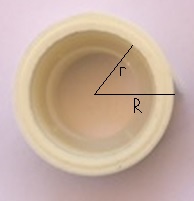 ... ... |
Dünne Bänder sind sperrig, besser man rollt
sie auf.
Die Rolle des Klebebandes links z.B. bildet eine archimedische
Spirale. Weil die Dicke des Bandes d aber wesentlich kleiner als die Dicke
der Bandschicht R-r ist, kann man an Stelle der Windungen konzentrische
Kreise annehmen. Wird das Klebeband abgerollt, so bildet es in der Seitenansicht
ein Rechteck mit den Maßen d und L, wobei L die Länge des Bandes
ist. Dann ist der Flächeninhalt der Bandschicht d*L. Andererseits
ist der Flächeninhalt der Bandschicht auch gleich pi*R²-pi*r².
Das führt zur Formel dL = pi*R²-pi*r² oder L = (1/d)pi(R²-r²).
Die Anzahl n der Windungen ist n=(R-r)/d. |
Zahlenbeispiel,
Gegeben: d=0,06mm, R=2,25cm=22,5mm, r=1,75cm=17,5mm
L = (1/0,06)pi(22,5²-17,5²) mm = 1047 mm. Das
ist etwa 1m.
n = (22,5-17,5)/0,06 = 83
Quelle: https://rechneronline.de/rolle
Archimedische
Spirale im Internet top
Deutsch
Jürgen Kummer (rechneronline.de)
Rolle berechnen:
Länge, Wicklungen, Durchmesser des Bandes
Wikipedia
Archimedische
Spirale
Englisch
Eric W. Weisstein (MathWorld)
Archimedes'
Spiral
Robert FERRÉOL (Mathcurve)
ARCHIMEDEAN
SPIRAL
MacTutor History of Mathematics archive [University
of St Andrews, Scotland]
Spiral
of Archimedes
Wikipedia
Archimedean
spiral
Feedback: Emailadresse auf meiner Hauptseite
URL meiner Homepage:
https://www.mathematische-basteleien.de/
© August 2018 Jürgen
Köller
top |
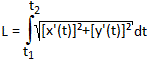
 ...
... ...
... ...
...

 ...
...

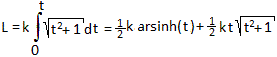
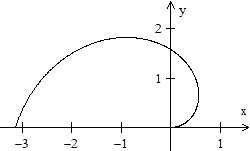
 ...
...
 ...
... ...
... ...
...