|
What is a Pyramid?
... ... ... |
Give a plane polygon and a point, which isn't inside
the plane of the point.
If you connect this point with the corners of the polygon,
you get a (general) pyramid. |
... ... ... |
... ... ... |
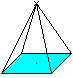
If the polygon is a square and the point lies over the
centre of the square, the straight square pyramid, shortly called pyramid,
develops. The following site relates to this regular pyramid. |
... ... ... |
Pieces of the Pyramid
top
Lengths
...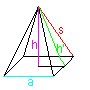 ... ... |
The pyramid is determined by the side a of the base and
the height h.
The triangular side s and the triangular height h' are
further lines. |
Angles
...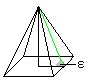 ... ... |
The angle between a triangle and the base (angle of inclination)
is typical for the form of the pyramid. |
Surface
...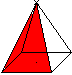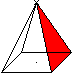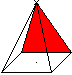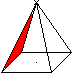 ...... ...... |
The four lateral faces form M (M=2ah').
The lateral surface O consists of the base and the lateral
faces. (O=a²+2ah').
(German: Mantel M=coat, Oberfläche O=lateral faces) |
Volume
...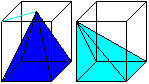 ... ... |
If you put a rectangular solid with the volume a²h
around the pyramid and move the vertex to the corners of the solid, you
get a crooked pyramid with the same volume. There are two additional pyramids
of the same volume. They all fill the solid.
The volume of one pyramid is V=(1/3)*a²h. |
...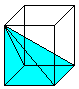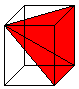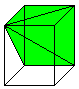 ... ... |
Pyramid and Cube
top
If you succeed in making the 3D-view, you can three-dimensionally
look at the following three cube pairs.
...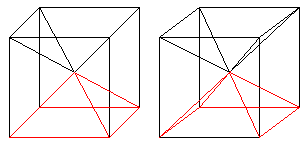 ... ... |
If you draw the four space diagonals of a cube, the cube
is divided in six equal pyramids. The height of a pyramid is a/2. There
is V=a³/6=a²*(2*h)/6=(1/3)*a²*h. This again is the well
known formula for the volume of a pyramid. |
The angle of inclination is 45°.
... ... ... |
If you connect the centre of one square and the
corners of the opposite square, then a pyramid with the feature h=a develops.
The angle of inclination is arc tan(2)=63.4°. |
Equilateral Pyramid top
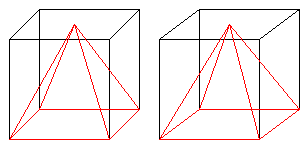
... ... ... |
If all edges of a pyramid are the same (a=s) and if you
reflect it at the base square, a double pyramid develops, which is only
formed by equilateral triangles. This solid of eight triangles is called
an octahedron.
The angle of inclination of the pyramid with the equilateral
triangles is
arc cos[sqrt(3)/3]= 54,7°.
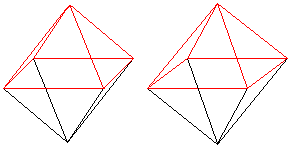
|
The octahedron (the same as the tetrahedron, the cube, the
dodecanhedron, and the isocahedron) belongs to the regular polyhedra or
Platonic solids.
You can also produce an octahedron by connecting
the centres of the squares of a cube by lines. Cube and octahedron are
dual.
Pyramidal Numbers
top
...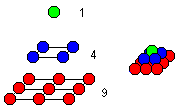 ... ... |
You can build a pyramid with layers of spheres. The number
of the spheres in one layer is a square number: 1,4,9,16,... , generally
n². If you add the spheres layer by layer, you get the pyramidal numbers
1,5,14,30,... , generally 1+4+9+16+...+n²=n(n+1)(2n+1)/6. |
In former times people kept cannon balls in such a way. They
could easily count them by counting the number of the layers.
...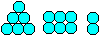 ... ... |
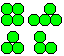
If you glue 14 marbles to two groups with six and to
one pair, you get a puzzle: You must form a pyramid with three pieces. |
... ... ... |
This puzzle is more complicated. ........................... |
It looks nice, if you form a pyramid with single marbles.
Then the marbles in the lowest layer must lie in half rounds or in a framework.
The Great Pyramid of Gise top
If you speak about pyramids, you
usually mean the Great Pyramid, Pharao Cheop's tomb, from the 4th dynasty
(2500 BC) situated 15km south of the centre of Cairo in sight of the Nile
in Epypt.
Cheop's pyramid is a building with
a string of superlatives: It is one of the Seven Wonders of the World,
which is mainly preserved. It was the largest building up to the modern
era. It is one of the most famous buildings of the world.
...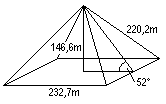 ... ... |
The measurements of Cheop's pyramid differ in the literature.
I use the data of a new travel guide (5) hoping the last researches are
considered. Today the pyramid is 137.0m high and 230.5m long. Originally
it was a little larger (on the left). It covers an area of about 5 ha.
About 2,5 millions blocks with a volume of nearly 1m³ form the pyramid.
The covering of polished lime plates is not preserved. |
If you give the original data a=232.7m and h=146.6m, the
edges are s=220.4m, the base 5.4150 ha, the lateral faces 8.7120 ha, the
lateral surface 14.13 ha, the volume 2646000 m³ and the angle of inclination
51.6°.
The volume is illustrated. If you let a stone block be
a cube with the edge 1m, you can form a line 2500km long. This is nearly
the
distance London - Athens.
Number
Mysticism of the Great Pyramid top
Statements, Comments
1
...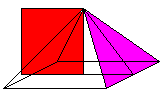 ... ... |
Area of the square above the height:
h² = 21780m².
Area of a triangle side: (1/2)*a*h' = 21490m².
Supposed: The areas are the same.
(Herodot). |
The equations h²=(1/2)*a*h' and h²+a²/4=h'²
(Pythagorean Theorem) lead to the ratio a:h= sqr(sqr(20)-2)=1,5723... .
This is about 3.1446../2 or Pi/2.
Both equations result in the second ratio h':(a/2)=1/2*[1+sqr(5)].
This is the golden ratio phi = =1.6180... .
2
...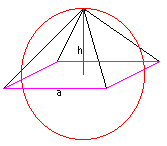 ... ... |
Perimeter of the square base: 4a=930.8m
Perimeter of the circle with the radius h: 2*PI*h=921.1m
Supposed: The perimeters are the same. |
... ...circle ...circle |
The ancient Egypts knew the
ratio (circle perimeter : circle diameter) as 256/81 (Rhind Papyrus
1850 BC). This leads to Pi=3.16... (book 4).
The circle as a symbol for the
sun was very important in the ancient Egyptian mythology and decorates
the head of the Goddess Hathor (on the left) for instance.
The ratio was explained on TV
by Hoimar von Ditfurth (5) this way: A circle is unrolled along a square
side of Cheop's pyramid and the same circle is piled up along the height.
So the ratio [perimeter : diameter]=PI appears at the pyramid. |
3
...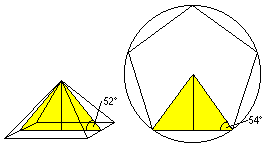 ... ... |
If you lay a vertical section through the centre of a
pyramid parallel to one square side, you get a (yellow) triangle. This
triangle is almost the main triangle of a pentagon.
It is special that two diagonals of a pentagon divide
each other in the golden ratio. |
You can often see a sky with
five-cornered stars on a blue background in tombs.
4
...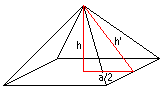 ... ... |
The red triangle has the ratio chain
h' : h : a/2 = 5 : 3.90 : 3.11. This is nearly 5 : 4
: 3 with
5² = 4² + 3². The numbers 3,4,5
are Pythagorean numbers.
Supposed: The triangle is a Pythagorean triangle. |
After the annual flood of the Nile
the fields were measured by 3-4-5-strings with knots.
5
...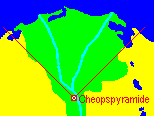 ... ... |
The base of the pyramid is lined up in the four points
of the compass.
If you extend the diagonals of the base square, these
lines include the Nile delta. |
The position of the Great
Pyramid is remarkable, especially as you can look far into the Nile delta,
if the smog of Cairo permits.
6
...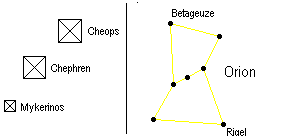 ... ... |
The Great Pyramid is not isolated. It nearly forms a
straight line with Chefren's and Mykerinos' pyramids. The constellation
Orion's three belt stars form (formed 4500 years ago) a similar line. Besides
there are two more pyramids, which correspond to two corner stars of Orion.
(Source: Robert Bauval, quoted in a report of the German TV station ZDF. |
Summary:
It is certain, that the ancient Egyptians chose the measurements
of the pyramid in order to make it safe and nice.
Who knows? Perhaps mysterious laws are hidden in the
pyramids.
On the other hand: Numbers are patient... as we say
in Germany.
The Power of Pyramids
top
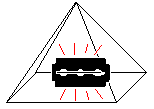
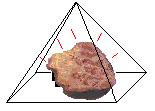
In the American magazine "Scientific
American" from June, 1974 a Dr.Matrix reported about a power, which came
from pyramids. Mysterious events happened in small models of pyramids:
Razor blades became sharp again, meat rotted slower, and a person sitting
inside a pyramid got supernatural abilities. These statements were proved
by reports from all over the world and seemed to be true.
Stop ;-) !
This was a scientific joke. The yearning for esotericism,
which arose at that time, should be satirized. - The famous journalist
of "Scientific American" Martin Gardner wrote this article.
I am interested, whether people sat inside small pyramids
before June 1974 ;-).
Calculations
top
A pyramid is usually given by the
square side a and the height h. Other pieces, triangle side s, lateral
faces M, or volume V can be calculated by them. There are the following
formulas.
s²=h² + a²/2
M²=a^4
+ 4a²h²
V=1/3*a²h
You can generalize: If two of the five
pieces a,h,s,M, and V are given, the remaining pieces can be calculated.
There are ten cases:
1) Given: a,h. Search: V,s,M.
Solution: V=1/3a²h, s=1/2*sqr(2a²+4h²),
M=a*sqr(a²+4h²).
2) Given:
a,s. Search: h,V,M.
Solution: h=1/2*sqr(4s²-2a²),
V=1/6*a²*sqr(4s²-2a²), M=a*sqr(4s²-a²).
3) Given:
h,s. Search: a,V,M.
Solution: a=sqr(2s²-2h²),
V=2/3*h*(s²-h²), M=2*sqr(s^4-h^4).
4) Given:
a,V. Search: h,s,M.
Solution: h=3V/a², s=1/2*1/a²*sqr(2a^6+36V²),
M=1/a*sqr(a^6+36V²).
5) Given: h,V. Search: a,s,M.
Solution: a=1/h*sqr(3hV), s=1/2*1/h*sqr(4h^4+6hV),
M=1/h*sqr(9V²+12h³V).
6) Given: s,V.
Search: h,a,M
Solution: h³-s²h+3/2*V=0
und a^6-2s²a^4+18V²=0 must be solved:-(, then M=a*sqr(a²+4h²).
7) Given: a,M.
Search: s,h,V.
Solution: s=1/2*1/a*sqr(M²+a^4),
h=1/2*1/a*sqr(M²-a^4), V=1/6*a*sqr(M²-a^4).
8) Given: h,M.
Search: s,a,V.
Solution: s=1/2*sqr[sqr(4M²-16h^4)],
a=sqr[sqr(M²-4h^4)-2h²)],
V=1/3*h*[sqr(M²-4h^4)-2h²].
9) Given: s,M.
Search: h,a,V.
Solution: h=1/2*sqr[sqr(16s^4-4M²)],
a=sqr[2s²-sqr(4s^4-M²)],
dann V=1/3*a²h.
10) Given: M,V.
Search: a,h,s.
Solution: a^6-M²a²+36V²=0
und 12Vh³-M²h²+9V²=0 must be solved:-(, then s=1/2*sqr(2a²+4h²).
(Thanks to 10b in 1992/93)
An Example:
(Give M,V):
Which shape has a pyramid, which
has the same volume and the same lateral faces as the Great Pyramid of
Gise?
Solution: You derive the equation
h³ - (M²/12/V)*h² + (3/4)*V = 0.
You get with V=2646000 and
M=87120 the solutions h1=146.6, h2=171.4, and h3= -79,0 (found with
DERIVE).
...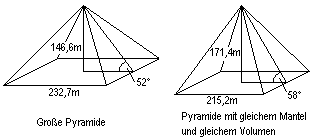 ... ... |
The height h2=171.4m is the second solution.
The square side a2=215.2m belongs to the height h2. |
This isn't a new contribution to the pyramid research.
This only is fun.
Largest Pyramid
top
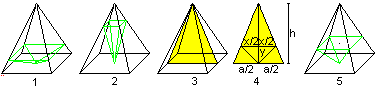 You can headfirst lay a second pyramid (green) inside a pyramid.
Its vertex is in the centre of the base and its square is parallel to the
base of the large pyramid. If the green pyramid is very low (1) or pointed
(2), its volume is small. There is a pyramid between, which is maximum.
It is the pyramid on the right (5).
You can headfirst lay a second pyramid (green) inside a pyramid.
Its vertex is in the centre of the base and its square is parallel to the
base of the large pyramid. If the green pyramid is very low (1) or pointed
(2), its volume is small. There is a pyramid between, which is maximum.
It is the pyramid on the right (5).
You find this pyramid in the following way.
You lay a yellow triangle (3) inside the given pyramid,
and introduce the square side x and the height y. The volume is V=1/3*x²y.
With the help of the equation h:(h-y) = a:x you get V(x)=1/3*hx²-1/3*h/a*x³.
You get x=2/3*a and further y=1/3*h by V'(x)=0.
Pyramids on
the Internet top
German
Christian Tietze/Rico Hecht
Architekturmodelle
von Pyramiden
(Zur Ausstellung „Pyramide – Haus für die Ewigkeit“
ab 6. September 2001 im Römisch-Germanischen Museum in Köln)
Frank Dörnenburg
Rätselhafte
Pyramiden
Ingrid Huber (Hubsi's Lehrer Homepage)
Grundwissen
über Pyramiden
Wikipedia
Pyramide,
Pyramide
(Bauwerk), Pyramide
(Geometrie)
English
Andrew Bayuk (Guardian's CyberJourney To Egypt)
The
Great Pyramid
Eric W. Weisstein (MathWorld)
Pyramid,
Square
Pyramid,
Square
Pyramidal Number
FERCO
The
Pyramids of Guimar
Unter Leitung des Ethnologen Thor Heyerdahl entstand
in Teneriffa ein Pyramiden-Museum. Es wird die (umstrittene) Theorie belegt,
dass es einen Zusammenhang zwischen den Pyramiden in Ägypten
und in Mittelamerika gibt. Trotzdem: Ein interessantes und geschmackvoll
eingerichtetes Museum.
Kevin Matthews and Artifice, Inc. (greatbuildings.com)
Sources
on Great Pyramid of Khufu, Pyramide
du Louvre
Lee Krystek
Khufu's
Great Pyramid
Tim Hunkler
The Great
Pyramid as Proof of God
Wikipedia
Pyramid,
Pyramid
(geometry)
References
top
(1) Lancelot Hogben: Die Entdeckung der Mathematik, Stuttgart
1963
(2) Martin Gardner: Die magischen Zahlen des Dr. Matrix,
Frankfurt am Main 1987
(3) Armando Curcio (Hrg.): Meilensteine der Archäologie,
Herrsching 1987
(4) David Blatner: Pi, Magie einer Zahl, Reinbek bei
Hamburg 1997
(5) FTI Touristik Publications: Reisebegleiter Ägypten,
2000?
(6) "Gibt es ein Geheimnis der Pyramiden?" Two TV reports
from the series "Querschnitt" by Hoimar von Ditfurth, ZDF (29.03.1976 und
05.04.1976, repeated in 1991)
In these two TV reports Hoimar von Ditfurth reacted
to Erich von Däniken's bestseller "Erinnerungen an die Zukunft" with
the speculation: "The pyramids were built with the help of extraterrestrial
beings".
The report said: "The ancient Egypts already had the
abilities
to build the pyramids."
Comments top
I made this website after a sight-seeing tour through
Epypt including the pyramids of Gise in April 2001.
Gail from Oregon Coast, thank you for supporting
me in my translation.
Feedback: Email address on my main page
This
page is also available in German
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
2001 Jürgen Köller
top |
 ...
... ...
... ...
... ...
...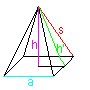 ...
...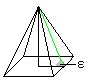 ...
... ......
...... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...circle
...circle  ...
... ...
... ...
... ...
...
 ...
...