Was ist der asymmetrische Propeller?
Der asymmetrische Propeller ist eine Figur der Unterhaltungsmathematik. 
Er besteht aus drei (gelben) gleichseitigen Dreiecken, die sich in einem Eckpunkt treffen.

......

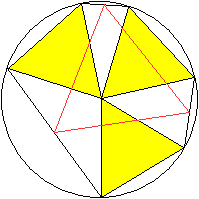Das Besondere ist, dass ein weiteres (rotes) gleichseitiges Dreieck auftritt. Verbindet man nämlich wie in der Zeichnung die freien Eckpunkte der Dreiecke miteinander und halbiert die Verbindungsstrecken, so bilden ihre Mittelpunkte ein gleichseitiges Dreieck. Das ist der Satz vom asymmetrischen Propeller.

......

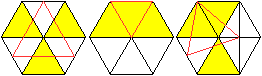Der Satz gilt für alle Anordnungen der Dreiecke. Der Propeller kann selbstverständlich symmetrisch sein und die Dreiecke können Seiten gemeinsam haben (dazu die Bilder).  Sie können sich auch überlappen.

Beweis des Satzes    top
1

......

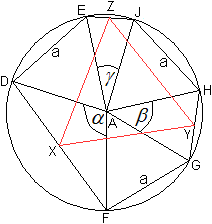Führe die folgenden Bezeichnungen ein.  Die Ausgangsdreiecke seien ADE, AJH und AGF, die Seitenlänge sei a. Die Halbierungspunkte der Strecken FD, HG und EJ seien X, Y und Z. Die Winkel zwischen den Dreiecken seien alpha, beta und gamma. Ihre Summe ist 180°. Zu zeigen ist, dass das Dreieck XYZ gleichseitig ist oder dass alle Innenwinkel 60° betragen.

......

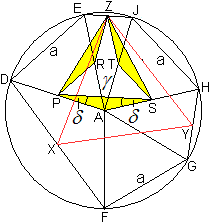Die gelben Dreiecke sind kongruent, denn zwei Seiten mit den Endpunkten A, R oder T und die stumpfen Winkel zwischen den Seiten sind gleich. Die Seiten sind nämlich als Mittelparallelen im Dreieck gleich a/2,  die Winkel sind gleich 120°+gamma . Daraus folgt, dass das Dreieck PSZ gleichseitig ist. Die Winkel APS und ASP, die im nächsten Beweisschritt benötigt werden, betragen  delta=(1/2)[180°-(120°+ gamma)] = (1/2)(60°- gamma).

......

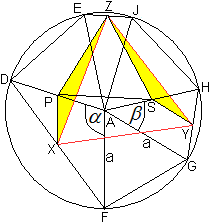Die gelben Dreiecke sind kongruent, denn sie stimmen in den beiden kürzeren Seiten überein. Die Seite SY ist nämlich als Mittelparallele im Dreieck AGH gleich a/2, dsgl. PX im Dreieck FAD, und es gilt PZ =ZS, weil das Dreieck PSZ nach Schritt 2 gleichseitig ist. Eine kleine Rechnung zeigt weiter, dass die Winkel bei P und S gleich sind.  Winkel XPZ = Winkel YSZ 60°+ delta +(180°- alpha) = 360°-[60°+delta+(180°- beta)] 240°+ delta -alpha = 120° - delta + beta 120°+2*delta - alpha - beta = 0 alpha + beta + gamma =180° Die Rechnung wird logisch richtig, wenn von unten nach oben gelesen wird.

Verallgemeinerungen  top

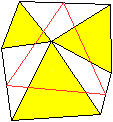...	Die drei gleichseitigen Dreiecke müssen nicht unbedingt gleich groß sein.

......

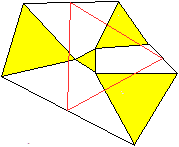Die drei gleichseitigen Dreiecke gehen nicht von einem Punkt aus, sondern von den Eckpunkten eines weiteren gleichseitigen Dreiecks.

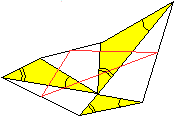...	Die drei Dreiecke müssen nicht gleichseitig sein, sie können ähnlich sein. .............. Dabei rotiert jedes der drei Dreiecke relativ zum Nachbarn.  Das "Mittendreieck" ist den anderen Dreiecken ähnlich.

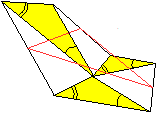...	So können sich die Dreiecke z.B. auch anders berühren......................................................

......

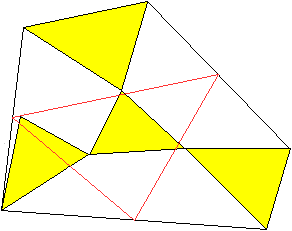Eine Verallgemeinerung erfolgt also in zwei Richtungen: >Die beteiligten Dreiecke müssen nicht gleichseitig sein, sondern nur ähnlich.  >Die drei Dreiecke gehen nicht von einem Punkt aus, sondern von den Eckpunkten eines dazu ähnlichen Dreiecks. Dabei berühren sich korrespondierende Punkte. Jedes der drei Dreiecke rotiert relativ zum Nachbarn.  Ergebnis: Das (rote) resultierende Dreieck ist zu den anderen Dreiecken ähnlich.

Napoleon-Dreieck   top
Es liegt nahe, in diesem Zusammenhang auf das Napoleon-Dreieck hinzuweisen. Es besteht auch aus drei zusammenhängenden, gleichseitigen Dreiecken.

......

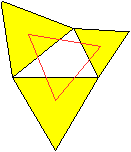Gegeben ist ein beliebiges Dreieck.  Errichtet man über seine Seiten gleichseitige Dreiecke, so bilden ihre Mittelpunkte wiederum ein gleichseitiges Dreieck.

......

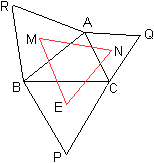Führe Bezeichnungen ein:  Das Ausgangsdreieck sei ABC. Die gleichseitigen Dreiecke seien BPC, BRA und CAQ. Zeige, dass das Dreieck EMN gleichseitig ist. Hier wird  gezeigt, dass alle Innenwinkel 60° betragen.

......

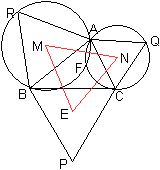Zeichne die Umkreise der Dreiecke BRA und CAQ. Sie schneiden sich in A und im neuen Schnittpunkt F.........................................................................

......

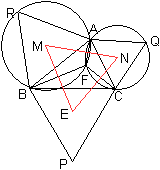Verbinde Punkt F mit den Punkten A, B und C.  Es entstehen die Sehnenvierecke BRAF und CFAQ.  Die Winkel bei R und Q betragen 60°, dann sind die Winkel BFA und CFA 120°. Folglich ist im Viereck PBFC der Winkel BFC auch 120°. Der Gegenwinkel CPB ist 60°. Dann ergänzen sich die Gegenwinkel zu 180°.  Das Viereck PBFC ist somit auch ein Sehnenviereck und hat einen Umkreis um E. Er ist in der nächsten Zeichnung eingetragen.

......

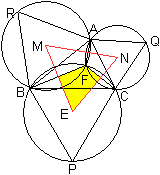Da FA, FB und FC Sehnen in Zweikreisfiguren sind und senkrecht auf den Verbindungsstrecken der Mittelpunkte, die gleichzeitig Dreiecksseiten sind, stehen, müssen die Winkel im roten Dreieck 360°-120°-90°-90°=60° groß sein.  Das war zu zeigen.

......

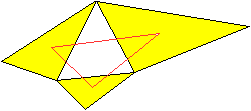Eine Verallgemeinerung besteht zum Beispiel darin, dass man über den Seiten eines beliebigen Dreiecks nicht gleichseitige, sondern ähnliche Dreiecke errichtet.  Dabei rotiert jedes der drei Dreiecke relativ zum Nachbarn.  Ergebnis: Das (rote) resultierende Dreieck aus den Schwerpunkten der Dreiecke ist zu den drei Dreiecken ähnlich.

Asymmetrischer Propeller im Internet     top

Englisch

A. Bogomolny (cut-the-knot)
Asymmetric Propeller,  AsymmetricPropeller2  (Applets and Explanations),

Martin Gardner  (MAA Writing Awards )
The Asymmetric Propeller   (.pdf file)

Rouben Rostamian
The asymmetric propeller   (Applet)

The Wolfram Demonstrations Project
Asymmetric Propeller

Zvonko Cerin
On Propellers from Triangles

Napoleon-Dreieck im Internet  top

Deutsch

Wkipedia
Napoleon-Dreieck

Englisch

A. Bogomolny (cut-the-knot)
Napoleon's Theorem and Generalizations, 
darunter Napoleon Propeller, 
daraus das Zitat "Napoleon's theorem is equivalent to the Asymmetric Propeller's theorem! How small is the world!"

Weisstein, Eric W (MathWorld)
Outer Napoleon Triangle,  Inner Napoleon Triangle 

Antonio Gutierrez 
Napoleon's Theorem

Jim Loy
Napoleon's Theorem

MathPages
Napoleon's Theorem

Wikpedia
Napoleon's theorem

Referenzen     top
(1) Martin Gardner: The asymmetric Propeller, The College Mathematics Journal [ Vol. 30, (1999), pp. 2-12]
Im Internet jetzt zugänglich, URL oben