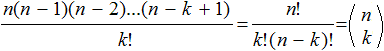Was bedeutet die Zahl 13 983 816?
13 983 816 ist die Anzahl der Möglichkeiten, aus 49 Zahlen eine Kombination von sechs Zahlen zu bilden.
Sie werden als Sechs Richtige in Deutschland beim Lottospiel in jeder Woche zweimal nach dem Zufallsprinzip ausgelost. 
Zum Beispiel waren 14,  25,  31,  32,  41 und  49 die Lottozahlen am Mittwoch, den 25.3.2009.
Die Reihenfolge war 31, 49, 25, 32, 41 und 14, aber auf sie kommt es nicht an. 

Füllt man vor einer Ziehung einen Lottoschein aus, gibt ihn bei einer Annahmestelle ab und und zahlt dabei 1 € pro Tipp, kann man mit der richtigen Vorhersage der Lottozahlen reich werden.

3 aus 6    top
Zum Einstieg wählt man am besten einen einfachen Fall. 
Statt 6 aus 49 geht es zuerst einmal um 3 aus 6. 
Gegeben sind also die Zahlen 1, 2, 3, 4, 5 und 6. Aus ihnen sollen 3 beliebige Zahlen (3-Tupel oder Tripel) ausgewählt werden. 
Sie sollen wie beim Lotto voneinander verschieden sein, und auf die Reihenfolge soll es auch nicht ankommen. 

Unter diesen Bedingungen gibt es 20 Tripel, hier systematisch bestimmt und der Größe nach geordnet:

Noch einmal 3 aus 6       top
Ich sehe keinen Weg, dieses Vorgehen auf 6 aus 49 zu übertragen. 
Deshalb wird die Anzahl 20 noch einmal wie in (1), Seite 26 ff. hergeleitet. 

Man bildet alle Tripel aus 6 Zahlen, nun aber unter Berücksichtigung der Reihenfolge. 

123 124 125 126 132 134 135 136 142 143 145 146 152 153 154 156 162 163 164 165

213 214 215 216 231 234 235 236 241 243 245 246 251 253 254 256 261 263 264 265

312 314 215 216 ........................... ........................... ........................... 361 ..............365

412 413 415 416 ........................... ........................... ........................... 461 ..............465

512 513 514 516 ........................... ........................... ........................... 561 ..............564

612 613 614 615 ........................... ........................... ........................... 651 ..............654

Man kommt auf (5*4)*6=120 Tripel.
Greift man 3 verschiedene Zahlen wie 123 heraus, so sind  zu diesem Tripel in der Tabelle noch die Kombinationen 132, 213, 231, 312 und 321 vorhanden. Die 120 Tripel können also in Klassen zu je 6 Tripeln eingeteilt werden. 
Folglich muss man die Anzahl 120 noch durch 6 dividieren, wenn es auf die Reihenfolge nicht mehr ankommt. 
So gelangt man wieder zur Anzahl 20 wie oben.

6 aus 49     top
Nach dem Muster "Noch einmal 3 aus 6" könnte man für 6 aus 49 auf die Anzahl 13 983 816 kommen. 
Aber es ist erstrebenswert und günstig, von 6 aus 49 gleich auf den Fall k aus n überzugehen. 
Man leitet eine allgemeine Formel her und spezialisiert sie dann auf k=6 und n=49.

k aus n    top
Gegeben sind also die Zahlen 1,2,3,...,n und eine Zahl k mit k<n.
Gesucht ist die Anzahl der Möglichkeiten, aus den n Zahlen alle k-Tupel unter Berücksichtigung der Reihenfolge zu bilden. Man nennt sie in der Kombinatorik Variationen k-ter Ordnung, im Mangoldt/Knopp noch Kombinationen k-ter Ordnung mit Beachtung der Reihenfolge.

Voraussetzung: Die Anzahl der Variationen k-ter Ordnung für n Zahlen ist n(n-1)(n-2)...(n-k+1).
Zu zeigen:  Die Anzahl der Variationen (k+1)-ter Ordnung für n Zahlen ist dann n(n-1)(n-2)...(n-k+1)(n-k).
Zum Beweis:
Man kennt die Anzahl der Variationen k-ter Ordnung. Geht man auf die Ordnung k+1 über, so gibt es n-k Zahlen, die nicht unter den Variationen k-ter Ordnung sind und eingeordnet werden müssen. Fügt man diese Zahlen den Variationen k-ter Ordnung systematisch hinzu, erhält man das (n-k)-fache der Variationen k-ter Ordnung. 
Das ist die Anzahl der Variationen (k+1)-ter Ordnung n(n-1)(n-2)...(n-k+1)(n-k), w.z.b.w..

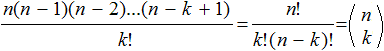
Der rechte Term wird gelesen als n über k und heißt  Binomialkoeffizient.

Noch einmal 6 aus 49      top
Setzt man k=6 und n=49, so gilt:
n!/[k!(n-k)!]=49!/(6!43!)=(49*48*47*46*45*44)/(2*3*4*5*6)=13983816.

Lotto im Internet top

Deutsch

Christoph Caspari
Lotto

Friedrich Cordes
Lotto 6 aus 49

Georg Einfalt
Georgs Lottozahlengenerator

Bernhard Berchtold (mathematik.ch)
Simulation der Ziehung beim Schweizer Zahlenlotto

Wikipedia
LOTTO, Glücksspiel, Hypergeometrische Verteilung,  Fakultät (Mathematik),  Binomialkoeffizient

Wikipedia
Lottery

Referenzen   top
(1) H. von Mangoldt / K. Knopp: Einführung in die höhere Mathematik, Leipzig 1958
(2) http://www.dielottozahlen.de/