|
Was ist eine Geradengleichung?
... ... ... |
Eine Gerade ist eine Linie, die entsteht, wenn man einen
Stift entlang eines Lineals führt. Sie ist ein Element der euklidischen
Geometrie.
Will man diese durch Axiome begründen, so ist das
sehr aufwändig, wie Hilberts Axiomensystem (URL unten bei Wikipedia)
zeigt. |
Man erfasst die Gerade einfacher
in der analytischen Geometrie.
Man betrachtet die Ebene als Punktmenge und führt
ein Koordinatensystem ein, um die Punkte zu lokalisieren.
...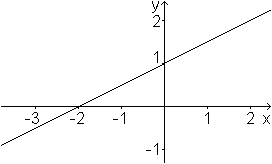 ... ... |
Eine Gerade entsteht im kartesischen
Koordinatensystem als Menge (x|y) der Punkte, die die lineare Gleichung
Ax+By+C=0 erfüllen, wobei die Parameter A, B und C für reelle
Zahlen stehen.
Ausgenommen ist A=B=0. In diesem
Falle gibt es entweder keinen Geradenpunkt (C< >0), oder jeder Punkt
der Ebene ist möglich (C=0).
Die lineare Gleichung Ax+By+C=0
beschreibt alle Geraden in der Ebene und ist deshalb die allgemeine
Form.
Zur nebenstehenden Geraden gehört
die Gleichung -x+2y-2=0. |
Auf dieser Seite werden die
gängigen Geradengleichungen besprochen.
Sie unterscheiden sich dadurch,
dass unterschiedliche Eigenschaften berücksichtigt werden.
Normalform
top
Die Normalform ist y=mx+b.
Herleitung
Die Gleichung Ax+By+C=0 lässt
sich nach y auflösen, wenn B ungleich Null ist: y=-(A/B)x-C/B oder
y=mx+b.
In dieser Form kann die Gleichung
als Funktionsgleichung aufgefasst werden, denn jedem x-Wert wird eindeutig
ein y-Wert zugeordnet.
Beispiel
...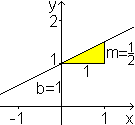 ... ... |
Aus der Geradengleichung -x+2y-2=0
wird die Normalform y=(1/2)x+1.
Die Variablen m und b findet man
in der Zeichnung.
b ist der y-Achsenabschnitt, und
m findet man in dem Steigungsdreieck, das entsteht, wenn man vom Schnittpunkt
mit der y-Achse aus 1 in x-Richtung und m in y-Richtung geht. |
Sonderfall
Ist B=0, so wird aus der allgemeinen
Gleichung Ax+By+C=0 die Verkürzung Ax+B=0 oder x=-B/A oder x=a.
...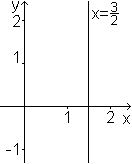 ... ... |
Die Gleichung x=a beschreibt eine Parallele zur y-Achse
im Abstand a..........................................
In diesem Falle ist es die Gerade mit x=3/2. |
Dieser Fall B=0 wird in den
folgenden Formen der Geradengleichung als Sonderfall nicht mehr erwähnt.
Achsenabschnittsform
top
Die Achsenabschnittsform ist y/a'+x/b'
= 1.
Herleitung
Sie geht durch folgende Umformung aus der allgemeinen
Geradengleichung
Ax+By+C=0 hervor.
Ax+By+C = 0
<=> Ax+By = -C
|:(-C), C<>0
<=> -Ax/C-By/C = 1
<=> x/(-C/A)+y/(-C/B)
= 1
<=> y/a'+x/b' = 1
Die Achsenabschnittsform existiert
nur, wenn C ungleich 0 ist.
Beispiel
...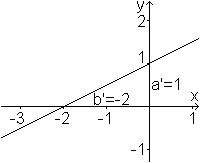 ... ... |
Aus der allgemeinen Gleichung -x+2y-2=0
wird die Achsenabschnittsform y/1+x/(-2)=1.
Die Achsenabschnittsform y/a'+x/b'=1
enthält die Schnittpunkte der Geraden mit den Achsen. |
Hessesche
Normalform (HNF) top
...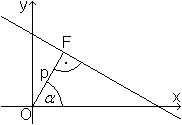 ... ... |
Die hessesche Normalform ist cos(alpha)*x+sin(alpha)*y-p=0.
Dabei sind p der Abstand der Geraden vom Nullpunkt und
alpha der Winkel zwischen der Normalen OF der Geraden und der x-Achse. |
Herleitung
...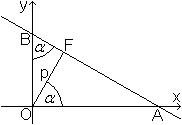 ... ... |
Oben wurde gezeigt, dass aus Ax+By+C
= 0 die Achsenabschnittsform x/(-C/A)+y/(-C/B) = 1 entstehen kann.
Dann sind in der Zeichnung OA=(-C/A)
und OB=(-C/B). -
Im Dreieck OAF und BOF stehen die Schenkel der markierten
Winkel paarweise aufeinander senkrecht und sind deshalb gleich. Damit sind
die rechtwinkligen Dreiecke OAF und BOF ähnlich. |
Man kann ablesen: cos(alpha)=OF/OA=p/(-C/A)=-Ap/C und sin(alpha)=OF/OB=-Bp/C.
Diese Terme werden eingesetzt.
cos(alpha)*x+sin(alpha)*y-p = 0
<=> -Ap/C*x-Bp/C*y-p = 0
|:p
<=> -A/C*x-B/C*y-1=0
|*(-C)
<=> Ax+By+C=0
Die Schlussrichtung ist von unten nach oben.
Man erhält konkret die
hessesche Normalform, indem man die allgemeine Gradengleichung Ax+By+C=0
mit dem Term 1/sqrt(A²+B²) multipliziert.
Wegen des Minuszeichens in x*cos(alpha)+y*sin(alpha)-p=0
und p>0 muss man zwei Fälle unterscheiden.
Ist C>0, ist mit -1/sqrt(A²+B²) zu multiplizieren:
-A/sqrt(A²+B²)x-B/sqrt(A²+B²)y-C/sqrt(A²+B²)=0.
Ist C<0, ist mit 1/sqrt(A²+B²) zu multiplizieren:
A/sqrt(A²+B²)x+B/sqrt(A²+B²)y+C/sqrt(A²+B²)=0.
Ist C=0, so spielt das Vorzeichen keine Rolle.
Die Unterscheidung nach C>0 und C<0 kann man sich ersparen,
wenn man Ax+By+C=0 mit 1/{[|C|/(-C)]*sqrt(A²+B²)} multipliziert.
Es ist zu klären, welcher
Zusammenhang zwischen cos(alpha)*x+sin(alpha)*y-p=0 und 1/sqrt(A²+B²)
besteht.
Dazu wird der Abstand p bestimmt.
... ... ... |
Die Dreiecke OAF und BOA sind ähnlich.
Damit gilt die Proportion p:OA=OB:AB oder p:(-C/A)=(-C/B):sqrt[(-C/A)²+(-C/B)²]
oder
p*sqrt[(-C/A)²+(-C/B)²]
= (-C/A)*(-C/B) oder p=[C²/(AB)]/sqrt[(C²/A²+C²/B)²]=C/[sqrt(A²+B²)].
Dann ist sqrt(A²+B²)=C/p
Oben wurde gezeigt, dass cos(alpha)=-Ap/C
und sin(alpha)=-Bp/C gelten. |
Die Terme werden eingesetzt in die Gleichung -A/sqrt(A²+B²)x-B/sqrt(A²+B²)y-C/sqrt(A²+B²)=0,
die für C>0 gilt.
-A/sqrt(A²+B²)x-B/sqrt(A²+B²)y-C/sqrt(A²+B²)
= 0
<=> -A/(C/p)*x-B/(C/p)*y-p
= 0
<=> -Ap/C*x-Bp/C*y-p = 0
<=> cos(alpha)*x+sin(alpha)*y-p = 0
Die Schlussrichtung ist wieder von unten nach oben.
Beispiel
....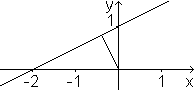 .. .. |
Die Ausgangsgerade mit -x+2y-2=0
hat die HNF
-[(1/5)sqrt(5)]*x+[(2/5)sqrt(5)]*y-[(2/5)sqrt(5)]=0
Für sie gilt p=sqrt(5)
und sin(alpha)=-[(1/5)sqrt(5)] und somit alpha=153,4°. |
Der Sinn der hesseschen Normalform erschließt
sich erst in der Anwendung.
Man kann bequem den Abstand eines Punktes von einer Geraden
bestimmen.
Zweipunkteform
top
Wird eine Gerade durch die Punkte A(x1|y1)
und B(x2|y2) festgelegt, so heißt die Geradengleichung
in Zweipunkteform (y-y1)/(x-x1)=(y2-y1)/(x2-x1).
Herleitung
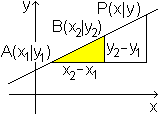 |
Die Steigung ist im gelben Dreieck abzulesen: m=(y2-y1)/(x2-x1).
Statt des festen Punktes B kann man auch den beliebigen
Geradenpunkt P nehmen.
Da gilt m=(y-y1)/(x-x1).
Damit ist (y-y1)/(x-x1)=(y2-y1)/(x2-x1),
wzbw. |
Ist x=x1, so ist
diese Gleichung auch die Geradengleichung.
Punkt-Richtungs-Form
top
Wird eine Gerade durch die Steigung
m und den Punkt A(x1|y1) festgelegt, so gilt
die Punkt-Richtungs-Form (y-y1)/(x-x1)=m.
Die Herleitung erfolgt wie bei der Zweipunkteform.
Polarform
top
...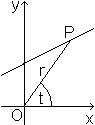 ... ... |
Für die Polarform verwendet man zur Angabe der Lage
eines Punktes P Polarkoordinaten r und t.
Das sind die Entfernung r=OP des Punktes vom Nullpunkt
O und der Winkel t zwischen einer Horizontalen und der Entfernung OP. |
Hat die Gerade die Normalform
y=mx+b, so ist die Polarform r(t)=b/[sin(t)-m*cos(t)].
Geraden parallel zur y-Achse haben die Darstellung x=a.
Das führt zu r(t)=a/cos(t).
Herleitungen
Setzt man x=r*cos(t) und y=r*sin(t) in y=mx+b ein,
so ergibt sich r*sin(t)=mr*cos(t)+b oder r(t)=b/[sin(t)-m*cos(t)].
Die Gleichung x=a führt mit x=r*cos(t) zu r=a/cos(t).
Beispiel
...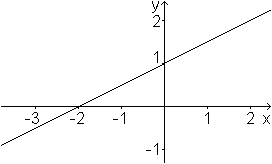 ... ... |
Die Gerade hat die Darstellung y=(1/2)x+1.
Es sind b=1 und m=1/2.
Dann ist r(t)=1/[sin(t)-(1/2)cos(t)]. |
Mehr findet man auf meiner
Seite Kurven im Polarkoordinatensystem.
Im nächsten Kapitel
werden Geraden im Raum mit Vektoren erfasst. Die beiden dort hergeleiteten
Parametergleichungen gelten in gleicher Form auch in der Ebene.
Geraden im Raum
top
Man könnte meinen, dass die
Gleichung Ax+By+C=0 zu Ax+By+Cz+D=0 verallgemeinert werden kann, um eine
Gerade im Raum zu beschreiben. Das ist falsch, denn die Gleichung beschreibt
eine Ebene im Raum.
Für eine Gerade muss man zwei
Ebenengleichungen angeben. Die Gerade ist dann die Schnittgerade beider
Ebenen.
Ax+By+Cz+D=0 /\
A'x+B'y+C'z+D'=0
Dieser Sachverhalt (zwei Koordinatengleichungen)
ergibt sich auch weiter unten aus andersartigen Überlegungen.
Beispiel
Ebene 1: x/5+y/3+z/4=1 oder 12x+20y+15z-1=0
Ebene 2: x/2,5+y/1,5=1 oder 6x+10y-15=0
Schnittgerade: 12x+20y+15z-1=0
/\ 6x+10y-15=0
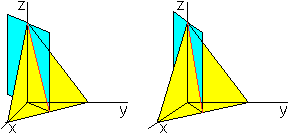
Zwei Ebenen durchdringen sich.
|
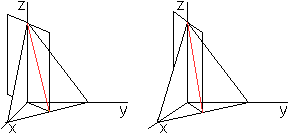
Es gibt eine Schnittgerade.
|
Die Bildpaare ermöglichen eine
3D-Sicht.
Parameterdarstellungen
der Geraden im Raum
Es ist günstig, für Probleme der Raumgeometrie
Vektoren einzusetzen.
...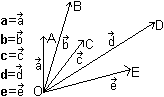 ... ... |
Es wird ein fester Punkt O im Raum festgelegt. Der Ort
aller Punkte wird durch gerichtete Strecken, also Pfeile, angegeben, die
vom Nullpunkt O ausgehen und in den Punkten enden. Sie heißen
treffend Ortsvektoren.
Man bezeichnet Vektoren mit kleinen Buchstaben, die einen
kleinen Pfeil tragen. Da ich auf meinen Seiten im wesentlichen nur den
ASCII-Code verwende, schreibe ich Vektoren als Notlösung
hier mit kleinen, fetten Buchstaben. Sie sind im englischen Sprachbereich
manchmal zu finden wie z.B. bei MathWorld.
Ich mache keinen Unterschied zwischen Pfeil und Vektor,
was streng genommen nicht korrekt ist. |
Parametergleichung
in der Zweipunkteform
...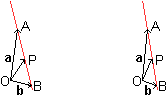 ... ... |
Eine Gerade wird durch zwei Punkte bestimmt, zum Beispiel
durch die Punkte A und B.
Folglich legen ihre Ortsvektoren a und b
die Gerade AB fest.
Den Ortsvektor p eines Geradenpunktes kann man
aus beiden Vektoren wie folgt bestimmen. |
...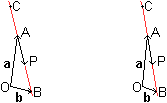 ... ... |
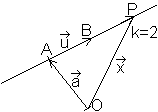
Den Ortsvektor p eines Punktes erhält man,
indem man hinter dem Vektor
a das k-fache des Differenzenvektors
b-a
hängt.
p=a+k(b-a)
So erhält man in der Zeichnung den Punkt P über
den Ortsvektor p=a+(1/2)(b-a),
da der Punkt die Strecke AB halbiert.
Der Ortsvektor von A ergibt sich über
k=0 und B über k=1. Zum neuen Punkt C
gehört der Parameter k= -1/2. |
Zu jedem Punkt der Geraden gibt es genau einen Wert für
k und umgekehrt legt jeder Wert von k genau einen Punkt fest.
Parametergleichung
in der Punkt-Richtungsform
....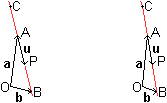 .. .. |
Es ist üblich, für
den Differenzenvektor
b-a den Richtungsvektor u einzuführen.
Dann heißt die Geradengleichung einfacher
p=a+ku.
Es gibt beliebig viele Ortsvektoren und beliebig viele
Richtungsvektoren, die eine Gerade festlegen können
und damit beliebig viele Parameterdarstellungen ein und derselben Geraden. |
Verbindung
zum kartesischen Koordinatensystem
...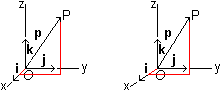 ... ... |
Ein kartesisches Koordinatensystem kennzeichnet man durch
einen Nullpunkt O und drei Grundvektoren i, j und k.
Die Grundvektoren legen die Richtung der Achsen fest.
Zu i gehört die x-Achse, zu j
die y-Achse und zu k die z-Achse.
Einen Ortsvektor p erzeugt man dadurch, dass man
passende Vielfache der Vektoren i, j und k hintereinander
hängt:
p=xi+yj+zk. In der Zeichnung ist
p=0,5i+1,5j+1,9k. |
Der Punkt P hat dann die bekannte Darstellung P(x|y|z). In
der Zeichnung ist P(0,5|1,5|1,9).
Damit ist ein Zusammenhang zwischen kartesischen Koordinaten
und Vektoren hergestellt.
Koordinatengleichungen
der Gerade im Raum
Die Darstellung von p=xi+yj+zk
wendet
man auf die Vektoren der Parametergleichung p=a+k(b-a)
an.
Es sei a=x1i+y1j+z1k,
und es sei b=x2i+y2j+z2k.
Dann ist p=a+k(b-a)
= x1i+y1j+z1k + k(x2i+y2j+z2k
- x1i-y1j-z1k)
= (x1+kx2-kx1)i + (y1+ky2-ky1)j
+
(z1+kz2-kz1)k.
Andererseits ist p=xi+yj+zk.
Damit
gilt (x1+kx2-kx1-x)i+(y1+ky2-ky1-y)j+(z1+kz2-kz1-z)k
=O.
Da die Vektoren i, j und k linear
unabhängig sind, müssen die Vorzahlen
in einer Linearkombination von i, j und k Null sein.
Das führt zu den drei Gleichungen
x1+kx2-kx1-x = 0
y1+ky2-ky1-y = 0
z1+kz2-kz1-z = 0
Umgeformt
(I) x = x1+k(x2-x1)
(II) y = y1+k(y2-y1)
(III) z = z1+k(z2-z1)
Das sind drei Gleichungen mit den vier Variablen x, y, z
und k.
Der Parameter k wird eliminiert.
Aus (I) und (II) folgt
k=(x-x1)/(x2-x1) und
k=(y-y1)/(y2-y1)
Daraus folgt
(x-x1)/(x2-x1) = (y-y1)/(y2-y1)
oder (x-x1)(y2-y1) =
(x2-x1)(y-y1)
oder (y2-y1)x-(x2-x1)y-x1y2+x2y1
=
0 |
Aus (I) und (III) folgt
k=(x-x1)/(x2-x1) und
k=(z-z1)/(z2-z1)
Daraus folgt
(x-x1)/(x2-x1) = (z-z1)/(z2-z1)
oder (x-x1)(z2-z1) =
(x2-x1)(z-z1)
oder (z2-z1)x-(x2-x1)z-x1z2+x2z1
= 0 |
Ergebnis:
Die beiden Koordinatengleichungen (y2-y1)x-(x2-x1)y-x1y2+x2y1
=
0 /\ (z2-z1)x-(x2-x1)z-x1z2+x2z1
= 0 beschreiben eine Gerade im Raum.
Man könnte auch die
Gleichung (z2-z1)y-(y2-y1)z-y1z2+y2z1
= 0 an Stelle einer Gleichung nehmen. Sie ergibt sich aus (II) und (III).
Geometrische
Deutung
Die Gleichung (y2-y1)x-(x2-x1)y-x1y2+x2y1
=
0 stellt eine Ebene im Raum dar. Da die Variable z fehlt, ist die z-Achse
parallel zur Ebene.
Die Gleichung (z2-z1)x-(x2-x1)z-x1z2+x2z1
= 0 stellt eine Ebene im Raum dar. Da die Variable y fehlt, ist die y-Achse
parallel zur Ebene.
Die Gleichung (z2-z1)y-(y2-y1)z-y1z2+y2z1
= 0 stellt eine Ebene im Raum dar. Da die Variable x fehlt, ist die
x-Achse parallel zur Ebene.
Die Gerade ist die Schnittgerade zweier dieser Ebenen.
Die Gerade kann die Schnittgerade
vieler Ebenen sein.
Jedoch sind zwei dieser hier angegebenen Gleichungen
der besonderen Ebenen eine Standarddarstellung einer Geraden im Raum.
In einer anderen Deutung
sieht man die drei Geraden auch als senkrechte Parallelprojektion der gegebenen
Geraden in die drei Hauptebenen.
Beispiel
...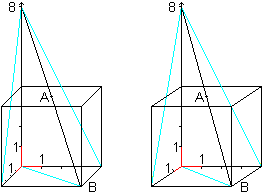 ... ... |
Gegeben sind ein Würfel
der Kantenlänge 4 und auf ihm zwei Punkte. Das sind der Mittelpunkt
A der Deckfläche mit der Darstellung A(2|2|4) und ein gegenüberliegender
Eckpunkt B mit B(4|4|0).
Gesucht sind die Projektionen der Gerade AB auf die Hauptebenen.
Für einen beliebigen
Geradenpunkt gilt p=a+k(b-a)=(2i+2j+4k)+k(2i+2j-4k).
Das führt zu den Koordinatengleichungen
(I) x=2+2k
(II) y=2+2k
(III) z=4-4k
(I)-(II) ergibt x-y=0 oder y=x.
2(II)+(III) ergibt 2y+z=8 oder z= -2y+8.
2(I)+(III) ergibt 2x+z=8 oder z= -2x+8. |
...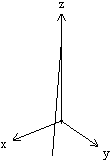 ... ...
Darstellung mit Winplot
|
Ergebnis: Die Projektionsgeraden haben die Gleichungen
y=x, z= -2x+8 und z= -2x+8.
Die Zeichnung bestätigt
die Rechnung.
Übersicht
top
Geraden in der Ebene
Allgemeine Form
General form
Ax+By+C=0 |
Normalform
Slope–intercept form
y=mx+b |
Achsenabschnittsform
Intercept form
y/a'+x/b' = 1 |
Hessesche Normalform (HNF)
Hesse standard form
-A/sqrt(A²+B²)x-B/sqrt(A²+B²)y-C/sqrt(A²+B²)=0
u.a. |
Zweipunkteform
Two-point form
(y-y1)/(x-x1)=(y2-y1)/(x2-x1) |
Punkt-Richtungs-Form
Point–slope form
(y-y1)/(x-x1)=m |
Polarform
Polar Form
r(t)=b/[sin(t)-m*cos(t)] |
Vektorgleichung
vector equation of a line
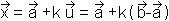 |
Geraden im Raum
Parameterdarstellung in Zweipunkteform und Parameterdarstellung
in Punktrichtungsform
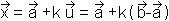
|
Zwei Koordinatengleichungen
Ax+By+Cz+D=0 /\ A'x+B'y+C'z+D'=0 |
Geradengleichung
im Internet top
Deutsch
André Mössner
Geradengleichungen
Arndt Brünner
Gerade
durch zwei Punkte finden
Friedrich Cordes
Lagebeziehung
zweier Geraden
Sarah Zigman, Jens Hillringhaus [Mathe(Pisma)]
Geradengleichungen
Wikipedia
Gerade,
Geradengleichung,
Strecke
(Geometrie),
Parameterdarstellung,
Hessesche
Normalform, Vektor,
Hilberts
Axiomensystem der euklidischen Geometrie
Englisch
Eric W. Weisstein (MathWorld)
Line,
Line
Segment,
Point-Line
Distance 3-Dimensional
Richard Parris (Freeware-Programme)
winplot
Wikipedia
Line
(geometry),
Linear
equation,
Line
segment,
Hesse
normal form, Euclidean
vector
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2009 Jürgen Köller
top |
 ...
...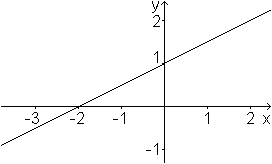 ...
...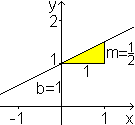 ...
...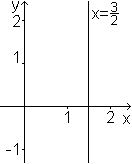 ...
...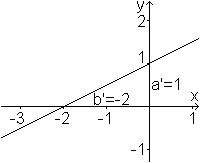 ...
... ...
... ...
...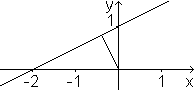 ..
..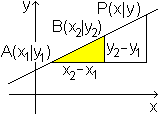
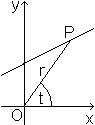 ...
...


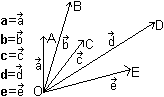 ...
...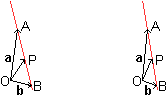 ...
...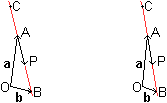 ...
...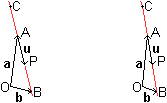 ..
..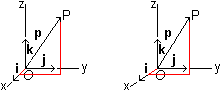 ...
... ...
... ...
...