|
Was ist mit Flussüberquerungen
gemeint?
Mit diesem Titel sind bekannte
Transportprobleme gemeint wie das vom Bauern, der Ziege, dem Wolf und dem
Korb mit Kohlköpfen, die über einen Fluss sollen.
Um dieses bekannte Rätsel der
Unterhaltungsmathematik herum gibt es mehr zum Thema Flussüberquerung.
Überquerung
eines Flusses
top
Ein Boot soll einen Fluss überqueren. Dabei sind
drei Fälle interessant.
... ... |
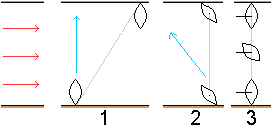1 Das Boot fährt senkrecht auf das gegenüberliegende
Ufer zu. Dabei wird es abgetrieben.
2 Das Boot fährt so gegen die Strömung, dass
es auf kürzestem Wege zum gegenüberliegenden Ufer gelangt.
3 Das Boot stellt sich quer und wird so gegen das gegenüberliegende
Ufer gedrückt. Das ist das Prinzip alter Fähren. |
Rechnung
zu Fall 1
... ... |
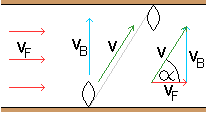Gegeben sei die Fließgeschwindigkeit des Flusses
vF und die Eigengeschwindigkeit vB eines Motorbootes.
Es überlagern sich zwei voneinander unabhängige Bewegungen.
Es gilt für die tatsächliche Geschwindigkeit
v des Bootes:
Vektor v=Vektor vF +Vektor vB
Die Beziehung wird links im Dreieck dargestellt. Es gilt
v=sqrt(vF²+vB²). |
Für den Winkel, um den das Boot abgetrieben wird, gilt
tan(alpha)=vB/vF.
Zahlenbeispiel
Gegeben: vF=3 m/s (=10,8km/h), vB=4m/s,
Flussbreite a=200m
Gesucht: v, alpha, Weg s, Fahrtzeit t
Rechnung v=sqrt(vF²+vB²)=[sqrt(9+16)]m/s=5
m/s, alpha=arc tan(4/3)=53,1°,
s=200m/(sin53.1°)=250m, t=s/v=(250m)/(5m/s)=50s
Rechnung
zu Fall 2
... ... |
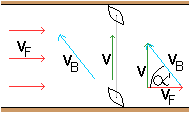Gegeben sei die Fließgeschwindigkeit des Flusses
vF und die Eigengeschwindigkeit vB eines Motorbootes.
Das Boot führt zwei voneinander unabhängige Bewegungen aus.
Es gilt für die tatsächliche Geschwindigkeit
v des Bootes:
Vektor v = Vektor vF + Vektor vB
Die Beziehung wird links im Dreieck dargestellt. Es gilt
v=sqrt(vB²-vF²). |
Für den Winkel, um den das Boot gedreht wird, gilt cos(alpha')=vF/vB.
Zahlenbeispiel
Gegeben: vF=3 m/s (=10,8km/h), vB=4m/s,
Flussbreite a=200m
Gesucht: v, alpha', Fahrtzeit t
Rechnung v=sqrt(vB²-vF²)=[sqrt(16-9)]m/s=2,6
m/s, alpha'=arc cos(3/4)=41,4°, t=s/v=200m/(2,6m/s)=76,9s
Ein Ergebnis: Der kurze Weg
in Fall 2 muss mit einer längeren Fahrtzeit gegenüber Fall 1
in Kauf genommen werden.
Anmerkungen zu Fall 3
... ...
September 2008
|
Es gibt Fähren, die benutzen die Fließgeschwindigkeit
des Flusses, um sich von Ufer zu Ufer hin und her zu bewegen. Dazu müssen
die Fähren schräg zur Flussrichtung gestellt werden.
Will man auf kürzestem Wege von Wittenberg nach Wörlitz
gelangen, muss man bei Coswig mit dieser Fähre die Elbe überqueren. |
Und wie funktioniert sie?
... ... |
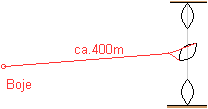Die Fähre wird von einem langen Halteseil gehalten,
das am Flussgrund befestigt und mit einer Boje hochgehalten und markiert
wird. Das Halteseil spaltet sich vor der Fähre (Y-Gierseil). Seine
Enden sind an Bug und Heck der Fähre befestigt. Die Fähre wird
schräg gestellt, indem man eine Seilwinde betätigt. Fähren
dieser Art heißen Gierseilfähren. |
Fünf
Entscheidungsprobleme ("CROSSING RIVER PROBLEMS") top
Bauer, Wolf, Ziege, Kohlkopf
Ein Bauer möchte mit einem Kahn einen Wolf, eine
Ziege und einen Kohlkopf über einen Fluss transportieren. Die
Schwierigkeit besteht darin, dass der Bauer nur eins von den Dreien mitnehmen
kann und dass die Paare (Wolf, Ziege) und (Ziege, Kohlkopf) aus verständlichen
Gründen nicht sich selbst überlassen werden dürfen.
Wie ist der Transport zu bewerkstelligen?
Eine Lösung:
7 Fahrten
Quellen:
(1) XVIII. PROPOSITIO DE HOMINE ET CAPRA ET LVPO
(2) 375 FIVE JEALOUS HUSBANDS
Mr. Softleigh und seine Familie
Mr. Softleigh und seine Familie waren in Not. Er, seine
Frau, seine beiden Söhne und sein Hund wollten einen Fluss überqueren.
Ihnen stand aber nur ein Boot mit 150 lbs. Traglast zur Verfügung.
Das war aber schon sein Gewicht und das seiner Frau. Die beiden Söhne
wogen je 75 lbs. und der Hund weniger als 75 lbs..
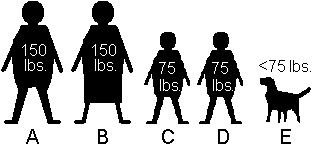Wie war der Transport zu bewerkstelligen?
Eine Lösung:
11 Fahrten
Quellen:
(1) XIX. PROPOSITIO DE VIRO ET MVLIERE PONDERANTIBVS
(2) 373 CROSSING THE STREAM
Fünf eifersüchtige Ehemänner
Bei einer Überflutung fanden
sich fünf Ehepaare plötzlich von Wasser umgeben. Es stand ihnen
nur ein drei Personen fassendes Boot zur Verfügung, um dieser ungemütlichen
Situation zu entkommen. Eine weitere Schwierigkeit bestand darin,
dass jeder Ehemann so eifersüchtig war, dass er seiner Ehefrau nicht
erlaubte, im Boot mit einem oder mehreren fremden Männern zu sein.
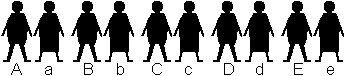
Wie war der Transport zu bewerkstelligen?
Eine Lösung:
11 Fahrten
Quellen:
(1) XVII. PROPOSITIO DE TRIBVS FRATRIBVS SINGVLAS HABENTIBVS
SORORES
(2) 375 FIVE JEALOUS HUSBANDS
Drei Missionare und drei Kannibalen
Drei Missionare und drei Kannibalen wollten einen Fluss
überqueren. Ihr Boot fasste nur zwei Personen. Das Problem bestand
zusätzlich darin, dass die Missionare aus verständlichen Gründen
auf einer Seite nicht in der Minderheit sein durften.
Wie war der Transport zu bewerkstelligen?
Eine Lösung:
11 Fahrten
Die sechs Figuren meiner
Zeichnung entstammen dem Computerspiel "Missionaries & Cannibals" (URL
unten).
Hängebrückenproblem
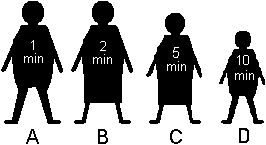
Vier Wanderer müssen eine
Hängebrücke überqueren, um zurück zu ihrem Lager zu
gelangen. Es ist Nacht und sie müssen eine Taschenlampe benutzen,
deren Batterie aber nur für 17 Minuten reicht. Die Hängebrücke
ist so schwach, dass sie nur höchstens zwei Personen trägt. Die
erste Person benötigt nur 1 min zum Überqueren, die zweite 2
Minuten und die dritte 5 Minuten und die vierte 10 Minuten (aus welchen
Gründen auch immer).
Wie war der Transport zu bewerkstelligen?
Eine Lösung:
Die fünf Überquerungen dauern 2min+2min+10min+1min+2min=17min
Quelle: Kit Logan (URL unten)
Dieses ist ein Beitrag von
Magnus Hofmayer.
Flussüberquerungen
im
Internet top
Deutsch
Chip-Online
Frogger
(Spiel zum Herunterladen) |
 |
Bernhard Berchtold (www.mathematik.ch)
Flussüberquerung
in China, Lösung
Moon
The
C64 Gamevideo Archive - Frogger
Wikipedia
Flussüberquerungsrätsel,
Propositiones
ad acuendos iuvenes, Frogger,
Königsberger
Brückenproblem
Englisch
Brain Teasers
The
Rope Bridge, Solution
John McCarthy
The
Original Missionaries and Cannibals Problem
Lulu's games
The
wolf, the goat and the cabbage (Applet)
mathcats.com
Crossing
the River (with a Wolf, a Goat, and a Cabbage)
Wikipedia
River
crossing puzzle, Fox,
goose and bag of beans puzzle, Missionaries
and cannibals problem,
Bridge
and torch problem, Propositiones
ad Acuendos Juvenes, Seven
Bridges of Königsberg
Referenzen top
(1) Alcuin of York (Albinus Flaccus Alcuinus): Propositiones
ad acuendos iuuenes (Lateinisch)
(2) Henry Ernest Dudeney: Amusements
in Mathematics, Project Gutenberg
Bei Dudeney findet man drei weitere Rätsel unter
der Überschrift CROSSING RIVER PROBLEMS:
374.—CROSSING THE RIVER AXE
376.—THE FOUR ELOPEMENTS
377.—STEALING THE CASTLE TREASURE
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2008 Jürgen Köller
top |
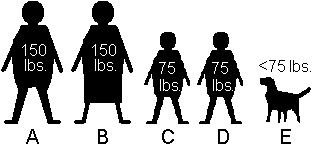